問題
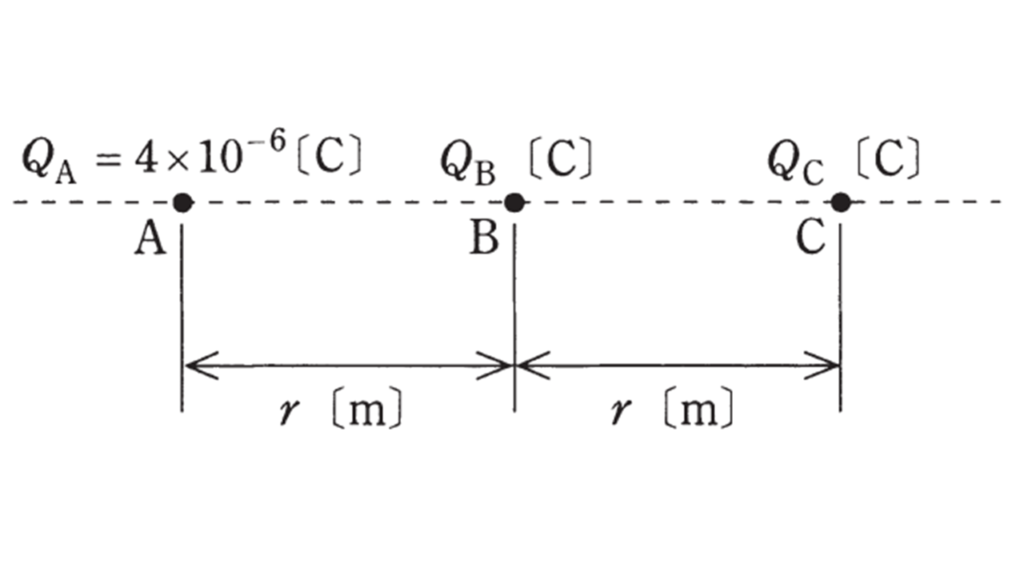
図のように,真空中の直線上に間隔 \(r\) [m] を隔てて,点 A , B , C があり,各点に電気量\( Q_A = 4×10^{−6}\) [C] , \(Q_B\) [C] , \(Q_C\) [C] の点電荷を置いた。これら三つの点電荷に働く力がそれぞれ零になった。このとき,\(Q_B\) [C] 及び\(Q_C\) [C] の値の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,真空の誘電率を\(ε_0\) [F/m] とする。
$$ \begin{array}{ccc} \ & Q_B & Q_C \\ \hline (1) & 1 \times 10^{-6} & -4 \times 10^{-6} \\ \hline (2) & -2 \times 10^{-6} & 8 \times 10^{-6} \\ \hline (3) & -1 \times 10^{-6} & 4 \times 10^{-6} \\ \hline (4) & 0 & -1 \times 10^{-6} \\ \hline (5) & -4 \times 10^{-6} & 1 \times 10^{-6} \\ \hline \end{array} $$
解説
答え:(3)
点電荷\(Q_B\)にはたらく力を求める
点電荷\(Q_B\)には,\(Q_A\)と\(Q_C\) 2つの点電荷から静電気力を受けます。点電荷\(Q_A\)から受ける力を\(F_{AB}\) [N],点電荷\(Q_C\)から受ける力を\(F_{CB}\)とすると,
\( F_{AB} = \displaystyle \frac{Q_A Q_B}{4 \pi ε_0 r^2} = \displaystyle \frac{4 \times 10^{-6} Q_B}{4 \pi ε_0 r^2} \tag{1} \)
\( F_{CB} = \displaystyle \frac{Q_C Q_B}{4 \pi ε_0 r^2} \tag{2} \)
と表すことができます。
問題文より,「…三つの点電荷に働く力がそれぞれ零になった。」と記載があるので,点電荷\(Q_B\)にはたらく2つの力\(F_{AB}\) と \(F_{CB}\)の合計はゼロとなります。
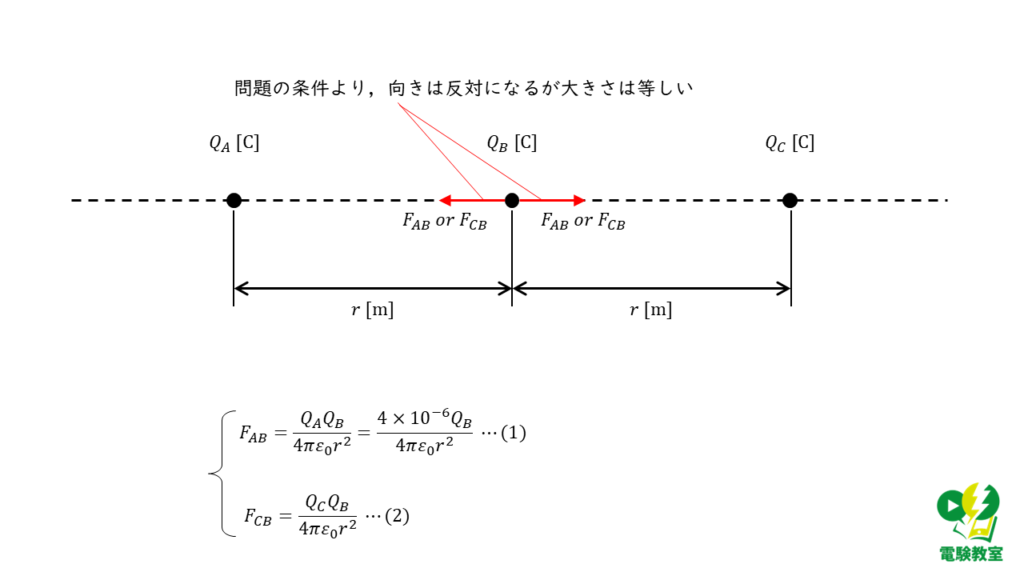
この関係を式(1)と(2)に当てはめると,
\( \begin{align} F_{AB} + F_{CB} &=0 \\ \\ F_{AB} &= -F_{CB} \\ \\ \displaystyle \frac{4 \times 10^{-6} Q_B}{4 \pi ε_0 r^2} &= -\displaystyle \frac{Q_C Q_B}{4 \pi ε_0 r^2} \\ \\ 4 \times 10^{-6} &= -Q_C \\ \\ Q_C &= -4 \times 10^{-6} \end{align} \)
と計算することができます。
この結果から\(Q_C\)の絶対値の大きさは\( 4 \times 10^{-6} \)となることが分かります。
点電荷の符号(プラス,マイナス)については,点電荷\(Q_B\)の値を求めてからでないと決定することはできません。
点電荷\(Q_C\)にはたらく力を求める
点電荷\(Q_C\)には,\(Q_A\)と\(Q_B\) 2つの点電荷から静電気力を受けます。点電荷\(Q_A\)から受ける力を\(F_{AC}\) [N],点電荷\(Q_B\)から受ける力を\(F_{BC}\)とすると,
\( F_{AC} = \displaystyle \frac{Q_A Q_C}{4 \pi ε_0 \left(2r \right)^2} = \displaystyle \frac{4 \times 10^{-6} Q_C}{4 \pi ε_0 \left(2r \right)^2} \tag{3} \)
\( F_{BC} = \displaystyle \frac{Q_B Q_C}{4 \pi ε_0 r^2} \tag{4} \)
と表すことができます。
\(Q_B\)の時と同様に,問題文より,「…三つの点電荷に働く力がそれぞれ零になった。」と記載があるので,点電荷\(Q_C\)にはたらく2つの力\(F_{AC}\) と \(F_{BC}\)の合計はゼロとなります。
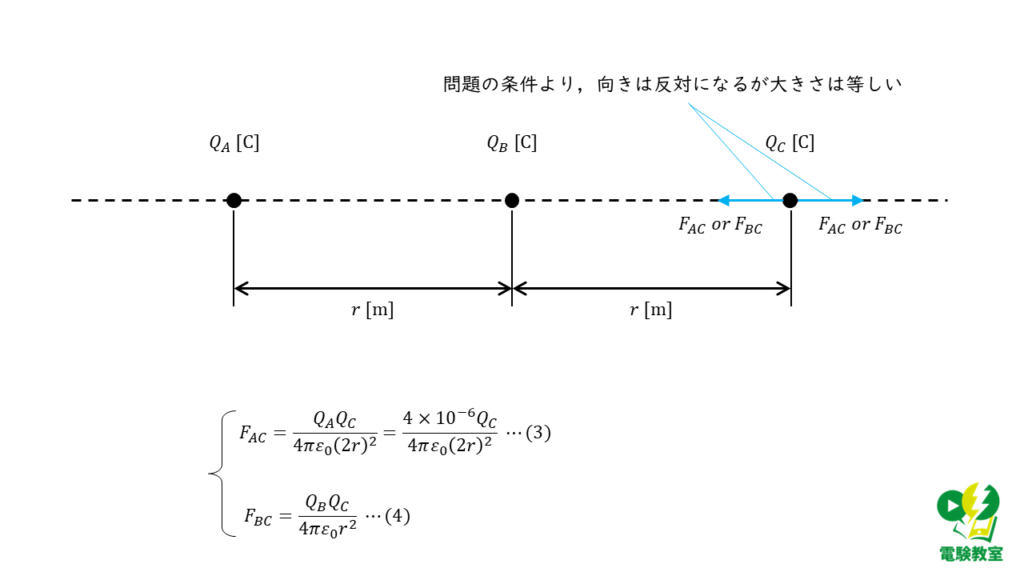
この関係を式(3)と(4)に当てはめると,
\( \begin{align} F_{AC} + F_{BC} &=0 \\ \\ F_{AC} &= -F_{BC} \\ \\ \displaystyle \frac{4 \times 10^{-6} Q_B}{4 \pi ε_0 \left(2r\right)^2} &= -\displaystyle \frac{Q_B Q_C}{4 \pi ε_0 r^2} \\ \\ \displaystyle \frac{4 \times 10^{-6}}{4} &= -Q_B \\ \\ Q_B &= -1 \times 10^{-6} \end{align} \)
以上のように計算することができます。
この結果から\(Q_B\)の絶対値の大きさは\( 1 \times 10^{-6} \)となることが分かります。
点電荷\(Q_B\)と\(Q_C\)の符号を決める
問題文より,「…三つの点電荷に働く力がそれぞれ零になった。」とあるので,この条件に当てはまる符号の組み合わせを決める必要があります。
問の選択肢より,\(Q_B\)と\(Q_C\)は必ず異なる符号になることが分かるので,それぞれのパターンについて問題の図に力の矢印を書きいれると以下の図3,4のようになります。
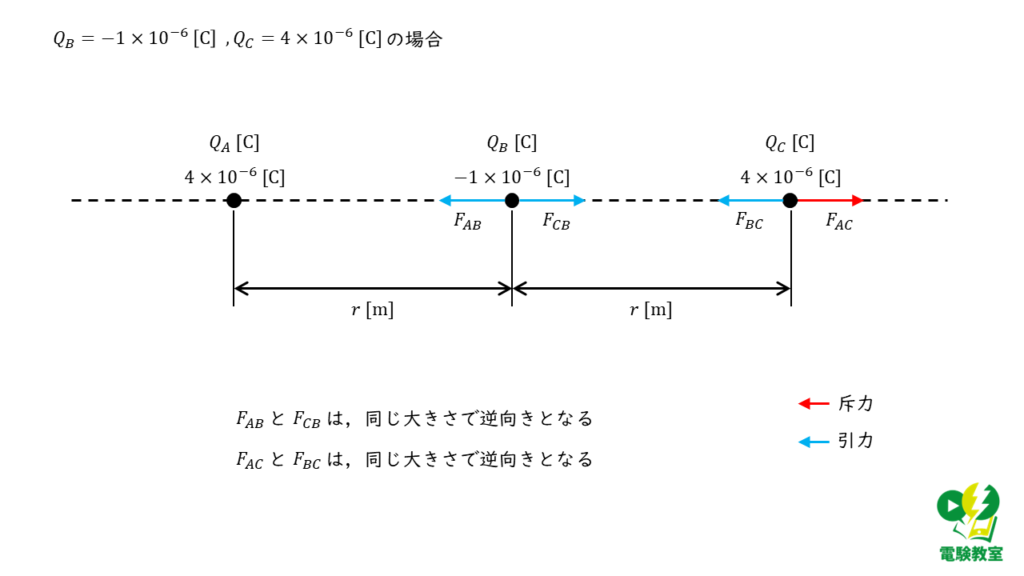
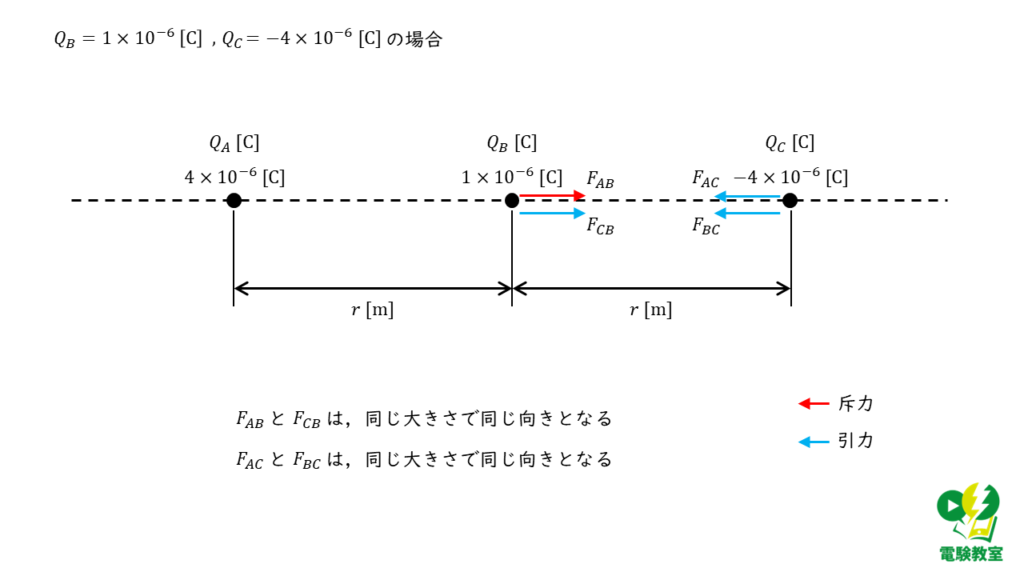
以上のことから,答えは(3)であると導くことができます。











コメント