問題
図のように,三つの平行平板コンデンサを直並列に接続した回路がある。ここで,それぞれのコンデンサの極板の形状及び面積は同じであり,極板間には同一の誘電体が満たされている。なお,コンデンサの初期電荷は零とし,端効果は無視できるものとする。
いま,端子 a-b 間に直流電圧 \(300\) [V] を加えた。このとき,次の(a)及び(b)の問に答えよ。
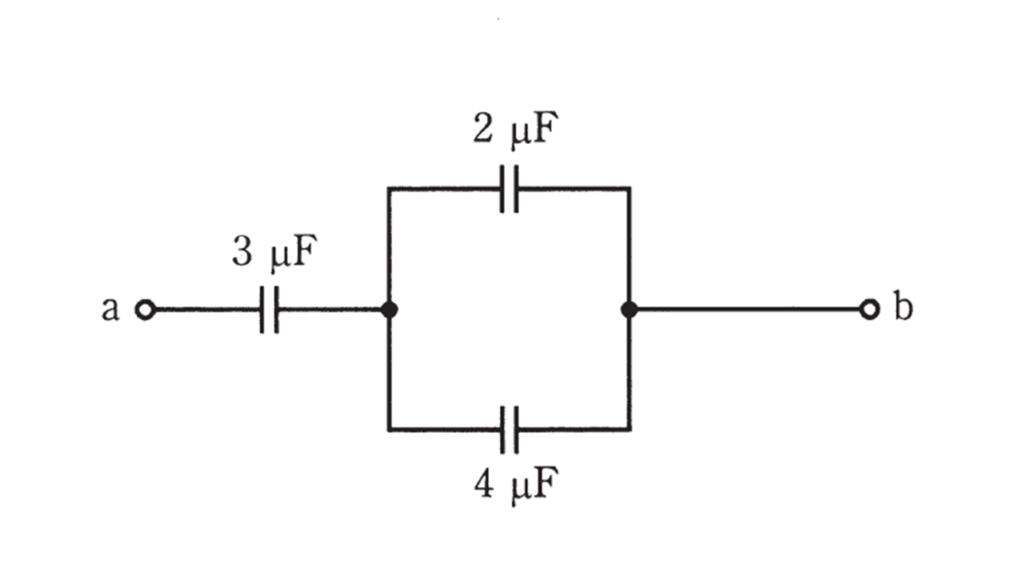
(a) 静電容量が \(4\) [μF] のコンデンサに蓄えられる電荷 \(Q\) [C] の値として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(1.2×10^{−4}\) (2) \(2×10^{−4}\) (3) \(2.4×10^{−4}\)
(4) \(3×10^{−4}\) (5) \(4×10^{−4}\)
(b) 静電容量が \(3\) [μF] のコンデンサの極板間の電界の強さは, \(4\) [μF] のコンデンサの極板間の電界の強さの何倍か。倍率として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(\displaystyle \frac{3}{4}\) (2) \(1.0\) (3) \(\displaystyle \frac{4}{3}\) (4) \(\displaystyle \frac{3}{2}\) (5) \(2.0\)
解説
答え:(a)-(5),(b)-(4)
(a) \(4\) [μF] のコンデンサに蓄えられる電荷 \(Q\) [C] の値を求める
並列接続されている部分の静電容量を計算する
問の図で並列に接続されている,2 [μF]と4 [μF]の合成容量\( C_1 \)は,
\( C_1 = 2 + 4 = 6\) [μF]
と計算することができます。したがって,問題の回路は,以下の図2のように考えることができます。
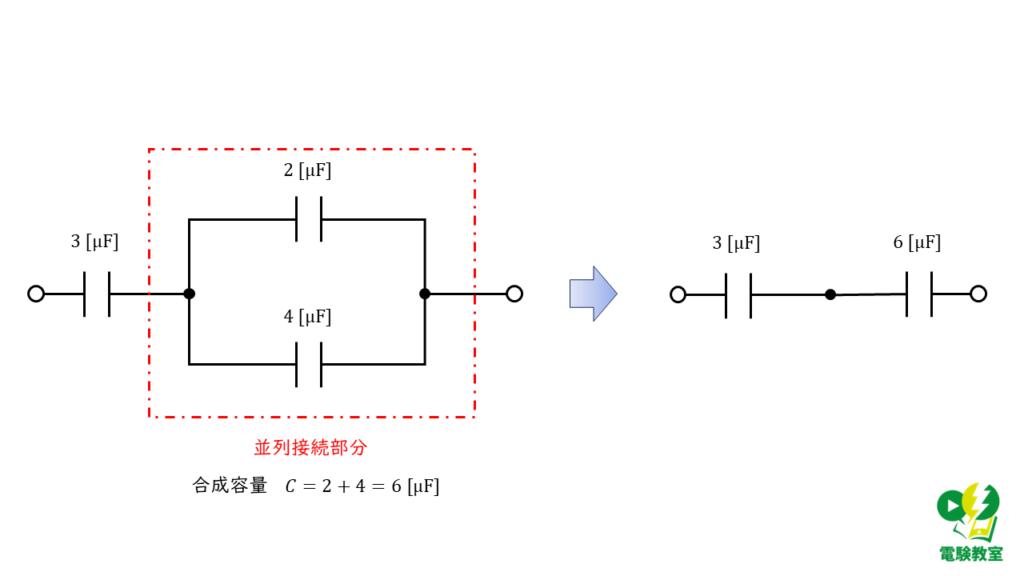
各コンデンサに印加される電圧を計算する
図2の直列に接続される2つのコンデンサに蓄えられる電荷量は等しくなります。\(3\) [μF]のコンデンサに蓄える電荷を\(Q_1\) [C], 印加される電圧を\(V_1\) [V],\(6\) [μF]のコンデンサに蓄える電荷を\(Q_2\) [C],印加される電圧を\(V_2\) [V]で表すことにします。
\( Q_1 = 3 \times 10^{-6} \times V_1 \) [C]
\( Q_2 = 6 \times 10^{-6} \times V_2 \) [C]
\( V_1 + V_2 =300 \) [V]
と表すことができ,コンデンサの特性より\( Q_1 = Q_2 \)となるので,
\( \begin{align} Q_1 &= Q_2 \\ \\ 3 \times 10^{-6} \times V_1 &= 6 \times 10^{-6} \times V_2 \\ \\ V_1 &= 2V_2 \end{align} \)
各コンデンサに印加される電圧は,\( V_1 =2V_2\)の関係にあることが分かります。
また、各コンデンサは直列に接続されているので、各コンデンサに印加される電圧の合計と電源電圧は同じ大きさとなるので、
\( \begin{align} V_1 + V_2 &= 300 \\ \\ 2V_2 + V_2 &= 300 \\ \\ V_2 &= 100 \ [\rm V ] \end{align} \)

印加される電圧\( V_2 \)と静電容量から充電される電荷量を計算する
図3より,\(4\) [μF]のコンデンサには,\( V_2 = 100\) [V]の電圧が印加されるので,蓄えられる電荷量\( Q\) [C] は,
\( Q = 4 \times 10^{-6} \times 100 = 4 \times 10^{-4} \) [C]
と計算することができます。したがって,答えは(5)となります。
(b) \(3\) [μF] のコンデンサの電界の強さが, \(4\) [μF] のコンデンサの電界の強さの何倍か計算する
\(3\) [μF] のコンデンサ, \(4\) [μF] のコンデンサに蓄えられる電荷量を求める
図3より,\(3\) [μF]に蓄えられる電荷量\(Q_1\)は,
\( Q_1 = 3 \times 10^{-6} \times 200 = 6 \times 10^{-4} \) [C]
と計算することができます。
\(4\) [μF]に蓄えられる電荷量\(Q_2\)は,(a)の答えより,
\( Q_2 = 4\times 10^{-4} \) [C]
とわかります。
各電界の大きさを求める
電界の大きさは,電気力線の密度によって求めることができるので,\(3\) [μF] のコンデンサ, \(4\) [μF] のコンデンサそれぞれの電界力線の本数を\( \psi_1 \),\( \psi_2\)で表すと,
\( \psi_1 = \displaystyle \frac{Q_1}{\varepsilon_0} = \displaystyle \frac{6 \times 10^{-4}}{\varepsilon_0} \)
\( \psi_2 = \displaystyle \frac{Q_2}{\varepsilon_0} = \displaystyle \frac{4\times 10^{-4}}{\varepsilon_0} \)
ただし,\(\varepsilon_0\) は真空中の誘電率を表す
以上のようになります。
問題文より,各コンデンサの極板間距離\( d \ \rm[m]\),極板の面積\( S \ \rm [m^2]\)は等しいので,\(3\) [μF] のコンデンサ, \(4\) [μF] のコンデンサそれぞれの電界を\( E_1 \) ,\(E_2\)で表すと以下のようになります。
\( E_1 = \displaystyle \frac{\psi_1}{S} = \displaystyle \frac{\displaystyle \frac{6 \times 10^{-4}}{\varepsilon_0}}{S} = \displaystyle \frac{6 \times 10^{-4}}{\varepsilon_0 S} \)
\( E_2 = \displaystyle \frac{\psi_2}{S} = \displaystyle \frac{\displaystyle \frac{4 \times 10^{-4}}{\varepsilon_0}}{S} = \displaystyle \frac{4 \times 10^{-4}}{\varepsilon_0 S} \)
よって、静電容量が \(3\) [μF] のコンデンサの極板間の電界の強さは, \(4\) [μF] のコンデンサの極板間の電界の強さの
\( \displaystyle \frac{E_1}{E_2} = \displaystyle \frac{\displaystyle \frac{6 \times 10^{-4}}{\varepsilon_0 S}}{\displaystyle \frac{4 \times 10^{-4}}{\varepsilon_0 S}} = \displaystyle \frac{3}{2} \)
よって、答えは(4)となります。











コメント