問題
真空中において,図に示すように,一辺の長さが \(6\) [m] の正三角形の頂点 A に \(4×10^{−9}\) [C] の正の点電荷が置かれ,頂点 B に \(−4×10^{−9}\) [C] の負の点電荷が置かれている。 正三角形の残る頂点を点 C とし,点 C より下した垂線と正三角形の辺 AB との交点を点 D として,次の(a)及び(b)に答えよ。
ただし,クーロンの法則の比例定数を \(9×10^9\) [\( \rm N⋅m^2/C^2\)] とする。
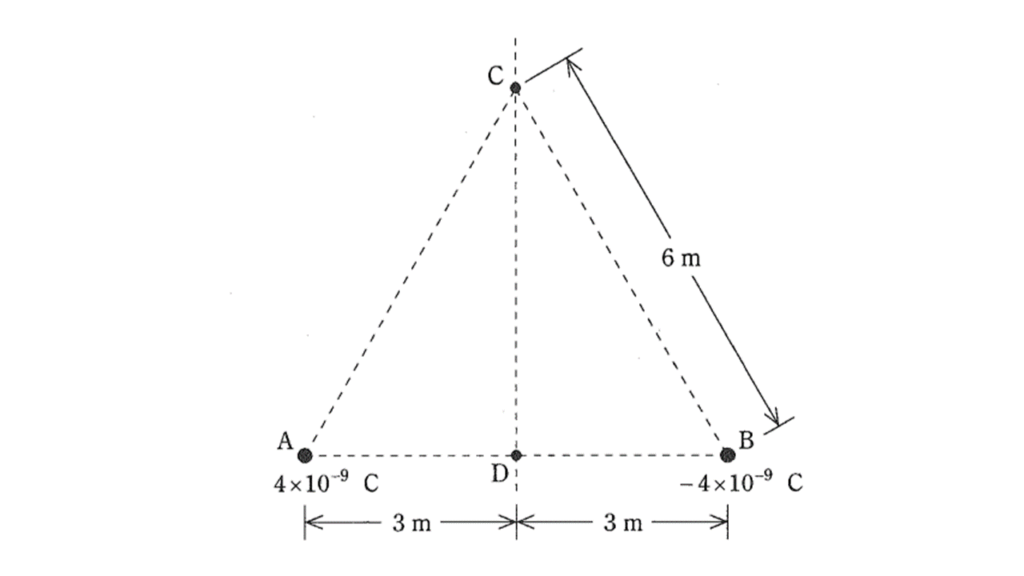
(a) まず, \(q_0\) [C] の正の点電荷を点 C に置いたときに,この正の点電荷に働く力の大きさは \(F_C\) [N] であった。 次に,この正の点電荷を点 D に移動したときに,この正の点電荷に働く力の大きさは \(F_D\) [N] であった。力の大きさの比 \(\displaystyle \frac{F_C}{F_D}\) の値として,正しいのは次のうちどれか。
(1) \(\displaystyle \frac{1}{8}\) (2) \(\displaystyle \frac{1}{4}\) (3) \(2\) (4) \(4\) (5) \(8\)
(b) 次に, \(q_0\) [C] の正の点電荷を点 D から点 C の位置に戻し,強さが \(0.5\) [V/m] の一様な電界を辺 AB に平行に点 B から点 A の向きに加えた。このとき, \(q_0\) [C] の正の点電荷に電界の向きと逆の向きに \(2×10^{−9}\) [N] の大きさの力が働いた。正の点電荷 \(q_0\) [C] の値として,正しいのは次のうちどれか。
(1) \(\displaystyle \frac{4}{3}×10^{−9}\) (2) \(2×10^{−9}\) (3) \(4×10^{−9}\)
(4) \(\displaystyle \frac{4}{3}×10^{−8}\) (5) \(2×10^{−8}\)
解説
答え:(a)-(1),(b)-(3)
(1) 力の大きさの比\( \frac{F_C}{F_D}\)について求める
電荷 \(q_0\) [C]を点Cに置いた時の力\(F_C\) [N]を求める
点Cに電荷を置いた時,A点の電荷との間の静電気力を \( F_{AC}\) ,B点の電荷との間の静電気力を \(F_{BC}\) とすると,力の大きさ\( \vert \vec{F}_{AC} \vert \) と \( \vert \vec{F}_{BC} \vert \) はそれぞれ,
\( \begin{align} F_{AC} &= \vert \vec{F}_{AC} \vert \\ \\ &= \left \vert \displaystyle \frac{4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 6^2} \right \vert \\ \\ &= \displaystyle \frac{4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 6^2} \\ \\ &= 9×10^9 \times \displaystyle \frac{4 \times 10^{-9} \times q_0}{6^2} = q_0 \end{align} \)
\( \begin{align} F_{BC} &= \vert \vec{F}_{BC} \vert \\ \\ &= \left \vert \displaystyle \frac{-4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 6^2} \right \vert \\ \\ &= \displaystyle \frac{4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 6^2} \\ \\ &= 9×10^9 \times \displaystyle \frac{4 \times 10^{-9} \times q_0}{6^2} = q_0 \end{align} \)
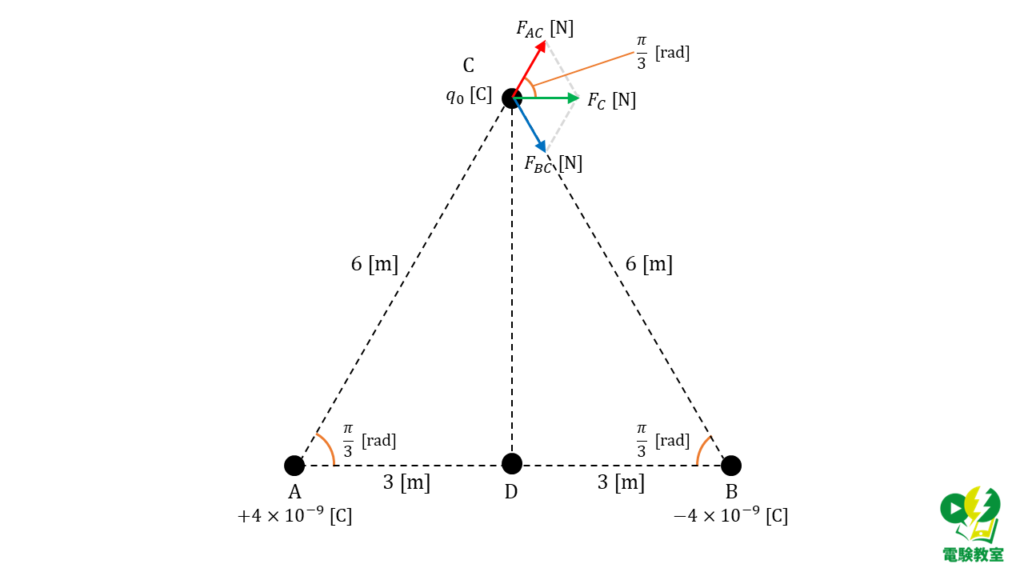
上図より,点Cに置いた場合は,はたらく力\(F_C\)はベクトルの合成によって求める必要があります。
横方向のベクトルについて
\( \begin{align} & F_{AC} \cos\displaystyle \frac{\pi}{3} + F_{BC} \cos\displaystyle \frac{\pi}{3} \\ \\ &=q_0 \times \displaystyle \frac{1}{2} + q_0 \times \displaystyle \frac{1}{2} \\ \\ &= q_0 \end{align} \)
縦方向のベクトルについて
\( \begin{align} & F_{AC} \sin \displaystyle \frac{\pi}{3} – F_{BC} \sin \displaystyle \frac{\pi}{3} \\ \\ &= q_0 \times \displaystyle \frac{\sqrt{3}}{2} – q_0 \times \displaystyle \frac{\sqrt{3}}{2} \\ \\ &= 0 \end{align} \)
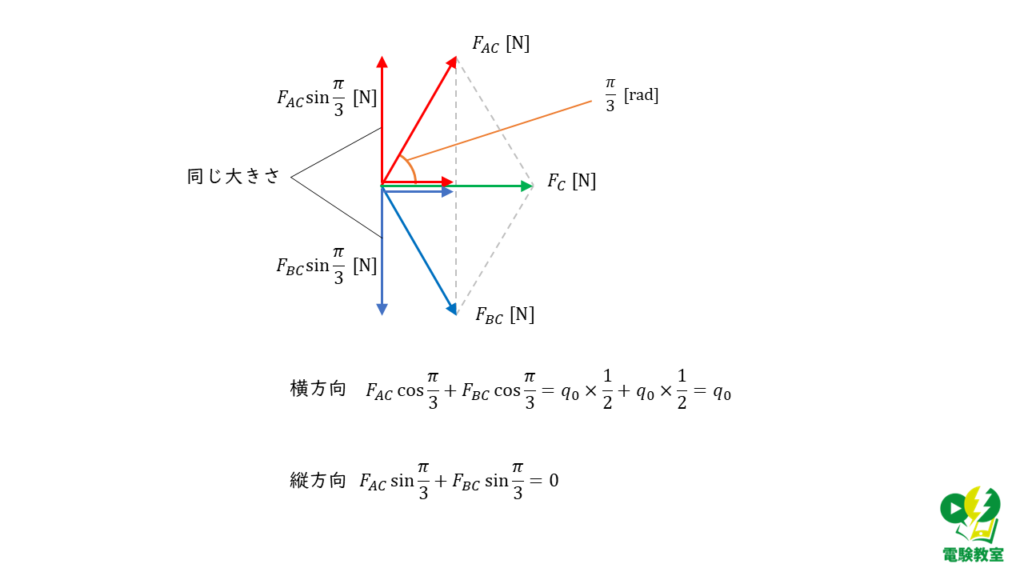
よって合成ベクトル\( F_C \) の大きさは,三平方の定理を用いて,
\( F_C = \sqrt{ \left( q_0 \right)^2 + 0^2 } = q_0 \)
電荷 \(q_0\) [C]を点Dに置いた時の力\(F_D\) [N]を求める
点Dに電荷を置いた時,A点の電荷との間の静電気力を \( F_{AD}\) ,B点の電荷との間の静電気力を \(F_{BD}\) とすると,力の大きさ\( \vert \vec{F}_{AC} \vert \) と \( \vert \vec{F}_{BC} \vert \) はそれぞれ,
\( \begin{align} F_{AD} &= \vert \vec{F}_{AD} \vert \\ \\ &= \left \vert \displaystyle \frac{4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 3^2} \right \vert \\ \\ &= \displaystyle \frac{4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 3^2} \\ \\ &= 9×10^9 \times \displaystyle \frac{4 \times 10^{-9} \times q_0}{3^2} = 4q_0 \end{align} \)
\( \begin{align} F_{BD} &= \vert \vec{F}_{BD} \vert \\ \\ &= \left \vert \displaystyle \frac{-4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 3^2} \right \vert \\ \\ &= \displaystyle \frac{4 \times 10^{-9} \times q_0}{4 \pi \varepsilon_0 3^2} \\ \\ &= 9×10^9 \times \displaystyle \frac{4 \times 10^{-9} \times q_0}{3^2} = 4q_0 \end{align} \)

点A,B,Dは,一直線上に並んでいるので,点Dに置いた電荷にはたらく力の大きさは,
\( F_D = F_{AD} + F_{BD} = 4q_0 + 4q_0 = 8q_0\)
力の大きさの比\( \displaystyle \frac{F_C}{F_D}\)について求める
以上の計算結果から,力の大きさの比\( \displaystyle \frac{F_C}{F_D}\)は,
\( \displaystyle \frac{F_C}{F_D} = \displaystyle \frac{ q_0 }{8q_0} = \displaystyle \frac{1}{8} \)
よって答えは,(1)になります。
(b) 正の点電荷 \(q_0\) [C] の値を求める
電界\(E\) [V/m] 中に電荷\( q\) [C] を置いた時にはたらく力の大きさ \(F\) [N] は,
\( F = E \times q\)
で求めることができます。よって,問の条件を図に表すと以下のようになっていることが分かります。
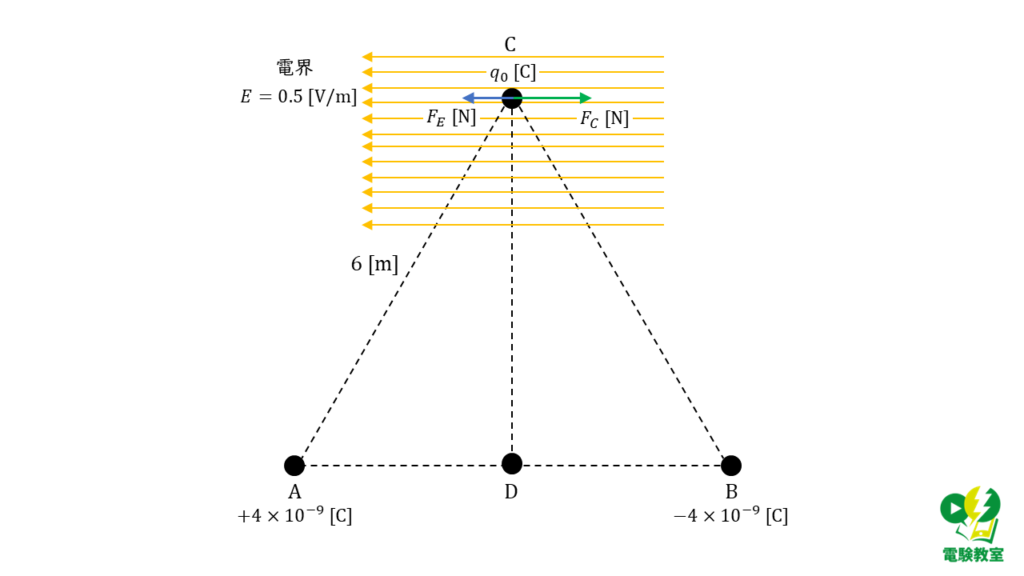
問題文には,「… \(q_0\) [C] の正の点電荷に電界の向きと逆の向きに \(2×10^{−9}\) [N] の大きさの力が働いた」と記載があるので,図より,
\( \begin{align} F_C – F_E &= 2 \times 10^{-9} \\ \\ q_0 \ – \ \left(0.5 \times q_0 \right) &= 2 \times 10^{-9} \\ \\ 0.5q_0 &= 2 \times 10^{-9} \\ \\ q_0 &= 4 \times 10^{-9} \end{align} \)
よって答えは,(3)となります。











コメント