問題
電極板面積と電極板間隔が共に \(S \ [\rm m^2]\) と \(d \ [\rm m]\) で,一方は比誘電率が \(\varepsilon_{r1} \) の誘電体からなる平行平板コンデンサ\(C_1\)と,他方は比誘電率が \( \varepsilon_{r2} \) の誘電体からなる平行平板コンデンサ\(C_2\)がある。いま,これらを図のように並列に接続し,端子 A,B 間に直流電圧 \( V_0 \ [\rm V]\) を加えた。このとき,コンデンサ\(C_1\)の電極板間の電界の強さを \(E_1 \ \rm [V/m] \) ,電束密度を \(D_1 \ \rm[C/m^2]\) ,また,コンデンサ\(C_2\)の電極板間の電界の強さを \(E_2 \ \rm [V/m] \) ,電束密度を \(D_2 \ \rm[C/m^2]\) とする。両コンデンサの電界の強さ \(E_1 \ \rm[V/m]\) と\( E_2 \ \rm[V/m] \)はそれぞれ \( \fbox { (ア) } \) であり,電束密度 \(D_1 \ \rm[C/m^2]\) と \(D_2 \ \rm[C/m^2]\)はそれぞれ \( \fbox { (イ) } \) である。したがって,コンデンサ\( C_1\)に蓄えられる電荷を \(Q_1 \ \rm[C] \) ,コンデンサ\(C_2\)に蓄えられる電荷を \(Q_2\ \rm[C]\)とすると,それらはそれぞれ \( \fbox { (ウ) } \) となる。
ただし,電極板の厚さ及びコンデンサの端効果は,無視できるものとする。また,真空中の誘電率を \(\varepsilon_0 \ \rm[F/m]\) とする。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる式として,正しいものを組み合わせたのは次のうちのどれか。
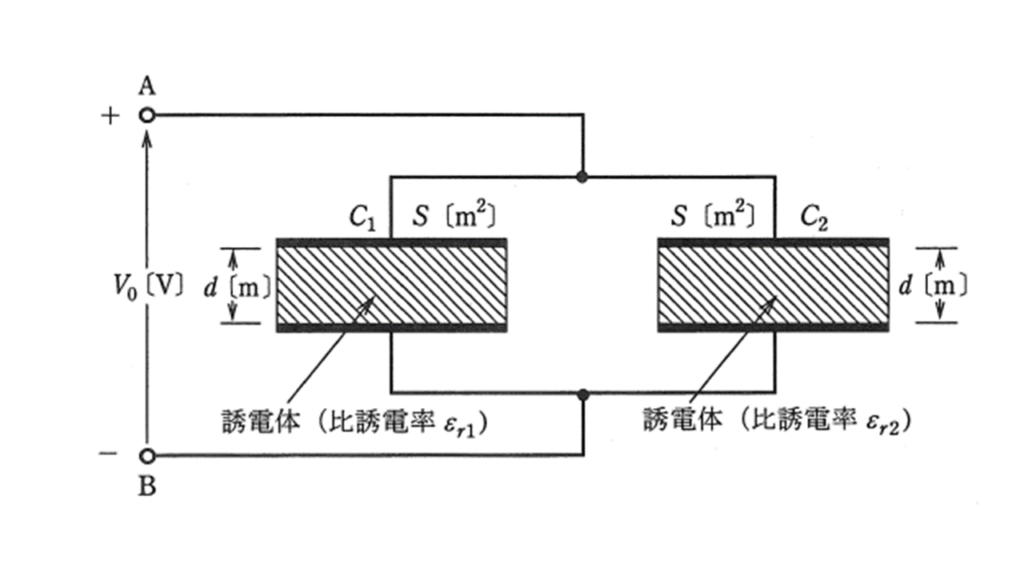
$$ \begin{array}{cccc} \ &(ア)&(イ)&(ウ)\\ \hline & E_1 = \displaystyle \frac{\varepsilon_{r1}}{d} V_0 &D_1 = \displaystyle \frac{\varepsilon_{r1}}{d}SV_0 & Q_1 = \displaystyle \frac{\varepsilon_0\varepsilon_{r1}}{d}SV_0 \\ (1)\\ &E_2= \displaystyle \frac{\varepsilon_{r2}}{d}V_0 & D_2 = \displaystyle \frac{\varepsilon_{r2}}{d}SV_0 & Q_2 = \displaystyle \frac{\varepsilon_0\varepsilon_{r2}}{d}SV_0 \\ \hline & E_1 = \displaystyle \frac{\varepsilon_{r1}}{d} V_0 &D_1 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r1}}{d}V_0 & Q_1 = \displaystyle \frac{\varepsilon_0\varepsilon_{r1}}{d}SV_0 \\ (2)\\ &E_2= \displaystyle \frac{\varepsilon_{r2}}{d}V_0 & D_2 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r2}}{d}V_0 & Q_2 = \displaystyle \frac{\varepsilon_0\varepsilon_{r2}}{d}SV_0 \\ \hline & E_1 = \displaystyle \frac{V_0}{d} &D_1 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r1}}{d}SV_0 & Q_1 = \displaystyle \frac{\varepsilon_0\varepsilon_{r1}}{d}V_0 \\ (3)\\ &E_2= \displaystyle \frac{V_0}{d} & D_2 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r2}}{d}SV_0 & Q_2 = \displaystyle \frac{\varepsilon_0\varepsilon_{r2}}{d}V_0 \\ \hline & E_1 = \displaystyle \frac{V_0}{d} &D_1 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r1}}{d}V_0 & Q_1 = \displaystyle \frac{\varepsilon_0\varepsilon_{r1}}{d}SV_0 \\ (4)\\ &E_2= \displaystyle \frac{V_0}{d} & D_2 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r2}}{d}V_0 & Q_2 = \displaystyle \frac{\varepsilon_0\varepsilon_{r2}}{d}SV_0 \\ \hline & E_1 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r1}}{d}SV_0 &D_1 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r1}}{d}V_0 & Q_1 = \displaystyle \frac{\varepsilon_0}{d}SV_0 \\ (5)\\ &E_2= \displaystyle \frac{\varepsilon_0 \varepsilon_{r2}}{d}SV_0 & D_2 = \displaystyle \frac{\varepsilon_0 \varepsilon_{r2}}{d}V_0 & Q_2 = \displaystyle \frac{\varepsilon_0}{d}SV_0 \\ \hline \end{array} $$
解説
答え:(4)
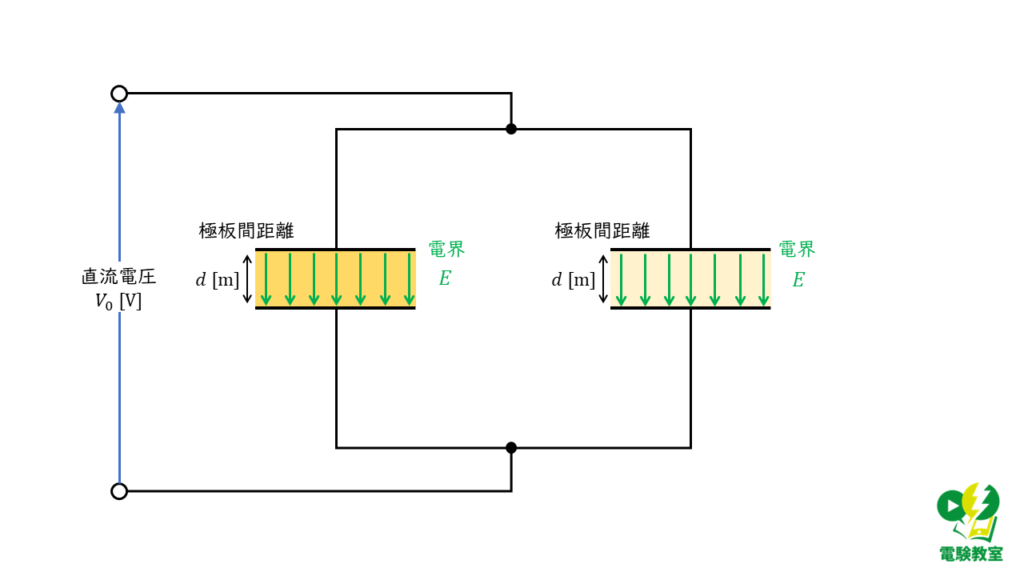
(ア) 電界の強さを求める
電圧が \(V \ \rm [V]\) の電源に接続されたコンデンサの内部電界の大きさ \(E \ \rm[V/m]\)は,極板間距離を \(d\ \rm[m]\)とすると,
\( E = \displaystyle \frac{V}{d} \)
で表すことができ,極板間の距離と電源電圧の大きさにのみ依存することが分かります。
したがって,直流電圧 \( V_0 \ \rm[V]\) と接続された並列接続の2つのコンデンサ内部の電界 \(E_1\) 及び \(E_2\)は,
\( E_1 = \displaystyle \frac{V_0}{d} \)
\( E_2 = \displaystyle \frac{V_0}{d} \)
となります。
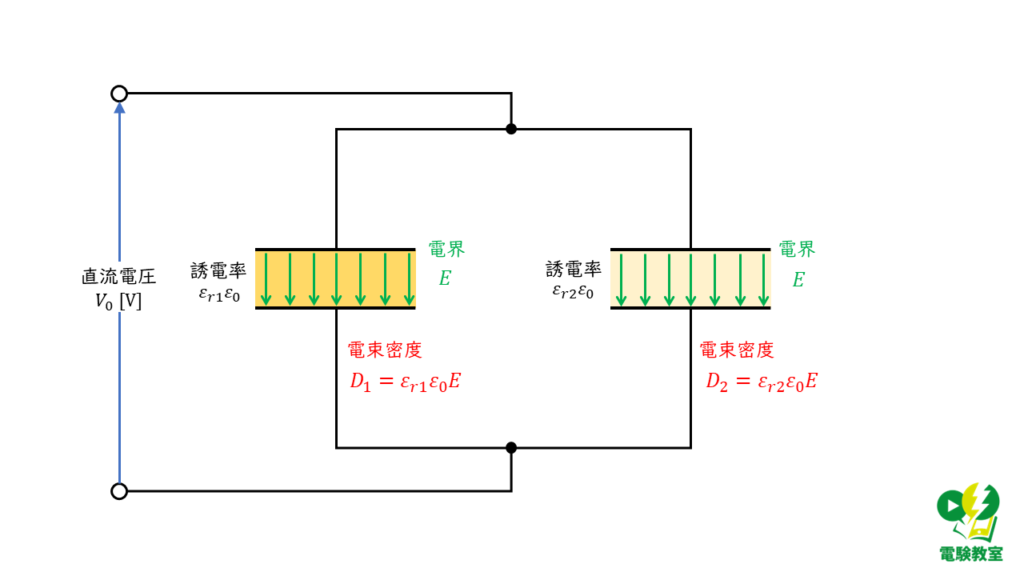
(イ) 電束密度の大きさを求める
電束密度 \(D\ \rm[C/m^2]\) と電界 \(E\ \rm[V/m]\) は誘電率を \(\varepsilon\ \rm [F/m]) とすると次の式で表すことができます。
\( D = \varepsilon \times E \)
したがって,コンデンサ \(C_1\) 及び \(C_2\) の電束密度 \( D_1\) ,\(D_2\) は,
\( \begin{align} D_1 &= \varepsilon_0 \varepsilon_{r1} \times E_1 \\ \\ & = \varepsilon_0 \varepsilon_{r1} \displaystyle \frac{V_0}{d} \end{align} \)
\( \begin{align} D_2 &= \varepsilon_0 \varepsilon_{r2} \times E_2 \\ \\ & = \varepsilon_0 \varepsilon_{r2} \displaystyle \frac{V_0}{d} \end{align} \)
と求めることができます。
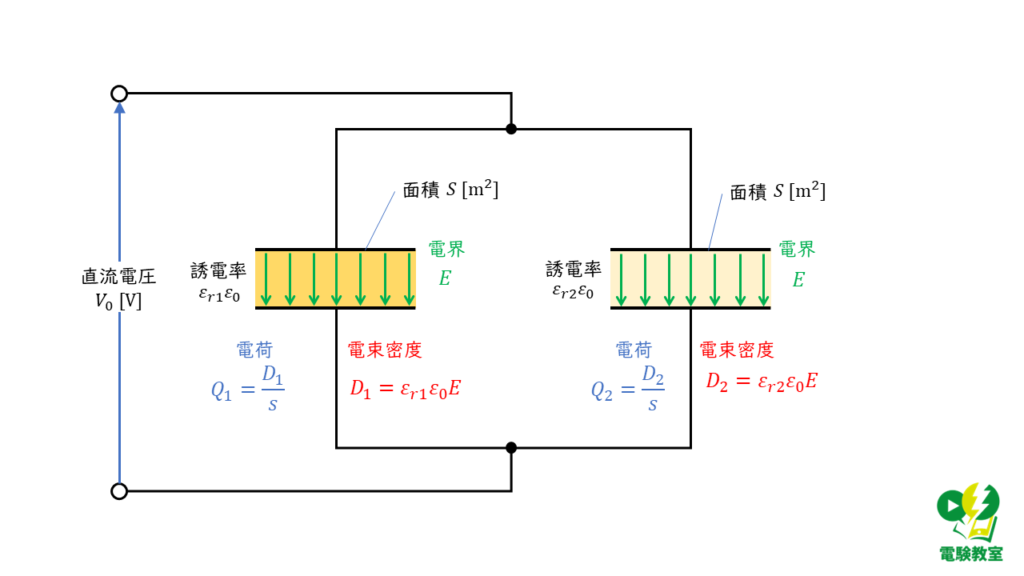
(ウ) コンデンサに蓄えられる電荷を求める
電荷 \(Q \ \rm[C]\) の大きさは,電束の本数と同じになる決まりがあります。
また,電束は(イ)で求めた電束密度と,面積 \(S \ \rm[m^2]\) を用いて,次の関係式で表すことができます。
\( 電束密度 = \displaystyle \frac{電束}{面積} \)
したがって,コンデンサ\(C_1\) ,\(C_2\) に蓄えられる電荷 \(Q_1 \) ,\(Q_2\) は,
\( Q_1 = D_1 \times S = \varepsilon_0 \varepsilon_{r1} \displaystyle \frac{SV_0}{d} \)
\( Q_2 = D_2 \times S = \varepsilon_0 \varepsilon_{r2} \displaystyle \frac{SV_0}{d} \)
と表すことができます。
以上の結果から,答えは(4)となります。











コメント