【過去問解説】R4年上期理論　問3　環状コイルのインダクタンスに関する問題

問題

図のような環状鉄心に巻かれたコイルがある。
図の環状コイルについて，
・端子 1−2 間の自己インダクタンスを測定したところ， \(40\) mH であった。
・端子 3−4 間の自己インダクタンスを測定したところ， \(10\) mH であった。
・端子 2 と 3 を接続した状態で端子 1−4 間のインダクタンスを測定したところ， \(86\) mH であった。

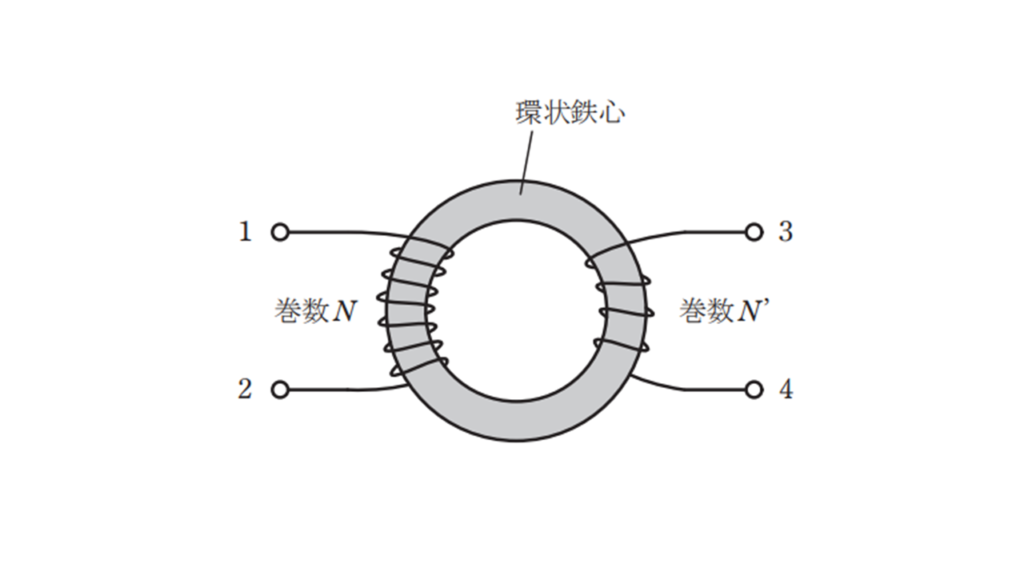
このとき，端子 1−2 間のコイルと端子 3−4 間のコイルとの間の結合係数 \(k\) の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　 \(0.81\)　(2)　 \(0.90\)　(3)　 \(0.95\)　(4)　 \(0.98\)　(5)　 \(1.8\)

解説

答え：(2)

相互インダクタンスを求める

コイル1の自己インダクタンスを \(L_1\) ，コイル2の自己インダクタンスを \(L_2\) ，相互インダクタンスを \(M\) ，2つのコイルの結合係数を \(k\) で表すとすると，以下の関係式が成り立ちます。

\( M = k \sqrt{L_1 L_2} \)

（ただし、\( 0 ≦ k ≦ 1\) ）

この式に，問題文の条件，\( L_{12} = 40\) ，\(L_{34} = 10 \) ，を代入すると結合係数は，

\( \begin{align} M &= k \sqrt{ L_{12} L_{34} } \\ \\ &= k \sqrt{ 40 \times 10 } \\ \\ &= 20k \end{align} \)

和同接続の公式に各値を代入し，結合係数を求める

端子 2 と 3 を接続した状態は，コイルに電流を流すとそれぞれのコイルが作る磁界の向きが同じ方向になるため，和動接続になることが分かります。

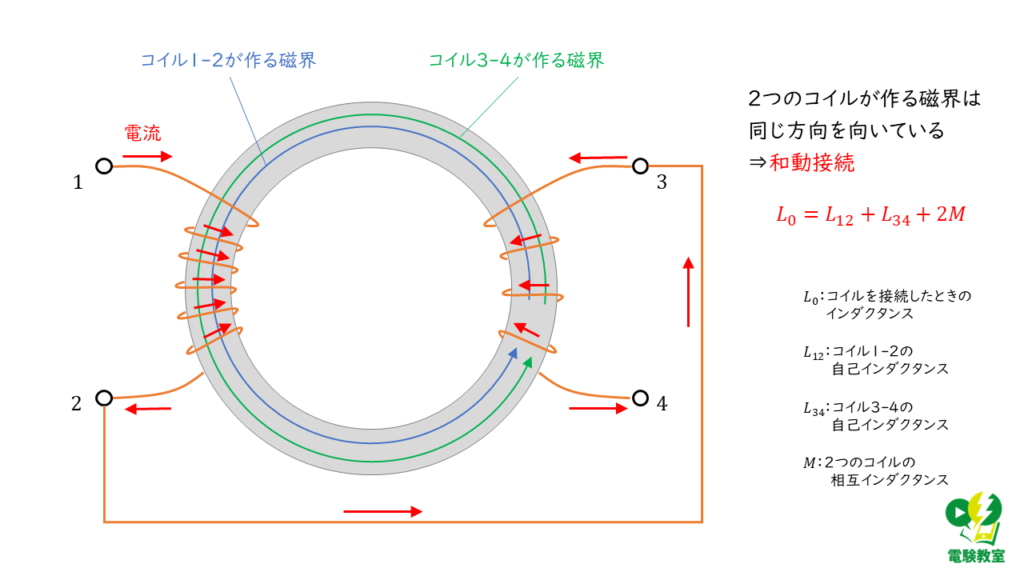
和動接続されたコイルのインダクタンス \( L_0 \) は，

\( L_0 = L_1 + L_2 + 2M \)

で表すことができます。問の条件，\( L_{12} = 40\) ，\(L_{34} = 10 \) ，\( L_0 = 86\) ，\( M = 20k \) を代入し計算すると，

\( \begin{align} L_0 &= L_{12} + L_{34} +2M \\ \\ 86 &= 40 + 10 +2\times 20k \\ \\ 40k &= 86-50 \\ \\ 40k &= 36 \\ \\ k &= 0.9 \end{align} \)

よって答えは(2)と求めることができます。