問題
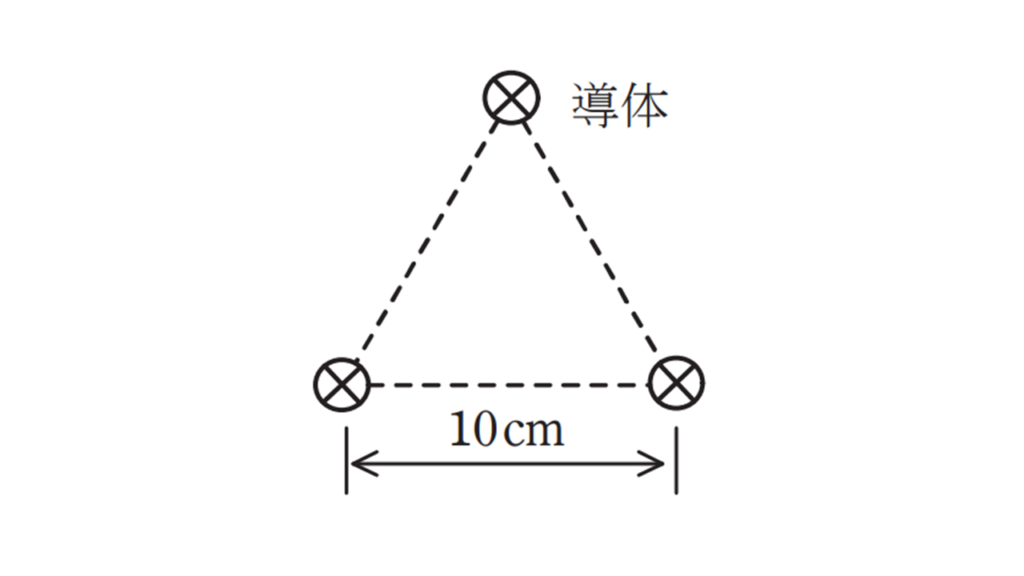
図のように,無限に長い 3 本の直線状導体が真空中に \(10\) cm の間隔で正三角形の頂点の位置に置かれている。 3 本の導体にそれぞれ \(7\) A の直流電流を同一方向に流したとき,各導体 \(1\) m 当たりに働く力の大きさ \(F_0\) の値 [N/m] として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,無限に長い 2 本の直線状導体を \(r\) [m] 離して平行に置き, 2 本の導体にそれぞれ \(I\) [A] の直流電流を同一方向に流した場合,各導体 \(1\) m 当たりに働く力の大きさ \(F\) の値 [N/m] は,次式で与えられるものとする。
\( F = \displaystyle \frac{2I^2}{r} \times 10^{-7} \)
(1) \(0\) (2) \(9.80×10^{−5}\) (3) \(1.70×10^{−4}\) (4) \(1.96×10^{−4}\) (5) \(2.94×10^{−4}\)
解説
答え:(3)
直線状にある導体間に働く力の大きさを求める
問題の文より,無限に長い 2 本の直線状導体を \(r\) [m] 離して平行に置き, 2 本の導体にそれぞれ \(I\) [A] の直流電流を同一方向に流した場合,各導体 \(1\) m 当たりに働く力の大きさ \(F\) は,
\( F = \displaystyle \frac{2I^2}{r} \times 10^{-7} \)
で計算することができます。
この式に問題の条件,導体間の距離 \(r = 0.1 \ \rm m\),直流電流の大きさ \( I = 7\ \rm A\) を代入すると,
\( F = \displaystyle \frac{2 \times 7^2}{0.1} \times 10 ^{-7} = 9.8 \times 10 ^{-5} \)
と求めることができます。
力のベクトルを図に書き入れる
3つの直線状導体は,正三角形の頂点の位置に置かれているので,電磁力のベクトルを書きいれると下図のようになります。
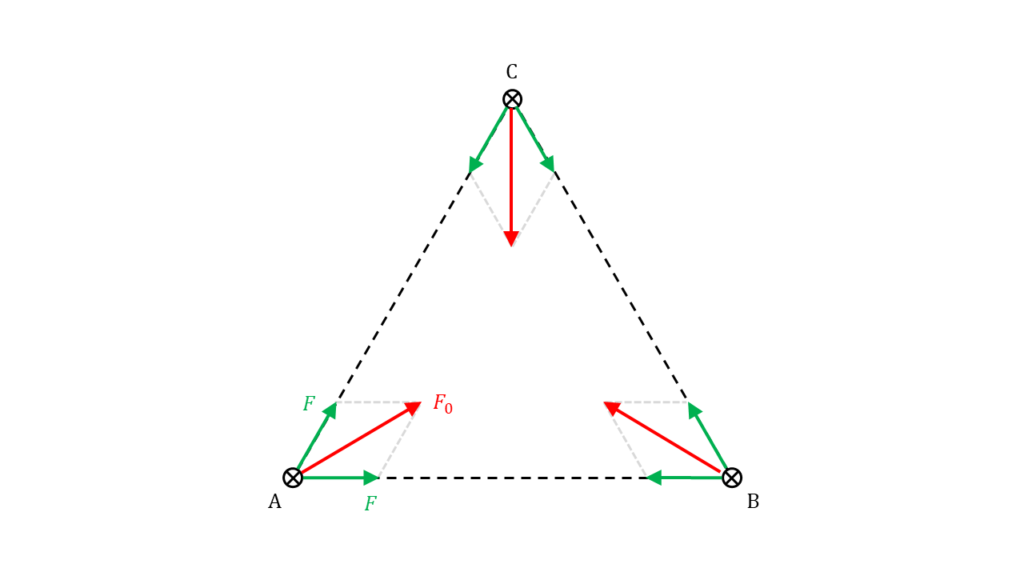
1つの導体に働く力 \(F_0\) は,2つ導体から受ける電磁力 \(F\) の合計になることが分かります。
導体に働く力 \(F_0\) を求める
導体に働く力 \(F_0\) は,2力の合成によって求めることができるため,力のベクトルの合成で考えることができます。
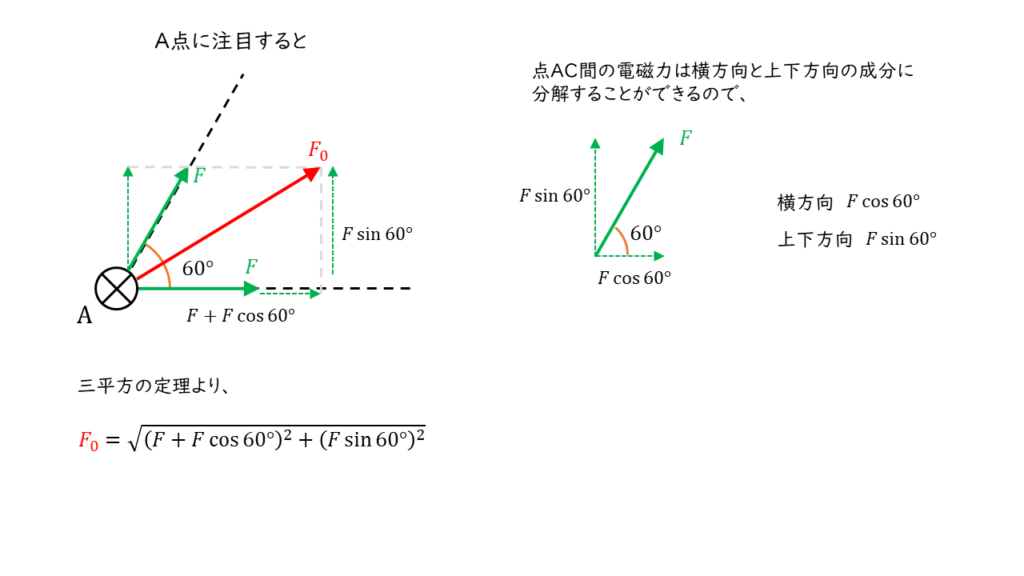
図1のように,各頂点をA,B,Cとすると,A点に置かれた導体に働く力は,
横方向
\( \begin{align} F_x &= F_{AB} + F_{AC} \cos \displaystyle \frac{\pi}{3} \\ \\ &= 9.8 \times 10 ^{-5} + 9.8 \times 10 ^{-5} \times \displaystyle \frac{1}{2} \\ \\ &= \displaystyle \frac{3}{2} \times 9.8 \times 10 ^{-5} \end{align} \)
上下方向
\( \begin{align} F_y &= F_{AC} \sin \displaystyle \frac{\pi}{3} \\ \\ &= 9.8 \times 10 ^{-5} \times \displaystyle \frac{\sqrt{3}}{2} \end{align} \)
したがって、合力 \(F_0\) [N/m]は,
\( \begin{align} F_0 &= \sqrt{ \left( F_x \right) ^2 + \left( F_y \right) ^2} \\ \\ &= \sqrt{ \left( \displaystyle \frac{3}{2} \times 9.8 \times 10 ^{-5} \right) ^2 + \left( \displaystyle \frac{\sqrt{3}}{2} \times 9.8 \times 10 ^{-5} \right) ^2} \\ \\ &= \sqrt{ \left( 9.8 \times 10 ^{-5} \right) ^2 \times \left( \displaystyle \frac{3^2}{2^2} + \displaystyle \frac{\left( \sqrt{3} \right) ^2}{2^2} \right) } \\ \\ &= 9.8 \times 10 ^{-5} \times \sqrt{ \displaystyle \frac{3+9}{4} } \\ \\ &= 9.8 \times 10 ^{-5} \times \sqrt{ 3 } \\ \\ &= 1.697 \times 10^{-4} \approx 1.7 \times 10^{-4} \end{align} \)
よって答えは(3)になります。











コメント