問題
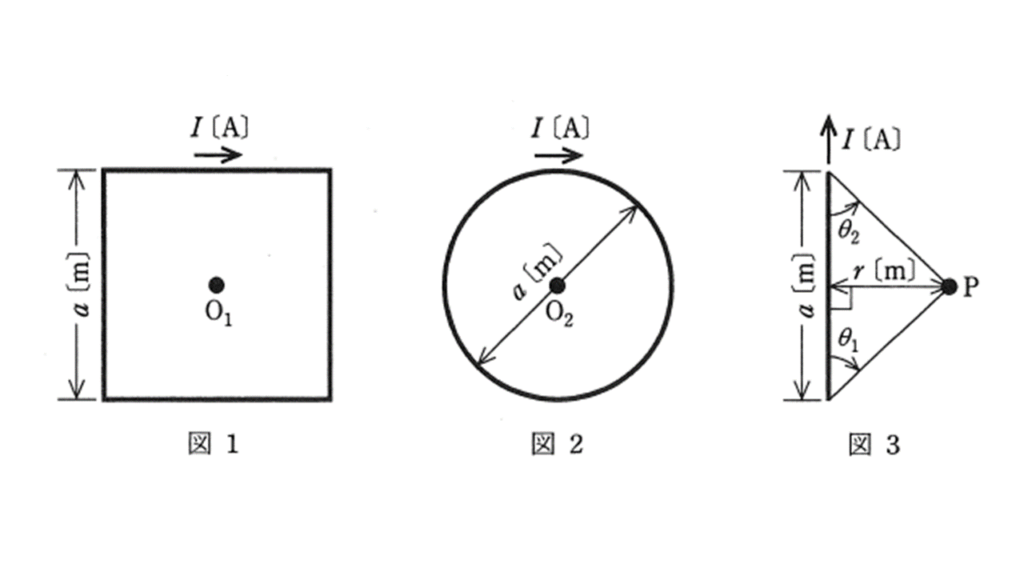
図1のように, \(1\) 辺の長さが \(a\ \rm[m]\) の正方形のコイル(巻数: \(1\) )に直流電流 \(I\ \rm[A]\) が流れているときの中心点 \(\rm O_1\) の磁界の大きさを \(H_1\ \rm[A/m]\) とする。また,図2のように,直径 \(a\ \rm[m]\) の円形のコイル(巻数: \(1\) )に直流電流 \(I\ \rm[A]\) が流れているときの中心点 \(\rm O_2\) の磁界の大きさを \(H_2\ \rm[A/m]\) とする。このとき,磁界の大きさの比 \(\displaystyle \frac{H_1}{H_2}\) の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,中心点 \(\rm O_1\) , \(\rm O_2\) はそれぞれ正方形のコイル,円形のコイルと同一平面上にあるものとする。
参考までに,図3のように,長さ \(a\ \rm [m]\) の直線導体に直流電流 \(I\ \rm[A]\) が流れているとき,導体から距離 \(r\ \rm[m]\) 離れた点 \(\rm P\) における磁界の大きさ \(H\ \rm[A/m]\) は, \(H = \displaystyle \frac{I}{4 \pi r} \left(\cos\theta_1 + \cos\theta_2 \right) \) で求められる(角度 \(\theta_1\) と \(\theta_2\) の定義は図参照)。
(1) \(0.45\) (2) \(0.90\) (3) \(1.00\) (4) \(1.11\) (5) \(2.22\)
解説
答え:(2)
正方形コイルの作る磁界 \(H_1\) の大きさを求める
図1の正方形のコイルに,図3の条件をあてはめると,以下のように考えることができます。
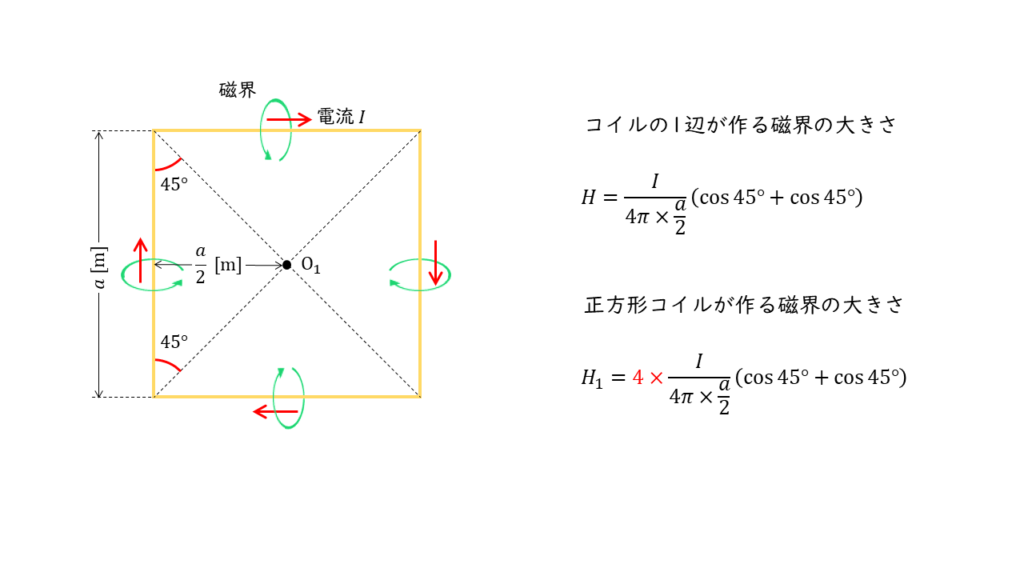
中心点 \(\rm O_1\) までの距離は \(\displaystyle \frac{a}{2}\) ,角度 \(theta_1\) ,\(theta_2\) はともに \(45°\)であるから,正方形の1辺が中心点に作る磁界 \(H\) の大きさは,
\( \begin{align} H &= \displaystyle \frac{I}{4 \pi \times \displaystyle \frac{a}{2}} \left( \cos 45° + \cos 45° \right) \\ \\ &= \displaystyle \frac{I}{2 \pi a} \left( \displaystyle \frac{\sqrt{2}}{2} + \displaystyle \frac{\sqrt{2}}{2} \right) \\ \\ &= \displaystyle \frac{\sqrt{2}I}{2 \pi a} \end{align} \)
と計算できます。正方形のコイルのため,磁界を作るコイル辺は4つと考えることができるので,磁界 \(H_1\) の大きさは,
\( \begin{align} H_1 &= H \times 4 \\ &= \displaystyle \frac{\sqrt{2}I}{2 \pi a} \times 4 \\ \\ &= \displaystyle \frac{2\sqrt{2}I}{ \pi a} \end{align} \)
円形コイルの作る磁界 \(H_2\) 大きさを求める
図2の円形コイルの磁界 \(H_2\) は,ビオ・バザールの法則より以下のように考えることができます。
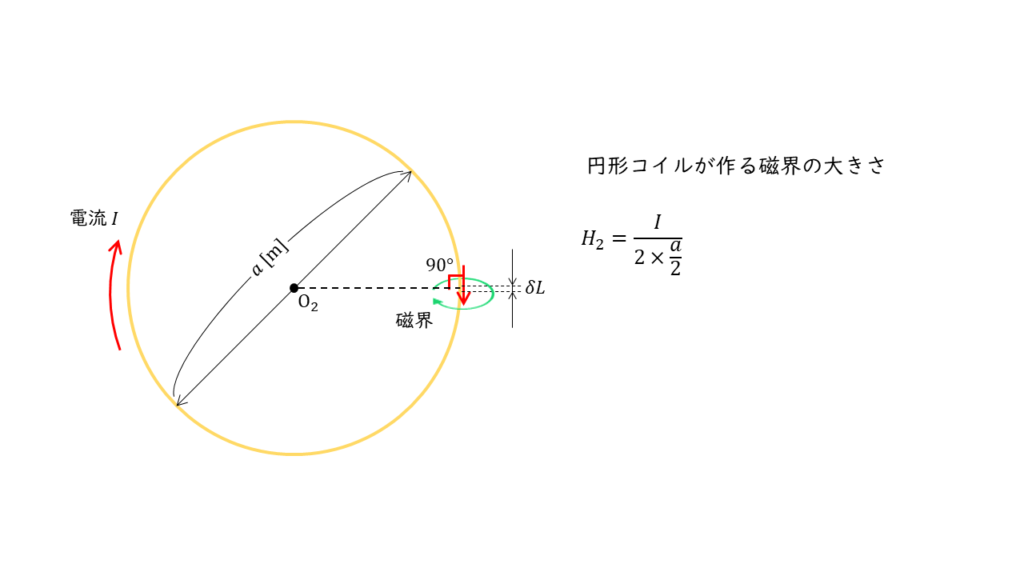
\( H_2 = \displaystyle \frac{I}{2 \times \displaystyle \frac{a}{2}} = \displaystyle \frac{I}{a} \)
磁界の大きさの比 \(\displaystyle \frac{H_1}{H_2}\) を求める
各コイルの磁界の大きさの比は,
\(\begin{align} \displaystyle \frac{H_1}{H_2} &= \displaystyle \frac{\displaystyle \frac{2\sqrt{2}I}{ \pi a}}{\displaystyle \frac{I}{a}} \\ \\ &= \displaystyle \frac{2\sqrt{2}}{\pi} \approx 0.9003 \end{align} \)
と計算することができ,答えは(2)となります。











コメント