問題
図のように,直流電源にスイッチ \(S\) ,抵抗 \(5\) 個を接続したブリッジ回路がある。この回路において,スイッチ \(S\) を開いたとき, \(S\) の両端間の電圧は \(1\ \rm V\) であった。スイッチ \(S\) を閉じたときに \(8\ \Omega\) の抵抗に流れる電流 \(I\) の値 \(\rm[A]\) として,最も近いものを次の(1)~(5)のうちから一つ選べ。
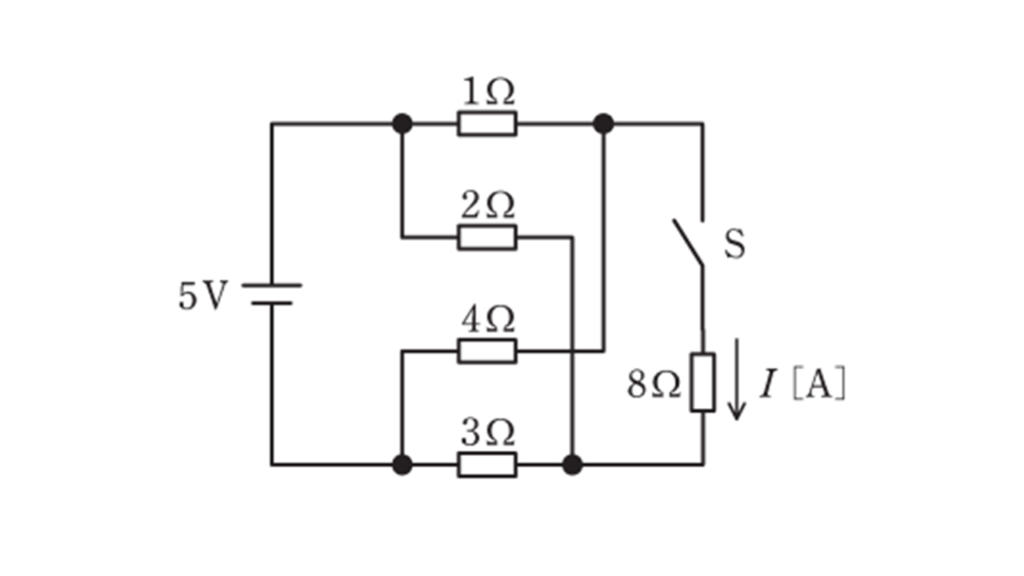
(1) \(0.10\) (2) \(0.75\) (3) \(1.0\) (4) \(1.4\) (5) \(2.0\)
解説
答え:(1)
回路図を書き換える
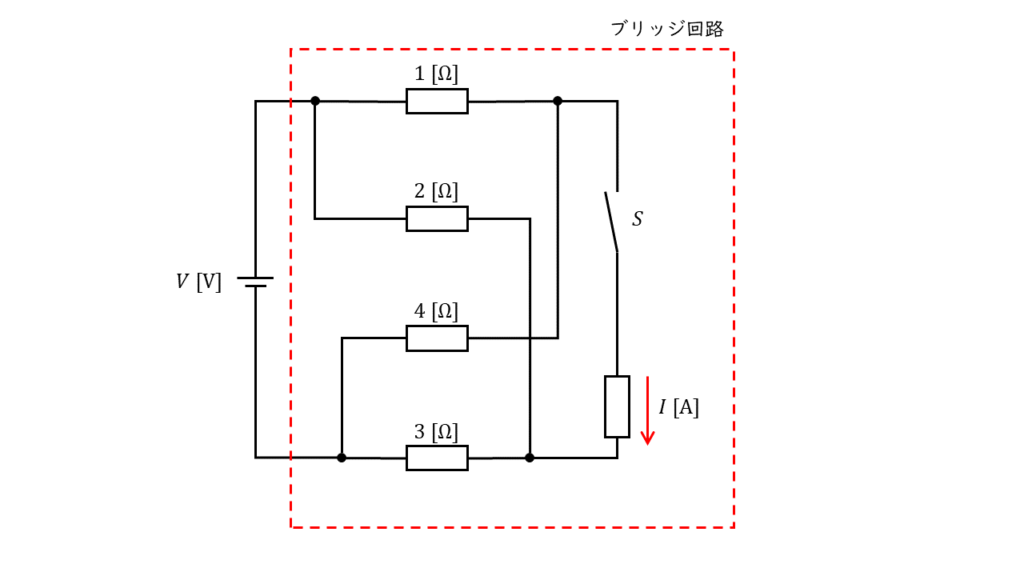
問題文より,回路図はブリッジ回路であることが分かりますが,問いの図のままでは回路をイメージしずらいため,下図のように書き換えます。
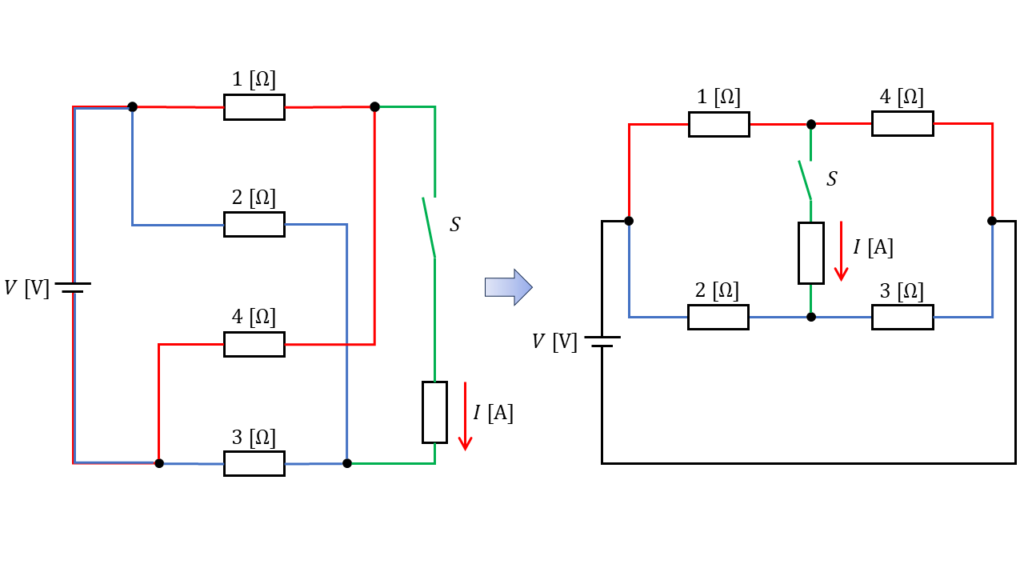
\(8\ \Omega\) の抵抗に流れる電流を求める
ブリッジ回路の橋渡し部分にある \(8\ \Omega\) の抵抗は,スイッチ \(S\) により初めは開放状態なので,下図のように考えることができます。
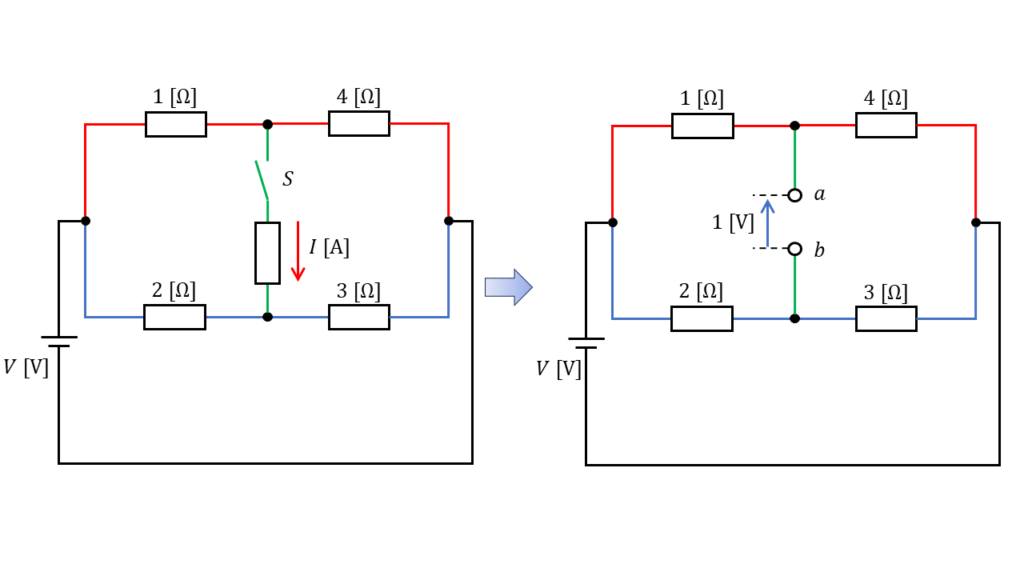
この形の回路は,『鳳・テブナンの定理』を用いて,内部抵抗を持つ電圧源と開放端に置き換えることができます。
問題文より,開放端部分の印加電圧は \(1\ \rm[V]\) とわかっているので,回路図から,内部抵抗の値を計算することで,\(8\ \Omega\) の抵抗に流れる電流を計算することできるようになります。
内部抵抗を計算する
『鳳・テブナンの定理』を使って電圧源の内部抵抗を考える場合,下図のように考えます。
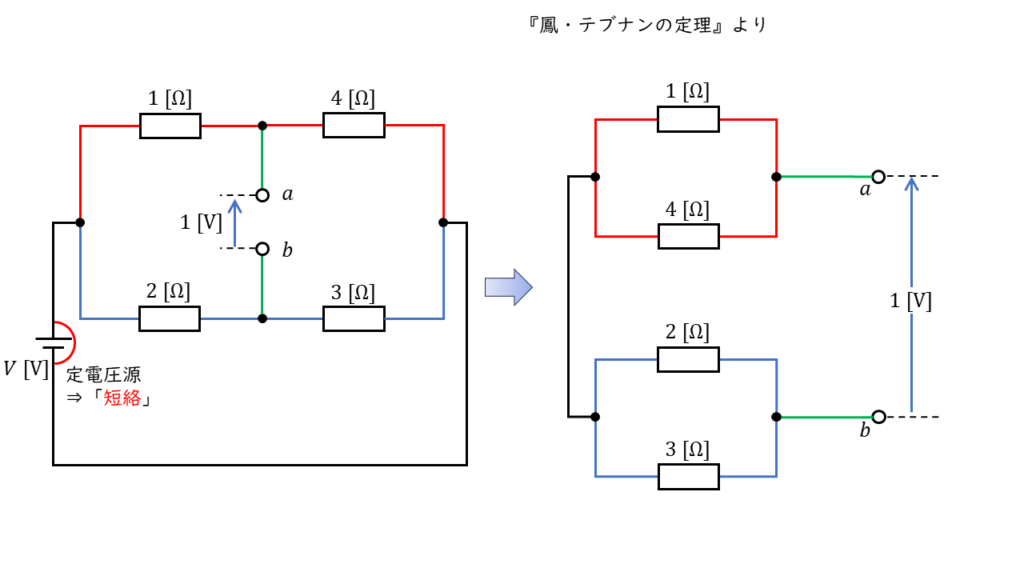
よって内部抵抗の大きさは,
\(\begin{align} R &= \displaystyle \frac{4 \times 1}{4+1} + \displaystyle \frac{2 \times 3}{2 + 3} \\ \\ &= \displaystyle \frac{4}{5} + \displaystyle \frac{6}{5} \\ \\ &= \displaystyle \frac{10}{5} \\ \\ &= 2 \ \Omega \end{align} \)
と計算できます。よって問の回路は,下図のように書き換えることができます。
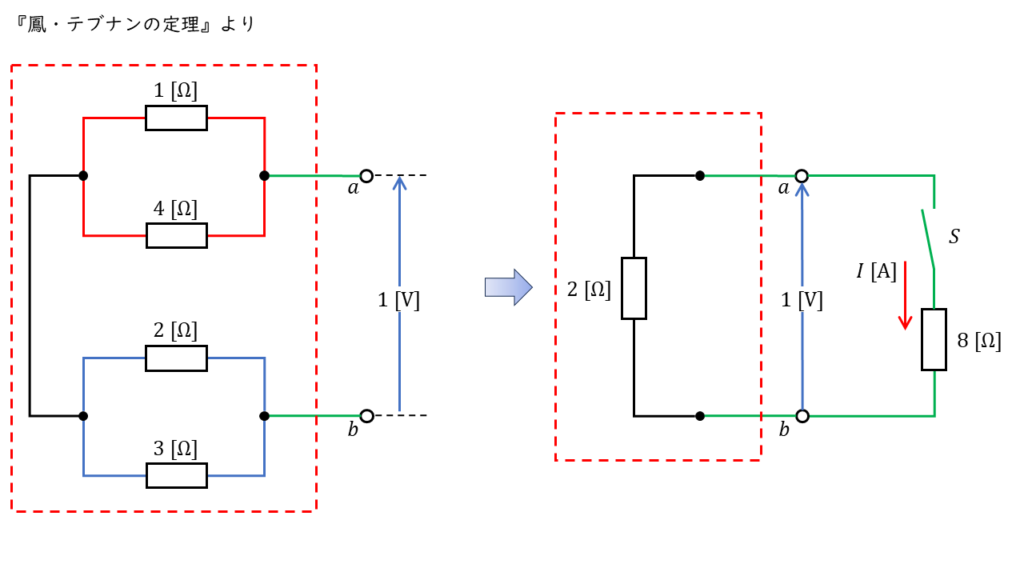
この時の回路を流れる電流の大きさは,
\(\begin{align} I &= \displaystyle \frac{1\ \rm V}{R + 8 \ \Omega} \\ \\ &= \displaystyle \frac{1}{2+8} \\ \\ &= \displaystyle \frac{1}{10} \\ \\ &= 0.1 \ \rm [A] \end{align} \)
となります。よって,答えは(1)となります。











コメント