【これだけ！】電験3種合格に必要な数学の範囲

電験3種に独学で挑戦しようと思ったときに初めにつまづくのが数学です。高校や大学でしっかりと数学を勉強してきた方にとっては当たり前の知識でも、卒業して数年が経過した方や文系の方にとっては非常に難しく感じます。

今回は独学で電験3種に合格したいと思ったときにどこまで数学が分かっていれば各科目の学習に進んでも支障が出ないかについて解説していきます。

電験3種合格に数学は必要か？

電験3種の合格には、計算問題を回答することが必須です。
一部を除き、中学校までに学習する数学の知識があれば、計算問題を解くことができます。

・分数の計算（小５）
・負の数を含む計算（中１）
・絶対値（中1）
・文字式と式の変形（中1）
・連立方程式（中2）
・図形の性質（中２）
・二次方程式（中3）
・三平方の定理（中3）
・ルート（√）の計算（中3）
・三角関数（中3～高1）
・ベクトル（中3理科、高2）
・円の公式（高２）
・複素数（高3）

難しそうに感じるベクトルや三角関数、複素数などは、交流回路の計算のために一部利用する程度なので、数学的に深く理解している必要はありません。
電験三種合格に必要なのは、計算方法を知っている程度の理解までで、十分に試験問題を解くことができます。

数学のオススメ参考書

計算が超苦手 or 分数からやり直しの人向け

計算が苦手で、分数からやり直したいという方は、手を動かして計算することに慣れる必要があります。
そのため、いきなり電験3種向けの数学参考書を購入してしまうと「レベルが高すぎてついていけない」と挫折してしまう原因になることもあります。

そこで、初歩の小・中学生向けの計算ドリルがおすすめです。
上で紹介している2冊は価格もお手頃で、勉強の習慣がない人にもプレッシャーを与えないページ数かつ、練習問題の数はしっかりしている問題集です。
冒頭に計算方法の記載もあるので、忙しくても2週間あれば終わらせられるボリュームになっています。

電験3種に特化した数学から勉強したい方へ

小・中学生向けの参考書では三角関数や複素数などは扱わないため、電験用に特化した数学の参考書は1冊は持っておくと公式などを忘れた際にすぐに調べられるので便利です。

数ある電験数学の参考書の中から電験3種に必要とされる知識が網羅されており、使いやすいと感じた3冊の参考書を紹介します。

	これだけ数学 改訂新版	電験3種かんたん数学 改訂3版	みんなが欲しかった! 電験三種合格へのはじめの一歩
学習範囲	行列など一部不要な部分がある	電顕3種の範囲のみ	電顕3種の範囲のみ
練習問題	普通	普通	少ない
電子書籍	kindle版 有り	kindle版 有り	kindle版 有り
ページ数	162[ページ]	172[ページ]	247[ページ]
デザイン	普通	1ページの情報量が多い	フルカラーで見やすい
価格	2,100円（税抜き）	2,000円（税抜き）	2,200円（税抜き）
	購入する	購入する	購入する

どの参考書も、「数学の解説→演習問題→電験の出題例→応用問題」の構成となっています。
電験の出題例については、科目の勉強を始める前は、ここで使うのくらいの気持ちで流し読みくらいでも問題ありません。

いきなり市販の参考書で学習するのが不安な方へ

電験教室は、市販の参考書よりもさらに内容をかみ砕き、電験三種に特化したオリジナル参考書を作成しました。

PDFのダウンロード版のみの販売となりますが、金額は1,000円としています。
また、販売記念として期間限定で、50%OFFにてSTORESで販売しています。

計算の基礎知識

ここからは、電験三種の計算に必要な基礎知識を簡単に紹介していきます。
参考書を購入する前の事前確認と思って読んでください。

分数の計算

分数の計算は意外に苦手に感じている方も多いです。つまづきやすい内容としては、通分、約分、分数の割り算、分数の分数があります。

通分

通分とは、分数の分母が違う場合に使用します。計算しやすくするために分母の数字を同じ数字でそろえる方法です。最も簡単な方法として、それぞれの分母の数字を掛け算します。

例題

\( \begin{align} \displaystyle \frac{1}{2} + \displaystyle \frac{1}{3} &= \displaystyle \frac{1 \times 3}{2 \times 3} + \displaystyle \frac{1 \times 2}{3 \times 2} \\ \\ &= \displaystyle \frac{3}{6} + \displaystyle \frac{2}{6} \\ \\ &= \displaystyle \frac{3+2}{6} = \displaystyle \frac{5}{6} \end{align} \)

この時の注意点は、分子にも同じ数字を掛け算することです。急いで計算しているときに忘れてしまいがちなので注意しましょう。

約分

約分とは、分母と分子が同じ数で割り算でる場合に使用します。分母の値を小さくできるので、後々の計算が楽になったり、数値を比較するときに役立ちます。

例題

\( \begin{align} \displaystyle \frac{16}{36} &= \displaystyle \frac{4 \times 4}{4 \times 9} \\ \\ &= \displaystyle \frac{4 \times 4 \div 4}{4 \times 9 \div 4} = \displaystyle \frac{4}{9} \end{align} \)

※分母と分子がともに偶数（最後の数字が0，2，4，6，8）で終わる数字の場合は必ず2で約分できます。

分数の割り算

電験3種の計算問題を解き進めている中で、分数を割り算する場面が出てきます。分数の割り算では\(\div\)の記号の後ろにある数字の分子と分母をひっくり返した数字の掛け算にすることで計算ができます。また、分子と分母をひっくり返した数字のことを逆数と呼びます。

例題1

\( \begin{align} \displaystyle \frac{2}{5} \div \displaystyle \frac{4}{3} &= \displaystyle \frac{2}{5} \times \displaystyle \frac{3}{4} \\ \\ &= \displaystyle \frac{2 \times 3}{5 \times 4} \\ \\ &= \displaystyle \frac{6}{20} = \displaystyle \frac{3}{10} \end{align} \)

例題2

\( \begin{align} \displaystyle \frac{2}{3} \div 2 &= \displaystyle \frac{2}{3} \times \displaystyle \frac{1}{2} \\ \\ &= \displaystyle \frac{2 \times 1}{3 \times 2} \\ \\ &= \displaystyle \frac{2}{6} = \displaystyle \frac{1}{3} \end{align} \)

分数の分数

交流回路のインピーダンスを計算する場面などで使用します。計算の仕方はそれほど難しいというわけではないのですが、初見では戸惑うことも多いので身に着けておきましょう。

例題

\( \begin{align} \displaystyle \frac{1}{1 + \frac{2}{3}} &= \displaystyle \frac{1}{\frac{2}{2} + \frac{2}{3}} \\ \\ &= \displaystyle \frac{1}{\frac{4}{3}} \\ \\ &= \displaystyle \frac{1 \times 3}{\displaystyle \frac{4}{3} \times 3} = \displaystyle \frac{3}{4} \end{align} \)

式変形

電験3種では公式を変形して問題を解くことが多いです。また、途中計算を効率よく進めるためにも必要な計算力になります。式変形ができるようになるだけで公式を暗記する量が少なくなり勉強も楽になるはずです。しっかり身に着けておきましょう。

例題 電圧\(10\ [V]\)，抵抗\(5\ [Ω]\)の回路を流れる電流の大きさをオームの法則\(V = R \times I\)を用いて計算する。

\( \begin{align} V &= R\times I \\ V \times \frac{1}{R} &= R \times I \times \frac{1}{R} \\ \frac{V}{R} &= I \\ I &=\frac{V}{R} \\ I &= \frac{10}{5} = 2\ [A] \end{align} \)

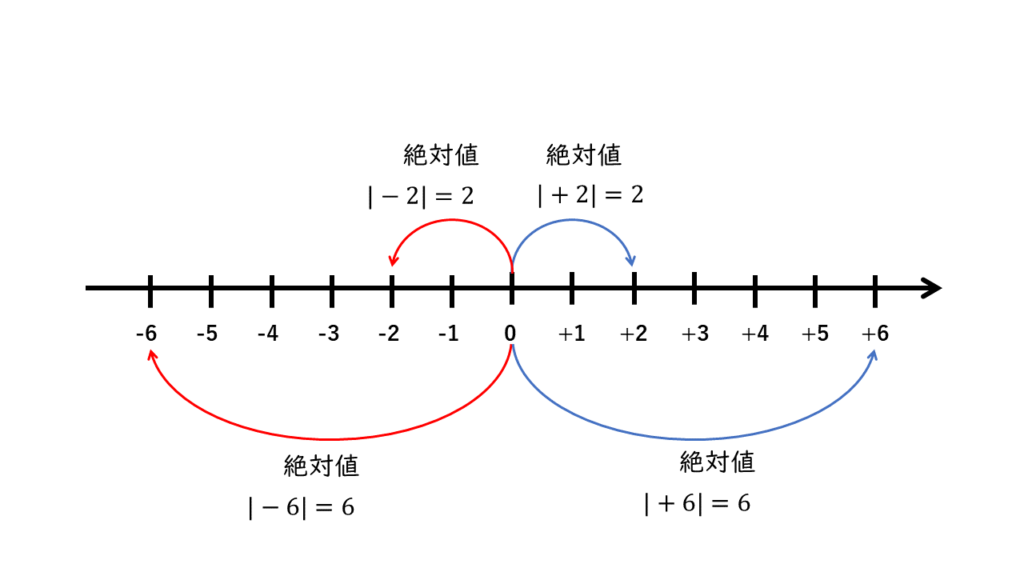
絶対値

絶対値は電位差を求める問題や交流回路のインピーダンス計算などで使用することがあります。ゼロからどのくらい離れているかを表すもので、プラスやマイナスを考えない値のことです。

三角関数

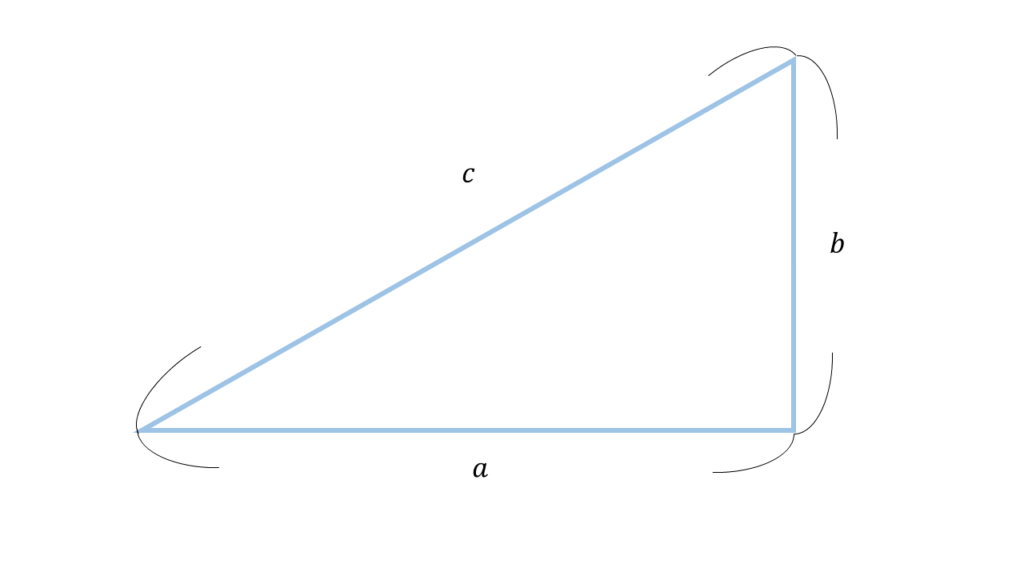
交流回路を流れる電流やインピーダンスの計算に必要な知識です。また、モーター（電動機）のトルクや電線の風圧荷重計算の場面でも役立ちます。

ルート（√）の計算

交流回路の計算などでルート（√）はよく登場します。計算の進め方だけ覚えておけば大丈夫です。√の値については電卓が使用できるので暗記する必要はありません。

計算方法をしっかりマスターしましょう。

例題1

\(\sqrt{2} + \sqrt{3} \approx 1.414 + 1.732 = 3.146 \)

例題2

\( \begin{align} \sqrt{2} + \sqrt{8} &=\sqrt{2} + 2\sqrt{2} \\ \\ &= 3\sqrt{2} \\ &\approx 3 \times 1.414 = 4.242 \end{align} \)

√の中の数字が異なる場合そのまま足し算することはできないので注意しましょう。

円の公式

円の公式については必須事項ではありませんが、円の公式と面積の式は覚えておいた方がいいです。点電荷の電気力線の密度や電流の作る磁界を理解するときの助けになります。また今後、電験2種に挑戦しようと思ったとき必要になります。

\( \begin{align} \bf{円の公式}　&x^2 + y^2 = r^2 \\ \\ \bf{円の面積}　&S = \pi r^2 \\ \\ \bf{円周の長さ}　&l = 2\pi r \end{align} \)

複素数

複素数は電力の計算や交流回路の計算に必要な計算知識です。聞きなれない方も多いかもしれませんが、それほど難しくはありません。覚えることは次の3つです。

• 複素記号には、\( J \)を使用し、\( J^2 = -1\)になる。
• 複素数同士でしか、足し引き出来ない。
• 複素数を含む場合の絶対値は以下の様に計算する。
  \(\begin{align} | 2 + j2\sqrt{3} | &= \sqrt{2^2 + (2\sqrt{3})^2} \\ \\ &= \sqrt{4 + (2^2 \times (\sqrt{3})^2 } \\ \\ &= \sqrt{4 + 4 \times 3} \\ \\ &= \sqrt{16} = 4 \end{align} \)

まとめ

電験3種に独学で挑戦するには初めに数学の知識は必須です。学習範囲はそれほど広くはありませんが、学校を卒業してからはあまり使用しない内容もあるので、現役の学生以外は参考書で一度確認しておくことをおすすめします。

・分数の計算（小５）
・負の数を含む計算（中１）
・絶対値（中1）
・文字式と式の変形（中1）
・連立方程式（中2）
・図形の性質（中２）
・二次方程式（中3）
・三平方の定理（中3）
・ルート（√）の計算（中3）
・三角関数（中3～高1）
・ベクトル（中3理科、高2）
・円の公式（高２）
・複素数（高3）

電験3種の数学について質問したいこと，わからないこと等ございましたら、お問い合わせからお気軽にご連絡ください。