問題
次の文章は,コイルの磁束鎖交数とコイルに蓄えられる磁気エネルギーについて述べたものである。
インダクタンス \(1\ \rm[mH]\) のコイルに直流電流 \(10\ \rm[A]\) が流れているとき,このコイルの磁束鎖交数 \(\psi_1 \ \rm[Wb]\) は \( \fbox{ (ア) } \) \(\rm [Wb]\) である。また,コイルに蓄えられている磁気エネルギー \(W_1\ \rm[J]\) は \( \fbox{ (イ) } \) \(\rm[J]\) である。
次に,このコイルに流れる直流電流を \(30\ \rm[A]\) とすると,磁束鎖交数 \(\psi_2\ \rm[Wb]\) と蓄えられる磁気エネルギー \(W_2\ \rm[J]\) はそれぞれ \( \fbox{ (ウ) } \) となる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句又は数値として,正しいものを組み合わせたのは次のうちどれか。
$$ \begin{array}{cccc} \ &(ア)&(イ)&(ウ)\\ \hline (1) &5 \times 10^{-3} &5 \times 10^{-2} &\psi_2 は \psi_1 の3倍,W_2 は W_1 の9倍 \\ \hline (2) &1 \times 10^{-2} &5 \times 10^{-2} &\psi_2 は \psi_1 の3倍,W_2 は W_1 の9倍 \\ \hline (3) &1 \times 10^{-2} &1 \times 10^{-2} &\psi_2 は \psi_1 の9倍,W_2 は W_1 の3倍 \\ \hline (4) &1 \times 10^{-2} &5 \times 10^{-1} &\psi_2 は \psi_1 の3倍,W_2 は W_1 の9倍 \\ \hline (5) &5 \times 10^{-2} &5 \times 10^{-1} &\psi_2 は \psi_1 の9倍,W_2 は W_1 の27倍 \\ \hline \end{array} $$
解説
答え:(2)
コイルに生じる磁束の大きさ
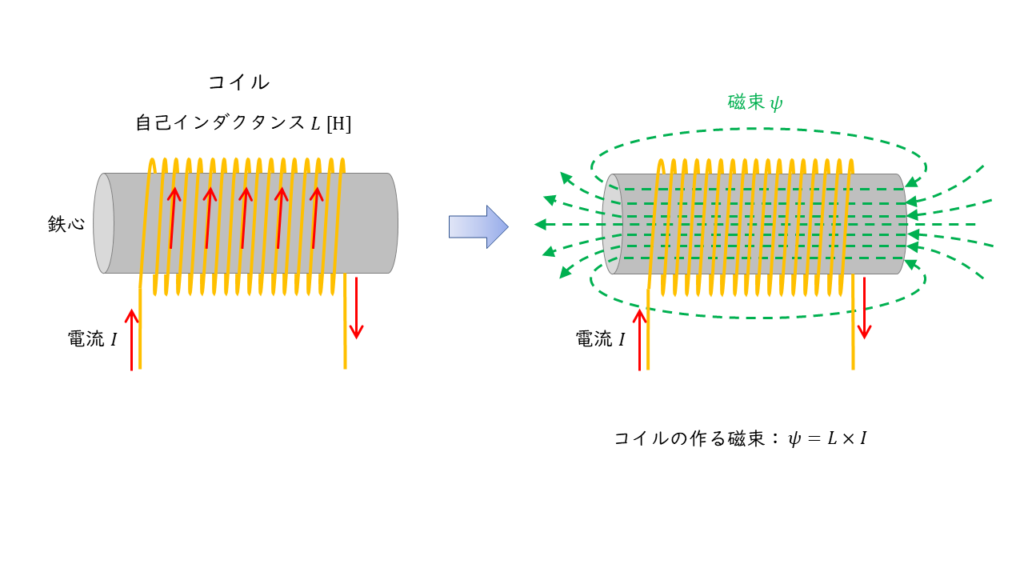
自己インダクタンス \(L\ \rm[H]\) のコイルに電流を \(I\ \rm[A]\) 流すときに生じる磁束 \(\psi\ \rm[Wb]\) は,
\( \psi = L \times I \)
で表されます。したがって,コイルに\(10\ \rm A\)の電流を流した時に生じる磁束 \(\psi_1\) とコイルに \(30\ \rm A\)の電流を流した時に生じる磁束 \(\psi_2\) の大きさは,それぞれ以下のように計算できます。
\( \psi_1 = 1.0 \times 10^{-3} \times 10 = 1.0 \times 10^{-2} \)
\( \psi_2 = 1.0 \times 10^{-3} \times 30 = 3.0 \times 10^{-2} \)
この結果から,磁束 \(\psi_2\) は,磁束 \(\psi_1\) の \(3倍\) になっているといえます。
コイルに蓄えられる磁気エネルギーの大きさ
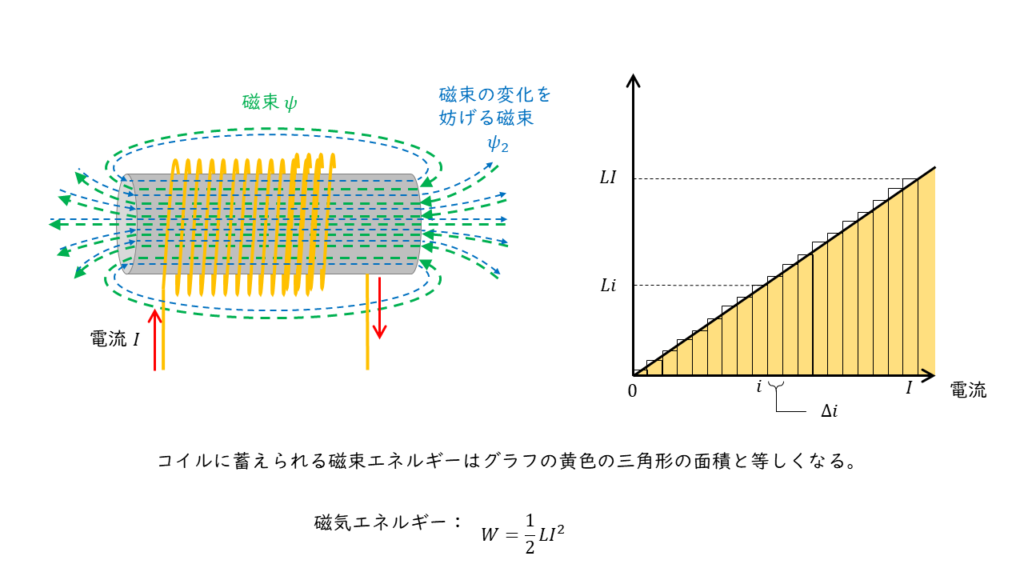
自己インダクタンス \(L\ \rm[H]\) のコイルに電流を \(I\ \rm[A]\) 流すときにコイルに蓄えられる磁気エネルギー \(W\ \rm[J]\) は,
\( W = \displaystyle \frac{1}{2}LI^2 \)
で表されます。したがって,コイルに\(10\ \rm A\)の電流を流した時に蓄えられる磁気エネルギー \(W_1\) とコイルに \(30\ \rm A\)の電流を流した時に蓄えられる磁気エネルギー \(W_2\) の大きさは,それぞれ以下のように計算できます。
\( W_1 = \displaystyle \frac{1}{2} \times 1.0 \times 10^{-3} \times 10^{2} = 5.0 \times 10^{-2} \)
\(\begin{align} W_2 &= \displaystyle \frac{1}{2} \times 1.0 \times 10^{-3} \times 30^{2} \\ &=9 \times 5.0 \times 10^{-2} \\ &= 4.5 \times 10^{-1} \end{align} \)
この結果から,磁気エネルギー \(W_2\) は,磁束 \(W_1\) の \(9倍\) になっているといえます。
以上のことから,答えは(2)になります。











コメント