問題
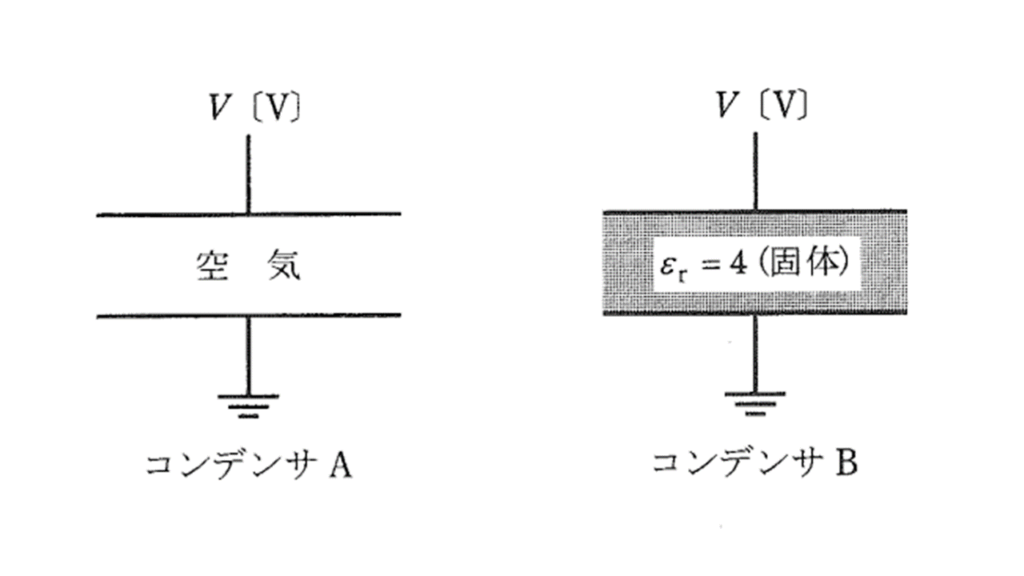
図に示すように,電極板面積と電極板間隔がそれぞれ同一の 2 種類の平行平板コンデンサがあり,一方を空気コンデンサ A ,他方を固体誘電体(比誘電率 \(\varepsilon_r = 4\) )が満たされたコンデンサ B とする。両コンデンサにおいて,それぞれ一方の電極に直流電圧 \(V\) [V] を加え,他方の電極を接地したとき,コンデンサ B の内部電界 [V/m] 及び電極板上に蓄えられた電荷 [C] はコンデンサ A のそれぞれ何倍となるか。その倍率として,正しいものを組み合わせたのは次のうちどれか
ただし,空気の比誘電率を \(1\) とし,コンデンサの端効果は無視できるものとする。
$$ \begin{array}{ccccc} \ & 内部電界 & 電荷 \\ \hline (1) &1 &4 \\ \hline (2) &4 &4 \\ \hline (3) &\displaystyle \frac{1}{4} &4 \\ \hline (4) &4 &1 \\ \hline (5) &1 &1 \\ \hline \end{array} $$
解説
答え:(1)
コンデンサA,Bの静電容量を求める
問題文より,「電極板面積と電極板間隔がそれぞれ同一 … 」と記載があるので,
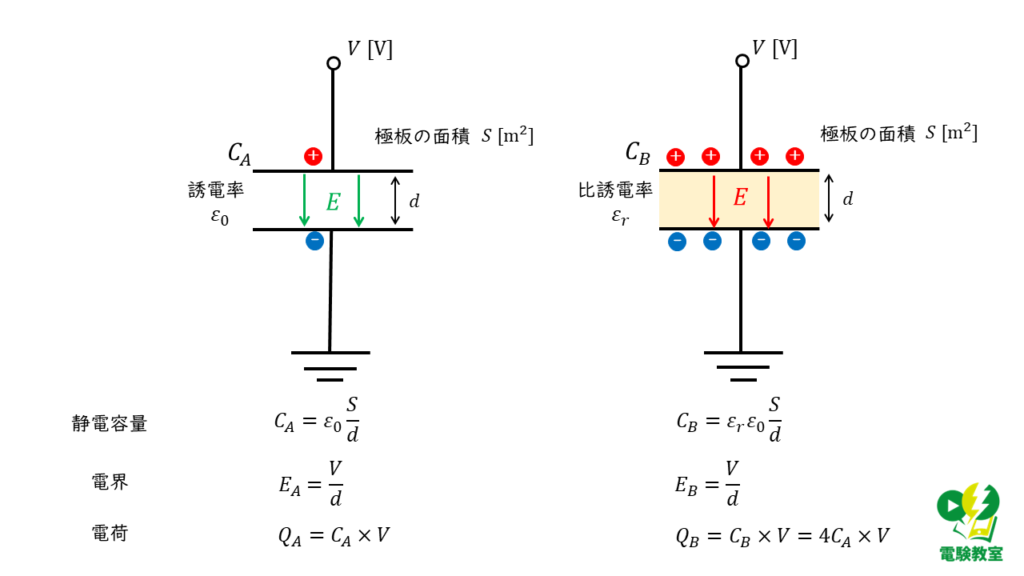
極板間距離 \(d\ \rm [m]\) ,極板の面積 \( S\ \rm [m^2] \) ,空気中の誘電率 \(\varepsilon_0 \ \rm [F/m] \) で表すとした場合,コンデンサA,Bそれぞれの静電容量\( C_A \ \rm [F]\) , \(C_B \ \rm [F]\) は,
\( C_A = \varepsilon \displaystyle \frac{S}{d} \)
\( C_B = \varepsilon_r \varepsilon_0 \displaystyle \frac{S}{d} = 4 \varepsilon_0 \displaystyle \frac{S}{d} = 4C_A\)
コンデンサA,Bの内部電界を求める
平行平板コンデンサの内部電界 \(E \ \rm [V/m] \)は,コンデンサに印加する電圧の大きさを \(V \ \rm [V] \),極板間距離を \(d \ \rm [m] \)とすると ,
\( E = \displaystyle \frac{V}{d} \)
で表すことができます。
問題文より電圧は\(V \ \rm [V]\)で同じ大きさとなるので,コンデンサA,Bの内部電界\( E_A\) ,\(E_B\)はそれぞれ,
\( E_A = \displaystyle \frac{V}{d} \)
\( E_B = \displaystyle \frac{V}{d} = E_A \)
となるため,\(E_B\)は,\(E_A\)の1倍となります。
コンデンサA,Bに蓄えられる電荷の量を求める
平行平板コンデンサに蓄えられる電荷量 \(Q \ \rm [C] \) は,コンデンサの両端に印加される電圧を \(V \ \rm [V] \),静電容量を \( C \ \rm [F] \)とすると,
\( Q = C \times V \)
で表すことができます。したがって,コンデンサA,Bに蓄えられる電荷量 \(Q_A \) ,\(Q_B\)は,
\( Q_A = C_A \times V \)
\( Q_B = C_B \times V = 4C_A \times V \)
となり,\(Q_B\)は,\(Q_A\)の4倍であることが分かります。
よって答えは,(1)となります。











コメント