問題
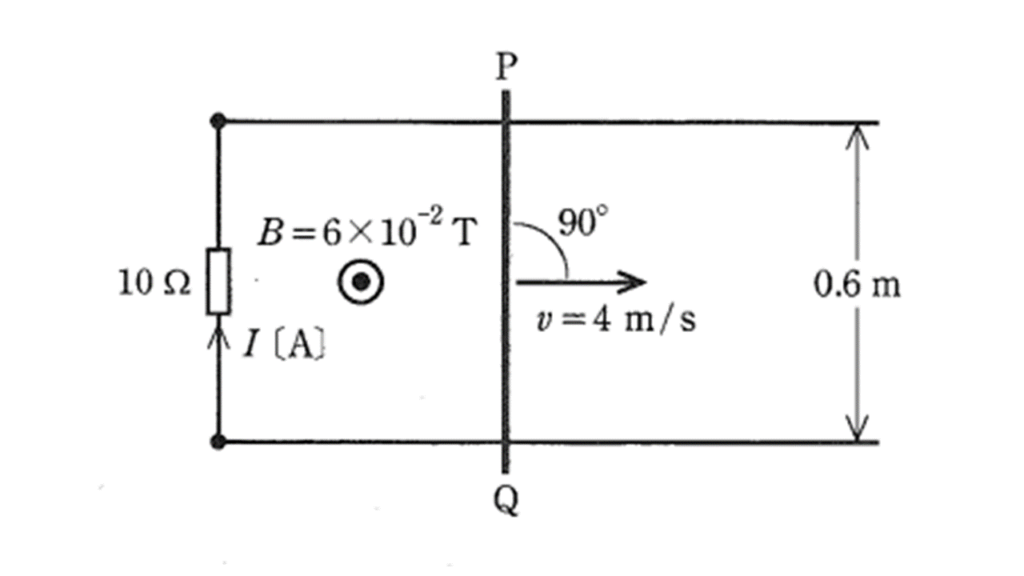
紙面に平行な水平面内において, \(0.6\ \rm[m]\) の間隔で張られた \(2\) 本の直線状の平行導線に \(10\ \rm[\Omega]\) の抵抗が接続されている。この平行導線に垂直に,図に示すように,直線状の導体棒 \(\rm PQ\) を渡し,紙面の裏側から表側に向かって磁束密度 \(B = 6 \times 10^{-2}\ \rm[T]\) の一様な磁界をかける。 ここで,導体棒 \(\rm PQ\) を磁界と導体棒に共に垂直な矢印の方向に一定の速さ \(v = 4\ \rm[m/s]\) で平行導線上を移動させているときに, \(10\ \rm[\Omega]\) の抵抗に流れる電流 \(I\ \rm[A]\) の値として,正しいのは次のうちどれか。
ただし,電流の向きは図に示す矢印の向きを正とする。 また,導線及び導体棒 \(\rm PQ\) の抵抗,並びに導線と導体棒との接触抵抗は無視できるものとする。
(1) \(−0.0278\) (2) \(−0.0134\) (3) \(−0.0072\) (4) \(0.0144\) (5) \(0.0288\)
解説
答え:(4)
誘導起電力の大きさと向きを求める
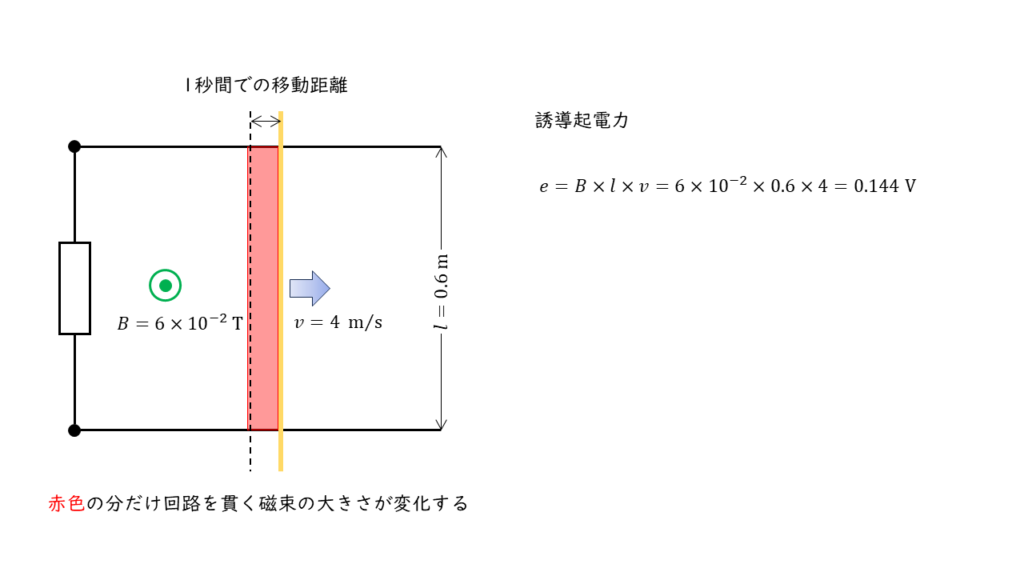
問の図より,磁界中を移動する導体棒 \(\rm PQ\) の長さは \(0.6\ \rm m\) ,導体棒の移動速度は \(v = 4\ \rm m/s\) ,磁界の大きさ \( B = 6 \times 10^{-2}\ \rm T\) であるから誘導起電力 \(e\ \rm V\) の大きさは,
\(\begin{align} e &= Blv \\ &= 6 \times 10^{-2} \times 0.6 \times 4 \\ &= 0.144 \ \rm V \end{align} \)
と計算することができます。誘導起電力の向きは『フレミングの右手の法則』より,下図のようになります。
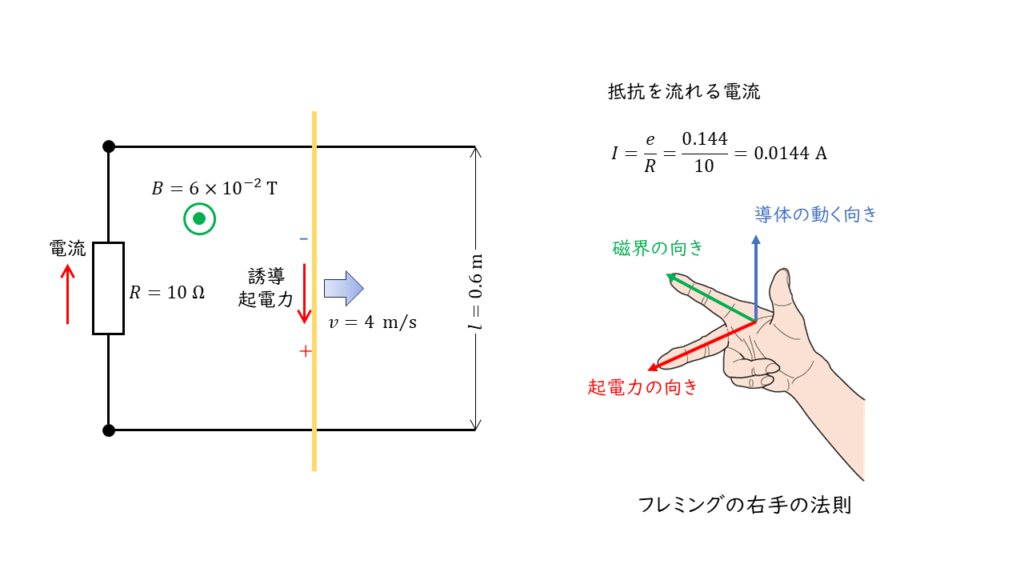
抵抗を流れる電流 \( I \) の大きさを求める
オームの法則より,\(10 \ \Omega\) の抵抗を流れる電流 \(I\) は,
\(\begin{align} I &= \displaystyle \frac{e}{R} \\ \\ &= \displaystyle \frac{0.144}{10} = 0.0144 \end{align} \)
と計算できます。したがって、答えは(4)となります。











コメント