【過去問解説】H23年理論　問2　コンデンサに関する計算問題

問題

直流電圧 \(1000\) [V] の電源で充電された静電容量 \(8\) [μF] の平行平板コンデンサがある。コンデンサを電源から外した後に電荷を保持したままコンデンサの電極間距離を最初の距離の \(\displaystyle \frac{1}{2}\) に縮めたとき，静電容量 [μF] と静電エネルギー [J] の値の組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

$$ \begin{array}{ccc} \ &　静電容量　 &　静電エネルギー　 \\ \hline (1) & 16 &4 \\ \hline (2) &16 & 2 \\ \hline (3) &16 &8 \\ \hline (4) &4 &4 \\ \hline (5) &4 &2 \\ \hline \end{array} $$

解説

答え：(2)

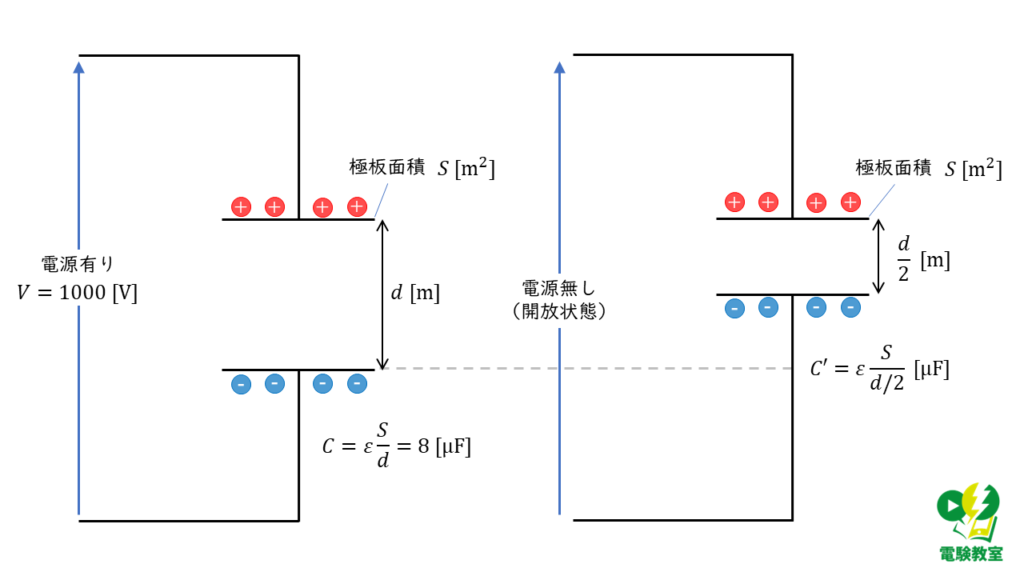
静電容量を求める

平行平板コンデンサの静電容量 \( C \) [F]は，極板の面積を \(S\) [\( \rm m^2\)]，極板間距離を \(d\) [\(\rm m\)]，誘電率を \(\varepsilon\) [\(\rm F/m \)]とすると，

\( C = \varepsilon \displaystyle \frac{S}{d} \)

で表すことができます。

静電容量が，\(8\) [μF]の平行平板コンデンサの極板間距離を\( \displaystyle \frac{1}{2} \)にすると，静電容量\( C’ \)は，

\( \begin{align} C’ &= \varepsilon \displaystyle \frac{S}{\displaystyle \frac{d}{2}} \\ \\ &= \varepsilon \displaystyle \frac{2S}{d} \\ \\ &= 2\times C \\ \\ C’ &= 2 \times 8 = 16 \end{align} \)

となります。

静電エネルギーを求める

初めにコンデンサに蓄えられた電荷量 \(Q\) [C]は，

\( \begin{align} Q &=C \times V \\ \\ &= 8\times 10^{-6} \times 1000 \\ \\ &= 8 \times 10^{-3} \ [\rm C] \end{align} \)

と計算できます。

電源から切り離したコンデンサを電荷を保ったまま，極板間距離を\(\displaystyle \frac{1}{2}\)としているので，静電エネルギー \(W\) [J]を求める式は，

\( W = \displaystyle \frac{Q^2}{2C}\)

を用いて計算することができます。この時、コンデンサは電源から切り離されているため、蓄えられている電荷の\(Q\) [C]の大きさは変化しません。

電荷\( Q = 8 \times 10^{-3}\) [C]と極板間を縮めた後の静電容量 \( C’ = 16\) [μF]を式に代入し計算すると，

\( \begin{align} W &= \displaystyle \frac{\left( 8 \times 10^{-3} \right)^2 }{2 \times16 \times 10^{-6} } \\ \\ &= \displaystyle \frac{8 \times 8 \times 10^{-6} }{ 2 \times 16 \times 10^{-6} } = 2 \ [ \rm J] \end{align} \)

よって答えは，(2)になります。