問題
次の文章は,磁界中に置かれた導体に働く電磁力に関する記述である。
電流が流れている長さ \(L\ \rm[m]\) の直線導体を磁束密度が一様な磁界中に置くと,フレミングの \( \fbox{ (ア) } \) の法則に従い,導体には電流の向きにも磁界の向きにも直角な電磁力が働く。直線導体の方向を変化させて,電流の方向が磁界の方向と同じになれば,導体に働く力の大きさは \( \fbox{ (イ) } \) となり,直角になれば, \( \fbox{ (ウ) } \) となる。力の大きさは,電流の \( \fbox{ (エ) } \) に比例する。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{llll} \ &(ア)&(イ)&(ウ)&(エ)\\ \hline (1) &左 手 &最 大 &零 &2 乗 \\ \hline (2) &左 手 &零 &最 大 &2 乗 \\ \hline (3) &右 手 &零 &最 大 &1 乗 \\ \hline (4) &右 手 &最 大 &零 &2 乗 \\ \hline (5) &左 手 &零 &最 大 &1 乗 \\ \hline \end{array} $$
解説
答え:(5)
磁界中を流れる電流にはたらく力
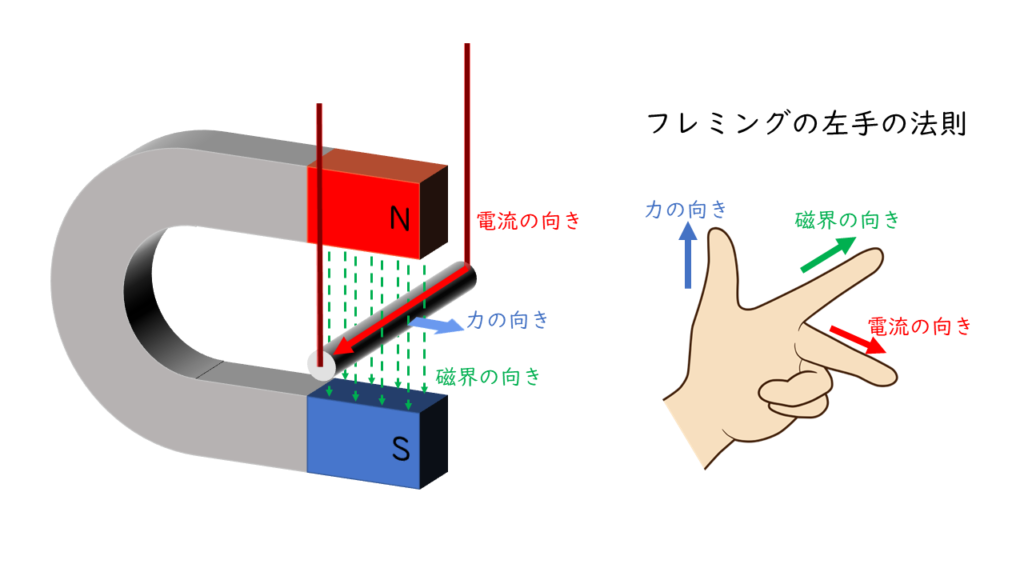
上図のように磁界の中に置かれた導体に電流が流れると,電磁力が働きます。磁界,電流,電磁力のベクトル(方向)は『フレミングの左手の法則』に従います。
電磁力と導体-磁界の作る角度の関係
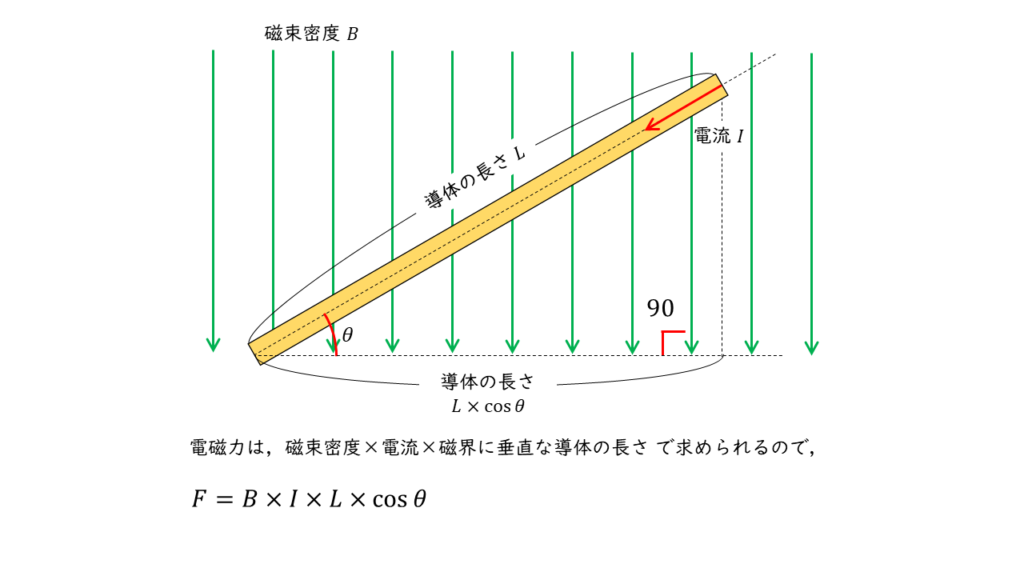
フレミングの左手の法則より,磁界 \(B\ \rm [T]\)に対して直角に交わる電流 \(I \ \rm [A]\) に電磁力 \(F\ \rm [N]\) が発生します。磁界中にある導体の長さを \(L\ \rm [m]\) とした場合,関係式は,
\( F = B \times I \times L \times \cos\theta \)
となり、磁束密度と電流の大きさに比例します。
\( \cos\theta\) は,90°(直角)の時に最大となり,0°の時に最小となるので,電磁力は以下のようになります。
電流の方向が磁界の方向と同じになる:電磁力は『零』となる
電流の方向が磁界の方向と直角になる:電磁力は『最大』となる
以上のことから,答えは(5)となります。











コメント