問題
次の文章は,コイルのインダクタンスに関する記述である。ここで,鉄心の磁気飽和は,無視できるものとする。
均質で当断面の環状鉄心に被覆電線を巻いてコイルを作成した。このコイルの自己インダクタンスは,巻数の \( \fbox{ (ア) } \) に比例し,磁路の \( \fbox{ (イ) } \) に反比例する。
同じ鉄心にさらに被覆電線を巻いて別のコイルを作ると,これら二つのコイルの間には相互インダクタンスが生じる。相互インダクタンスの大きさは,漏れ磁束が \( \fbox{ (ウ) } \) なるほど小さくなる。それぞれのコイルの自己インダクタンスを \(L_1\ \rm[H]\) ,\(L_2\ \rm[H]\) とすると,相互インダクタンスの最大値は \( \fbox{ (エ) } \) \(\rm[H]\) である。
これら二つのコイルを \( \fbox{ (オ) } \) とすると,合成インダクタンスの値は,それぞれの自己インダクタンスの合計よりも大きくなる。
上記の記述中の空欄箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組み合わせとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{cccccc} \ &(ア)&(イ)&(ウ)&(エ)&(オ)\\ \hline (1) &1乗 &断面積 &少なく &L_1 + L_2 &差動接続 \\ \hline (2) &2乗 &長 さ &多 く &L_1 + L_2 &和動接続 \\ \hline (3) &1乗 &長 さ &多 く &\sqrt{L_1 L_2} &和動接続 \\ \hline (4) &2乗 &断面積 &少なく &L_1 + L_2 &差動接続 \\ \hline (5) &2乗 &長 さ &多 く &\sqrt{L_1 L_2 } &和動接続 \\ \hline \end{array} $$
解説
答え:(5)
コイルの自己インダクタンス
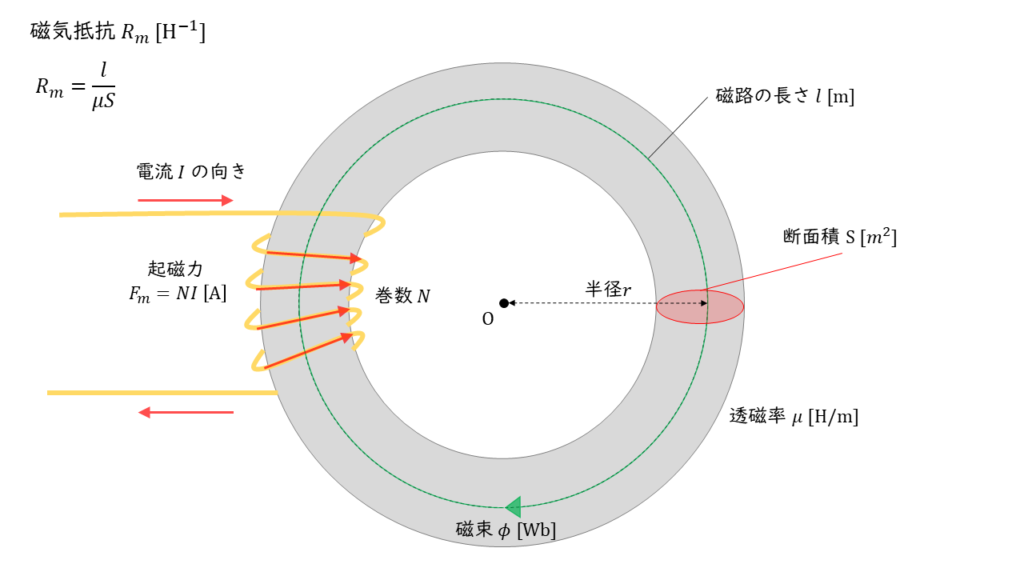
上図のようなコイルの場合,自己インダクタンスを \(L_1 \ \rm H\),コイルを流れる電流を \(I\ \rm A\) ,巻数を \(N\) ,鎖交磁束を \(\phi\) とすると,以下の関係式が成り立ちます。
\(\begin{align} L_1 I &= N \phi \\ L_1 &= \displaystyle \frac{N\phi}{I} \tag{1} \end{align} \)
鎖交磁束 \(phi\) は,磁束密度を \(B\ \rm T\) ,鉄心の断面積を \(S\ \rm m^2\) ,透磁率を \( \mu \ \rm H/m\) ,磁界の大きさを \(H\ \rm A/m\),磁路の長さを \(l\ \rm m\) とすると,
\(\begin{align} \phi &= B \times S \\ &= \mu H \times S \\ &= \mu \displaystyle \frac{NI}{l} \times S \\ &= \displaystyle \frac{\mu N I S}{l} \tag{2} \end{align} \)
式(1),(2)より自己インダクタンス\(L_1\)は,
$$ \begin{align} L_1 &= \displaystyle \frac{N}{I} \phi \\ \\ &=\displaystyle \frac{N}{I} \times \displaystyle \frac{\mu NIS}{l} \\ \\ L_1 &= \displaystyle \frac{\mu S N^2}{l} \end{align} $$
と書き表すことができるため,自己インダクタンスは,「巻数の2乗」に比例し,「磁路の長さ」に反比例します。
コイルの相互インダクタンス
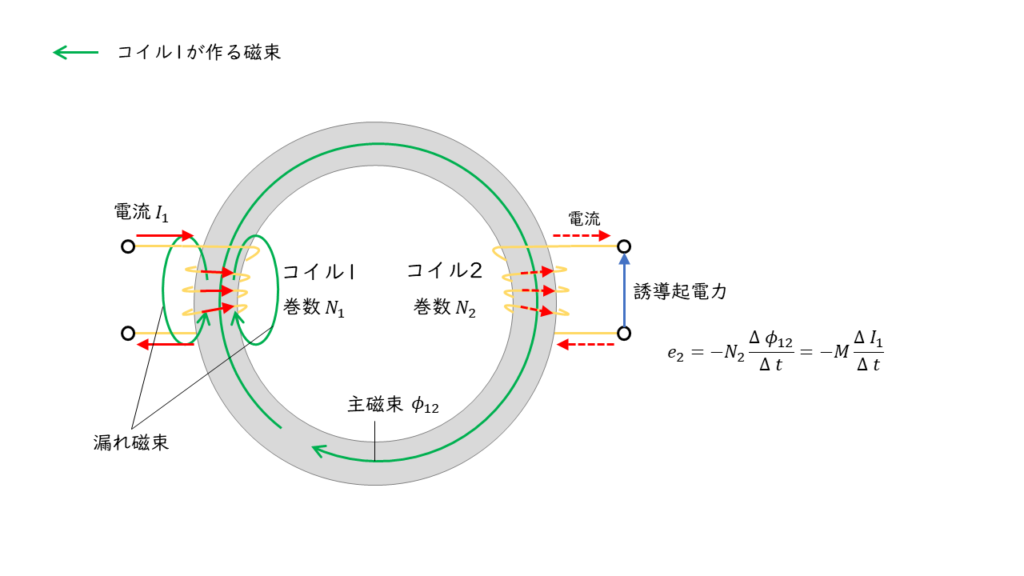
上図より,コイル1に電流が流れると磁束が発生し,コイル1だけ貫く磁束とコイル1とコイル2の両方を貫く磁束に分かれます。この時,2つのコイルを貫く磁束は,コイル2にも誘導起電力 \(e_2\) を発生させます。この現象を相互誘導といい,相互誘導の影響度合いを表したものが相互インダクタンスです。
相互インダクタンス \(M\) は,コイル1の自己インダクタンス \(L_1\) とコイル2の自己インダクタンス \(L_2\) を用いて,
\( M = \sqrt{L_1 L_2} \)
と表すことができます。
したがって,コイル1の漏れ磁束が多くなると2つのコイルを貫く磁束が少なくなるため,コイル2に発生する起電力 \(e_2\) は小さくなります。すなわち,相互インダクタンスが小さくなったと考えられます。
コイルの接続
コイルの接続方法には,「和動接続」と「差動接続」の2つがあります。
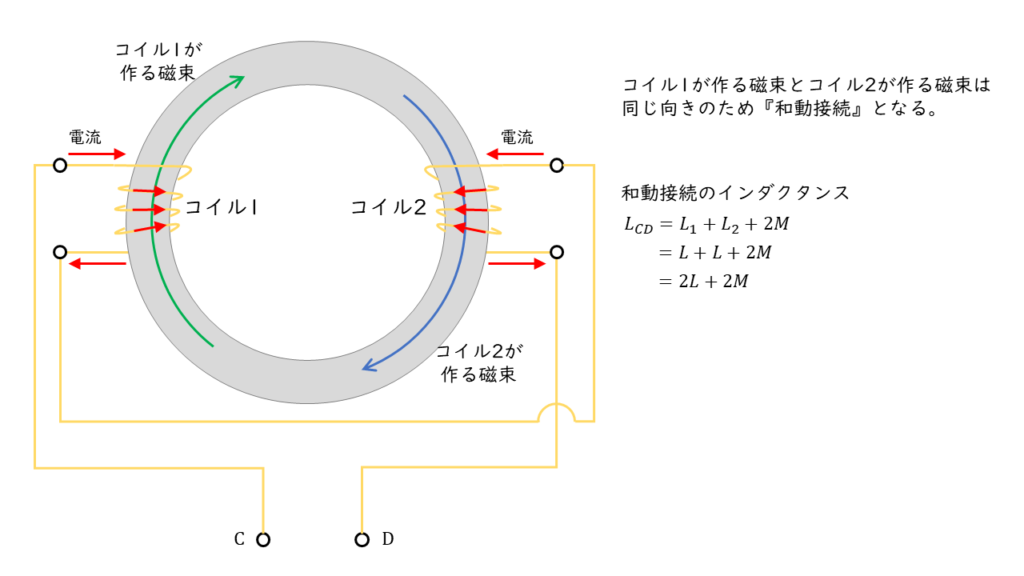
和動接続…下図のように各コイルの作る磁界が同じ向きになり,磁束を強めあう接続方法です。
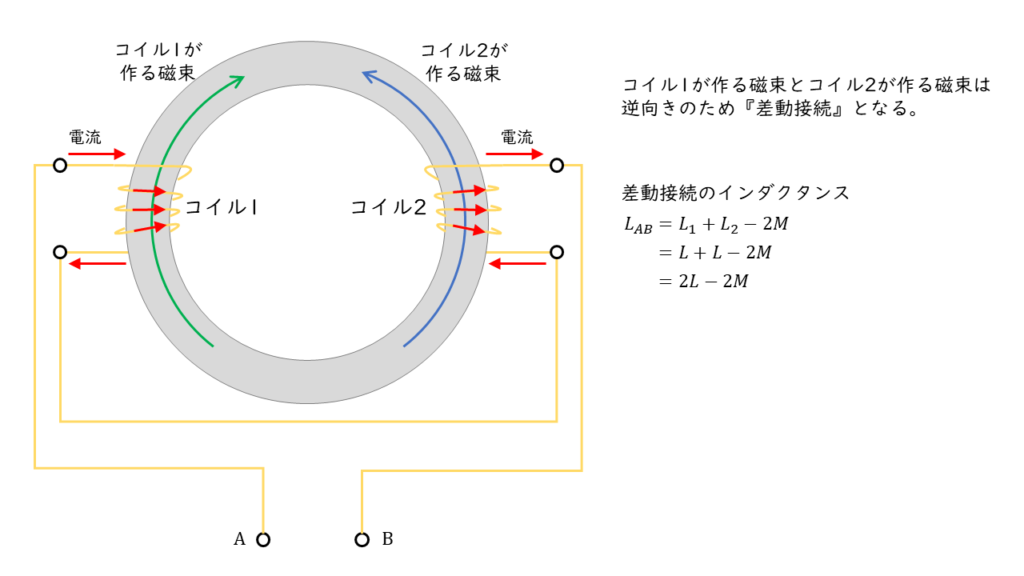
差動接続…下図のように各コイルの作る磁界が逆向きになり,磁束を打ち消しあうような接続方法です。
問題文には,「2つのコイルを接続した場合,それぞれの自己インダクタンスの合計よりも大きくなった」と記載があるので,「和動接続」と考えられます。











コメント