問題
極板間が比誘電率 \(ε_r\) の誘電体で満たされている平行平板コンデンサに一定の直流電圧が加えられている。このコンデンサに関する記述 a~e として,誤っているものの組合せを次の(1)~(5)のうちから一つ選べ。
ただし,コンデンサの端効果は無視できるものとする。
a. 極板間の電界分布は \(ε_r\) に依存する。
b. 極板間の電位分布は \(ε_r\) に依存する。
c. 極板間の静電容量は \(ε_r\) に依存する。
d. 極板間に蓄えられる静電エネルギーは \(ε_r\) に依存する。
e. 極板上の電荷(電気量)は \(ε_r\) に依存する。
(1) a,b
(2) a,e
(3) b,c
(4) a,b,d
(5) c,d,e
解説
答え:(1)
a. 極板間の電界分布は \(ε_r\) の関係について
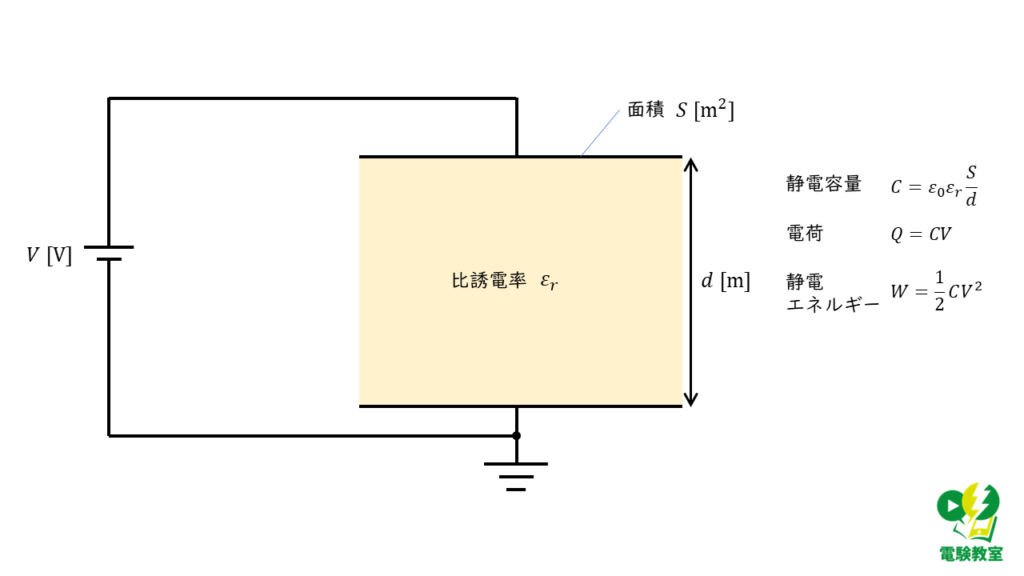
問題文の回路を図に表すと,図1のように示すことができます。
直流電源から一定の電圧が印加されているコンデンサ内部の電界\(E\) [V/m]は,
\( E = \displaystyle \frac{V}{d}\)
で表すことができ,コンデンサ内部は「平等電界」となるので,電界分布は誘電率\(ε_r\)に依存しません。
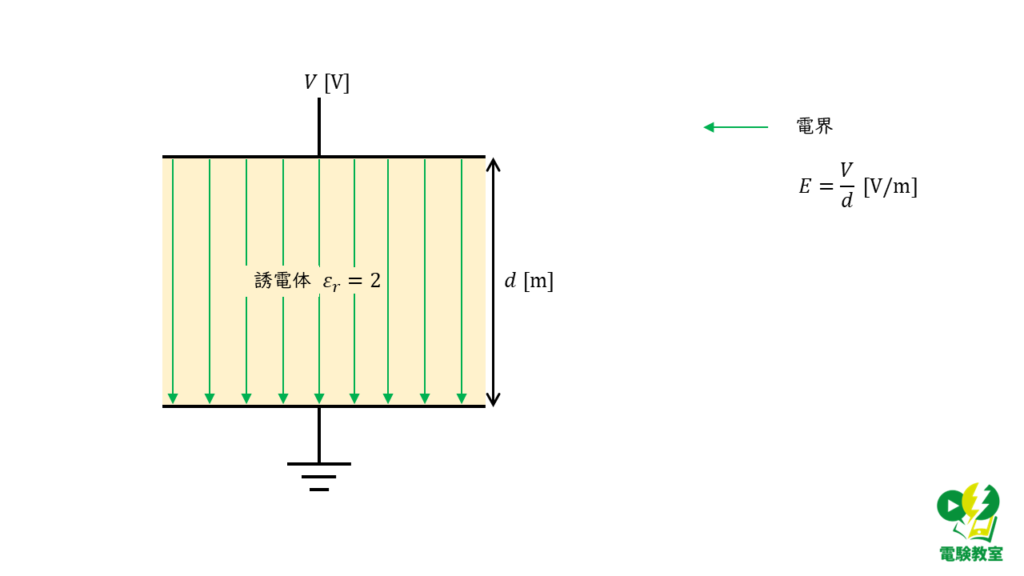
選択肢aは誤り
b. 極板間の電位分布は \(ε_r\) について
平行平板コンデンサには一定の直流電圧\( V\) [V] が印加されているため,電界分布が一様となるので,電位分布も一様となります。したがって,極板間の電位分布は\(ε_r\) に依存しません。
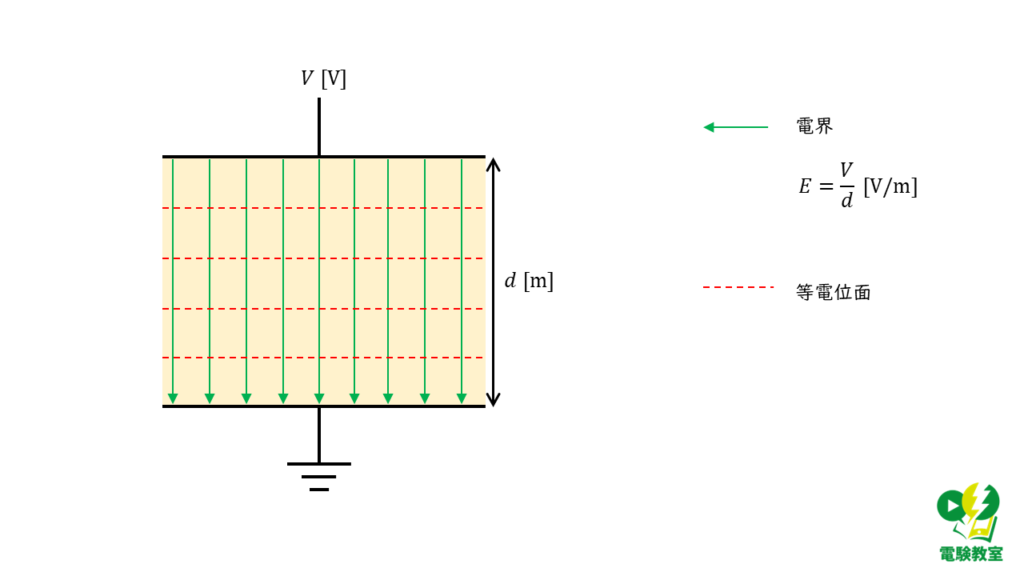
選択肢bは誤り
c. 極板間の静電容量は \(ε_r\) について
平行平板コンデンサの極板面積を\(S \ \rm [m^2]\),極板間距離を\( d \ \rm [m]\),真空中の誘電率を\(ε_0 \ \rm [F/m] \),比誘電率を\(ε_r \)とすると静電容量\(C \ \rm [F]\)は,
\( C = ε_0 ε_r \displaystyle \frac{S}{d} \)
と表すことができ、比誘電率\( ε_r\)に依存することが分かります。
d. 極板間に蓄えられる静電エネルギーは \(ε_r\) について
平行平板コンデンサの静電エネルギー\(W\) [J]は,静電容量を\( C\) [F],電源電圧を\(V\) [V]とすると,
\( W = \displaystyle \frac{1}{2} C V^2 \)
で表すことができます。静電容量\(C\)は,比誘電率\(ε_r\)に依存する値であるため,静電エネルギーも比誘電率\(ε_r\)に依存するといえます。
e. 極板上の電荷(電気量)は \(ε_r\) について
極板上に蓄えられる電荷\(Q\) [C]は,静電容量\(C\) [F]と電源電圧\(V\) [V]を用いて,
\( Q = CV\)
で表すことができます。静電容量\(C\)は,誘電率\(ε_r\)に依存する値であるため,極板上の電荷も比誘電率\(ε_r\)に依存するといえます。











コメント