【過去問解説】H25理論　問3　磁界と磁束に関する選択問題

問題

磁界及び磁束に関する記述として，誤っているものを次の(1)～(5)のうちから一つ選べ。

(1)　 \(1\ \rm[m]\) 当たりの巻数が \(N\) の無限に長いソレノイドに電流 \(I\ \rm[A]\) を流すと，ソレノイドの内部には磁界 \(H = NI \ \rm[A/m]\) が生じる。磁界の大きさは，ソレノイドの寸法や内部に存在する物質の種類に影響されない。

(2)　均一磁界中において，磁界の方向と直角に置かれた直線状導体に直流電流を流すと，導体には電流の大きさに比例した力が働く。

(3)　 \(2\) 本の平行な直線状導体に反対向きの電流を流すと，導体には導体間距離の \(2\) 乗に反比例した反発力が働く。

(4)　フレミングの左手の法則では，親指の向きが導体に働く力の向きを示す。

(5)　磁気回路において，透磁率は電気回路の導電率に，磁束は電気回路の電流にそれぞれ対応する。

解説

答え：（3）

ソレノイドの作る磁界

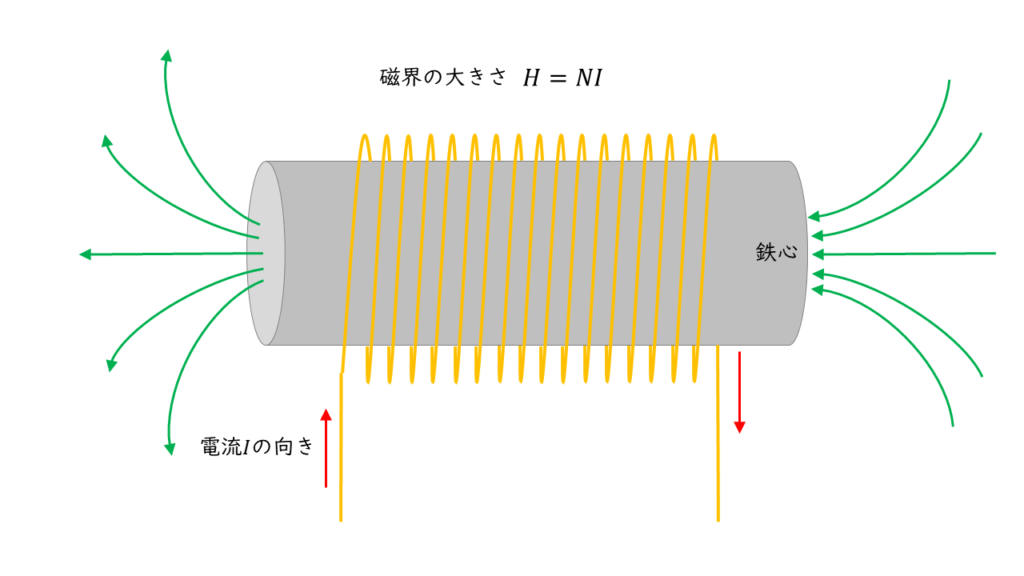
上図のように無限に長いソレノイドの作る磁界の大きさ \( H \ \rm[A/m]\) は，

\( H = NI \)

で表すことができ，発生する磁界の大きさは，ソレノイドの寸法や内部の鉄心などの材質に影響を受けません。よって、「(1)は正しい」といえます。

磁界中に置かれた直線導体にはたらく電磁力

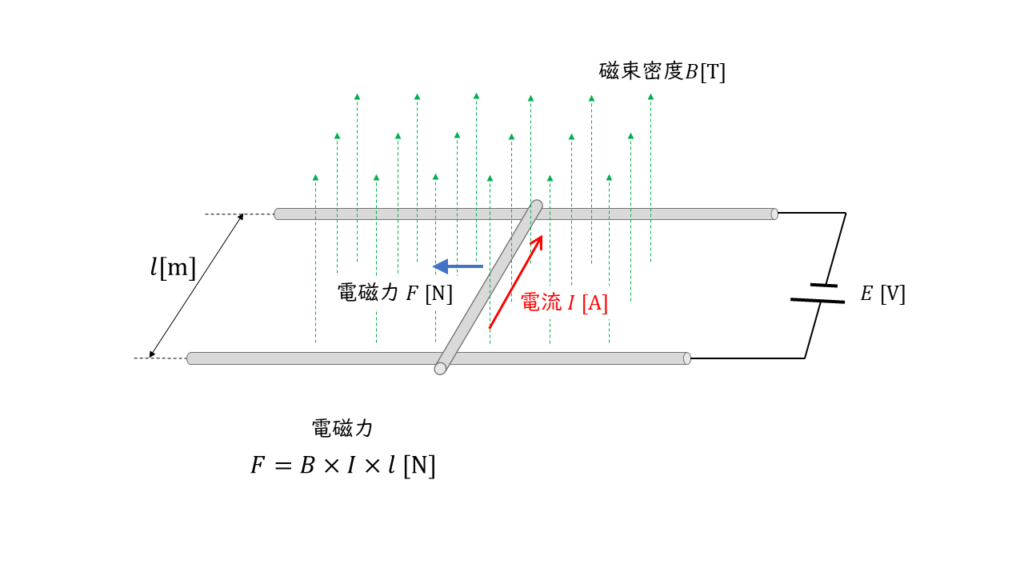
上図のように磁束密度 \(B\ \rm[T]\) の磁界中に置かれた直線導体に，電流 \(I\ \rm[A]\) を流すと，\(l\ \rm m\)の導体にはたらく電磁力 \(F\ \rm [N]\) の大きさは，

\( F = BIl \ \rm[N]\)

で表されます。この式から，電磁力が電流の大きさに比例することが分かるので，「(2)も正しい」といえます。

2本の平行な直線導体にはたらく電磁力

2本の平行な直線導体に互いに反対向きに電流を流した場合，それぞれの電流の作る磁界は下図のようになります。

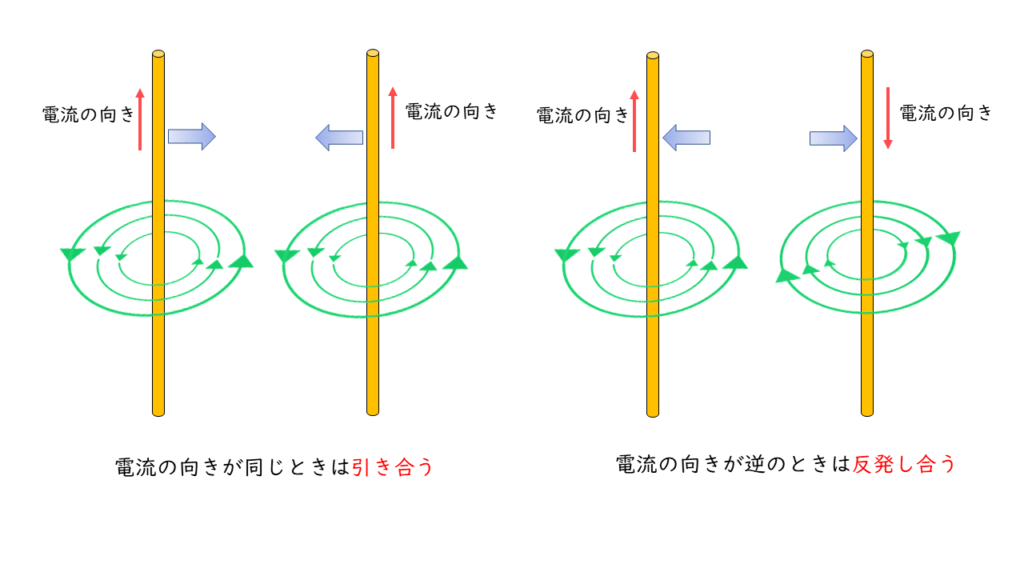
フレミングの左手の法則より，各直線導体にはたらく力の向きは，互いに反発する方向に働きます。
したがって，「(3)は誤り」であることが分かります。

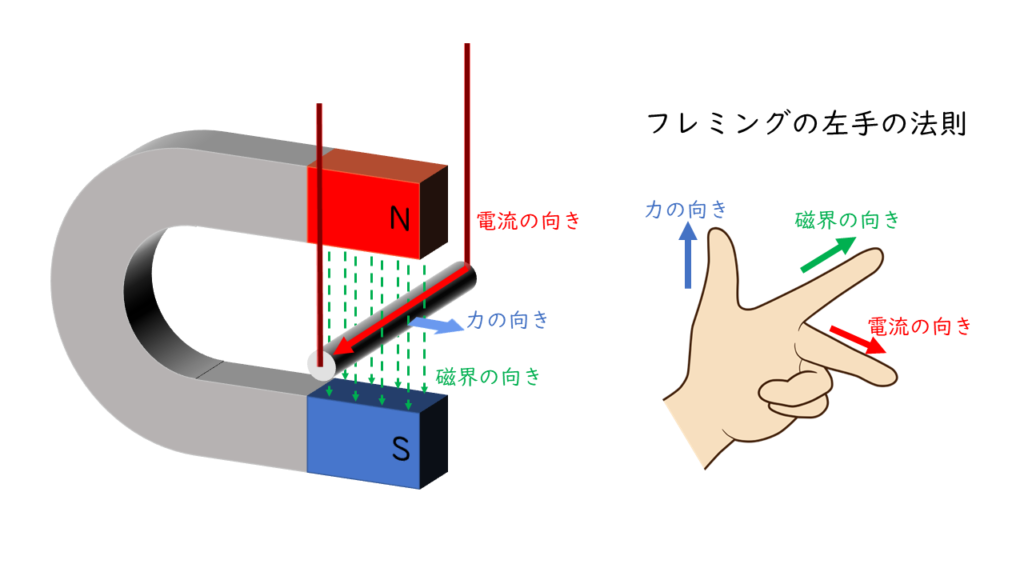
フレミングの左手の法則

フレミングの左手の法則は，磁界中にある導体に電流を流した時に，導体にはたらく力の向きと電流，磁界の向きの関係を表したものです。下図より「(4)も正しい」ことが分かります。

電気回路と磁気回路の比較

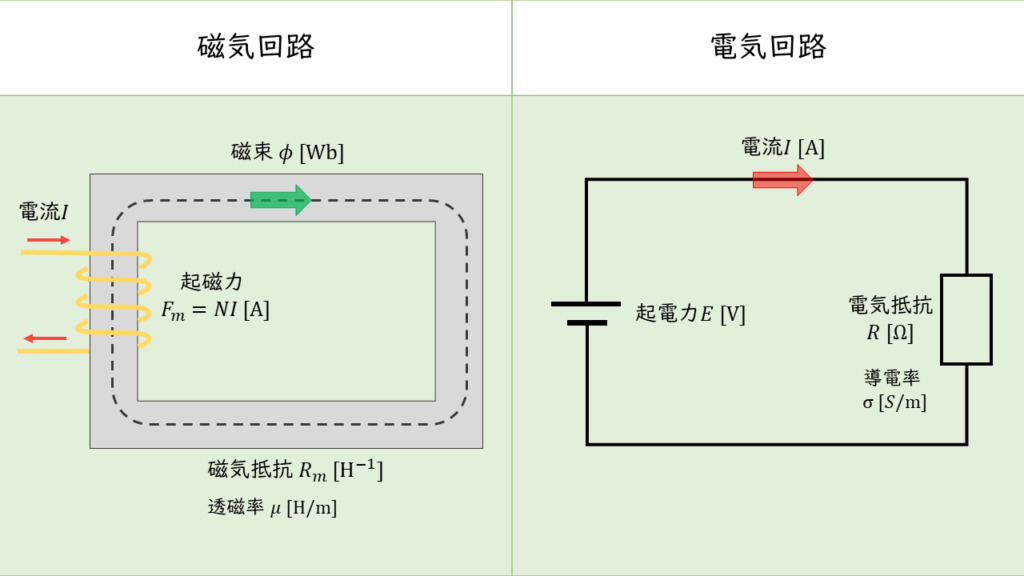
上図から分かるように磁気回路と電気回路は同じように考えることができ，それぞれ以下のように対応しています。

電気回路	磁気回路
電圧 \(E \ \rm[V]\)	起磁力 \(NI \ \rm[A]\)
電流 \(I \ \rm [A]\)	磁束 \( \phi \ \rm[Wb]\)
抵抗 \( R \ \rm [\Omega]\)	磁気抵抗 \( R_m \ \rm[H^{-1}]\)
導電率 \( \sigma \ \rm [S/m]\)	透磁率 \( \mu \ \rm [H/m[\)

電気回路と磁気回路の比較から「(5)も正しい」といえます。