問題
極板A−B間が比誘電率\(ε_r = 2\)の誘電体で満たされた平行平板コンデンサがある。極板間の距離は\(d\) [m],極板間の直流電圧は\(V_0\) [V]である。極板と同じ形状と大きさをもち,厚さが\(\displaystyle \frac{d}{4}\) [m]の帯電していない導体を図に示す位置P−Q間に極板と平行に挿入したとき,導体の電位の値[V]として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,コンデンサの端効果は無視できるものとする。
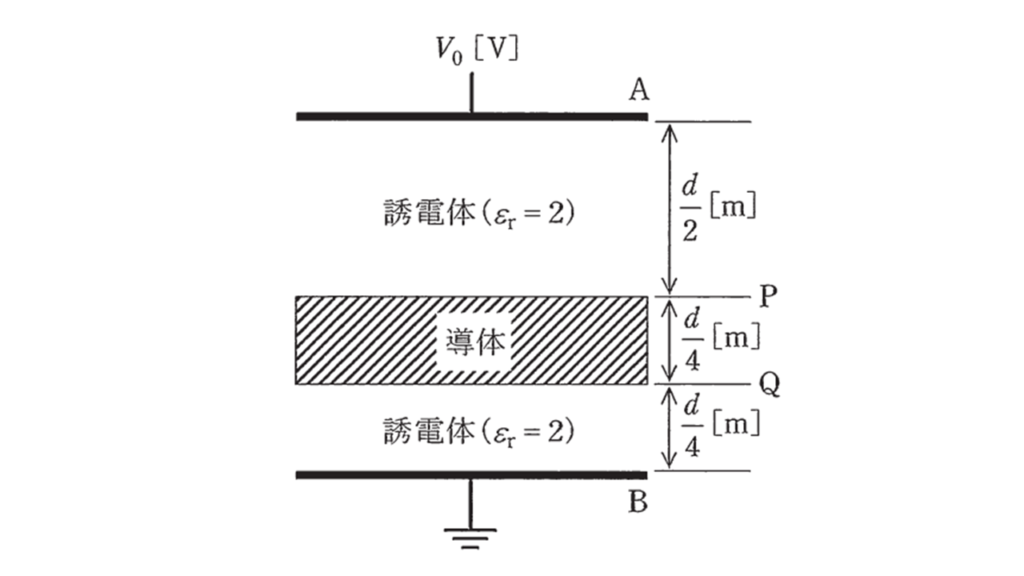
(1) \(\displaystyle \frac{V_0}{8}\) (2) \(\displaystyle \frac{V_0}{6}\) (3) \(\displaystyle \frac{V_0}{4}\) (4) \(\displaystyle \frac{V_0}{3}\) (5) \(\displaystyle \frac{V_0}{2}\)
解説
答え:(4)
導体挿入前のコンデンサ内の電界を求める
導体を挿入する前のコンデンサは図2のように表すことができます。
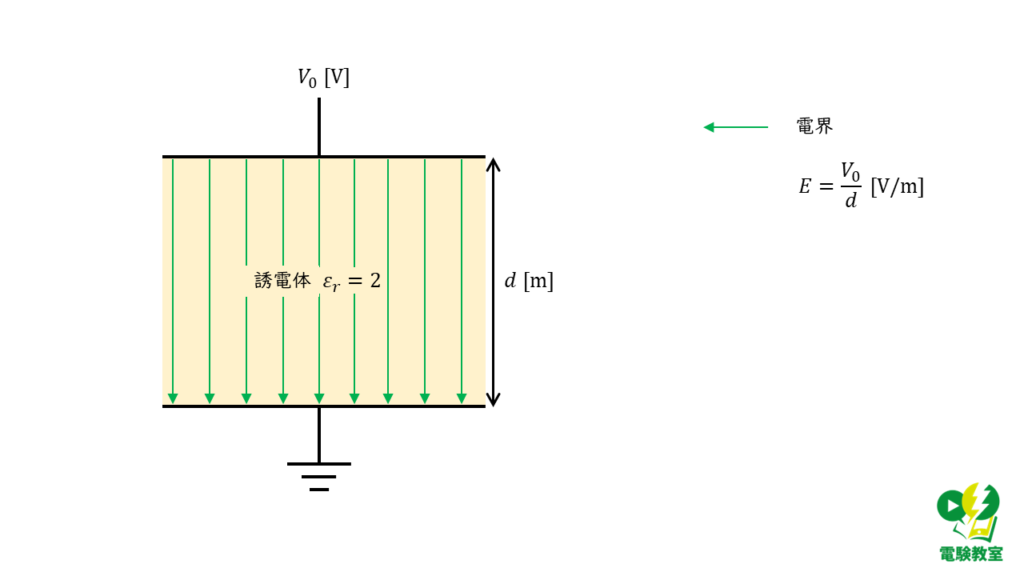
図2より、コンデンサ内部の電界の大きさ\(E\) [V/m]は,
\( E = \displaystyle \frac{V_0}{d}\)
と表すことができます。
導体挿入後の誘電体内の電界を求める
帯電していない導体をコンデンサ内部に挿入した場合,図3のように極板間距離の異なる2つのコンデンサが直列に接続されているとみなすことができます。
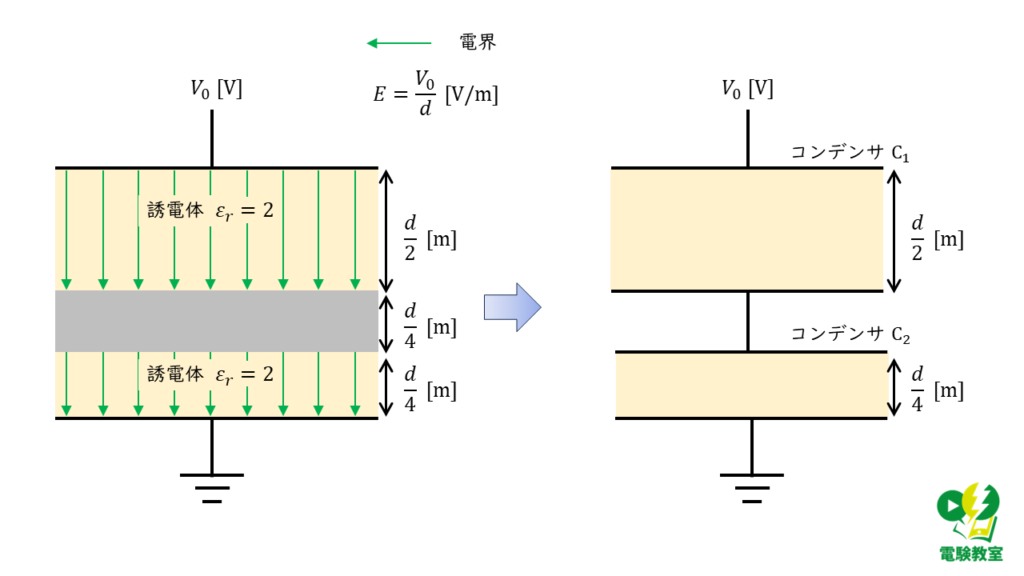
図3より,コンデンサ\(\rm C_1\),\(\rm C_2\)の内部の電界の大きさは,電源電圧の大きさが変化しないことから,
\( E_1 = E_2 = E \) [V/m]
となります。
コンデンサ\(\rm C_1\),\(\rm C_2\)の両端の電位を求める
電界と電位は\( E = \displaystyle \frac{V}{d}\)の関係にあるので,コンデンサ\(\rm C_1\),\(\rm C_2\)の電位\(V_1\),\(V_2\)は,
\( V_1 = E_1 \times \displaystyle \frac{d}{2} = \displaystyle \frac{Ed}{2} \)
\( V_2 = E_2 \times \displaystyle \frac{d}{4} = \displaystyle \frac{Ed}{4} \)
\( V_1 = 2 V_2 \)
と表すことができます。電位の大きさは,
\( V_0 = V_1 +V_2 \)
の関係にあるので,
\(\begin{align} V_0 &= V_1 +V_2 \\ \\ &= 2V_2 +V_2 \\ \\ V_2 &= \displaystyle \frac{1}{3} V_0 \end{align} \)
\( V_1 = 2V_2 = \displaystyle \frac{2}{3}V_0 \)
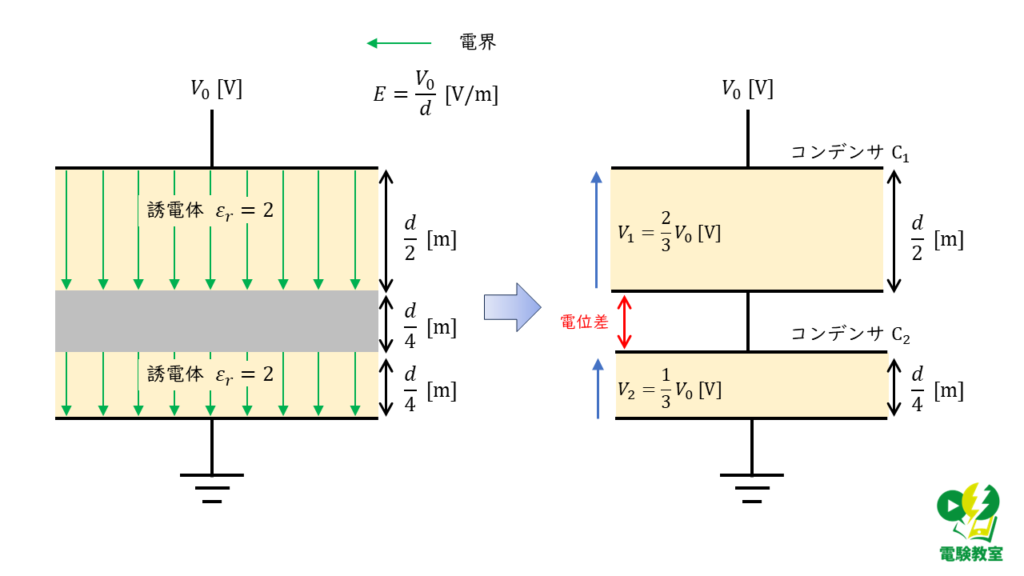
したがって,コンデンサ\(\rm C_1\),\(\rm C_2\)間の電位差(導体の電位)は,
\( V_1 – V_2 = \displaystyle \frac{2}{3}V_0 – \displaystyle \frac{1}{3}V_0 = \displaystyle \frac{1}{3}V_0 \) [V]
よって,答えは(4)となります。











コメント