問題
次の文章は,ある強磁性体の初期磁化特性について述べたものである。
磁界の向きに強く磁化され,比透磁率 \(μ_r\) が \(1\) よりも非常に \( \fbox{ (ア) } \) 物質を強磁性体という。まだ磁化されていない強磁性体に磁界 \(H\ \rm[A/m]\) を加えて磁化していくと,磁束密度 \(B\ \rm[T]\) は図のように変化する。よって,透磁率 \(μ\ \rm[H/m] \left( = \displaystyle \frac{\mathit{B}}{\mathit{H}} \right) \) も磁界の強さによって変化する。図から,この強磁性体の透磁率 \(μ\) の最大値はおよそ \(μ_{max} = \ \fbox{ (イ) } \ \rm H/m \) であることが分かる。このとき,強磁性体の比透磁率はほぼ \(μ_r = \fbox{ (ウ) } \) である。点 \(P\) 以降は磁界に対する磁束密度の増加が次第に緩くなり,磁束密度はほぼ一定の値となる。この現象を\( \fbox{ (エ) } \) という。
ただし,真空の透磁率を \(μ_0 = 4 \pi \times 10^{-7} \ \rm H/m\) とする。
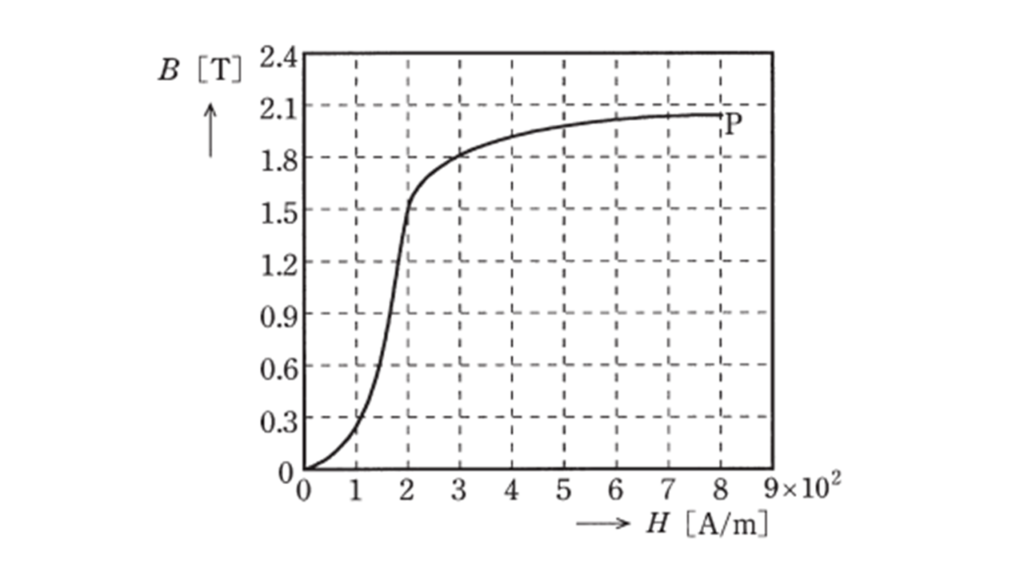
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{lllll} \ &(ア)& (イ)& (ウ)& (エ)\\ \hline (1) &大きい &7.5 \times 10^{-3} &6.0 \times 10^{3} &磁気飽和 \\ \hline (2) &小さい &7.5 \times 10^{-3} &9.4 \times 10^{-9} &残留磁気 \\ \hline (3) &小さい &1.5 \times 10^{-2} &9.4 \times 10^{-9} &磁気遮へい \\ \hline (4) &大きい &7.5 \times 10^{-3} &1.2 \times 10^{4} &磁気飽和 \\ \hline (5) &小さい &1.5 \times 10^{-2} &1.2 \times 10^{4} &残留磁気 \\ \hline \end{array} $$
解説
答え:(1)
強磁性体とは
比透磁率 \(μ_r\) よりも非常に『大きい』物資のことを強磁性体と呼びます。
代表的な物質としては,鉄,コバルト,ニッケルなどがあります。
磁界と磁束密度の関係
問のグラフを見ると,磁界の大きさ \( H = 2.0 \ \rm[A/m]\) を境にグラフの傾きが大きく変化していることが読み取れます。
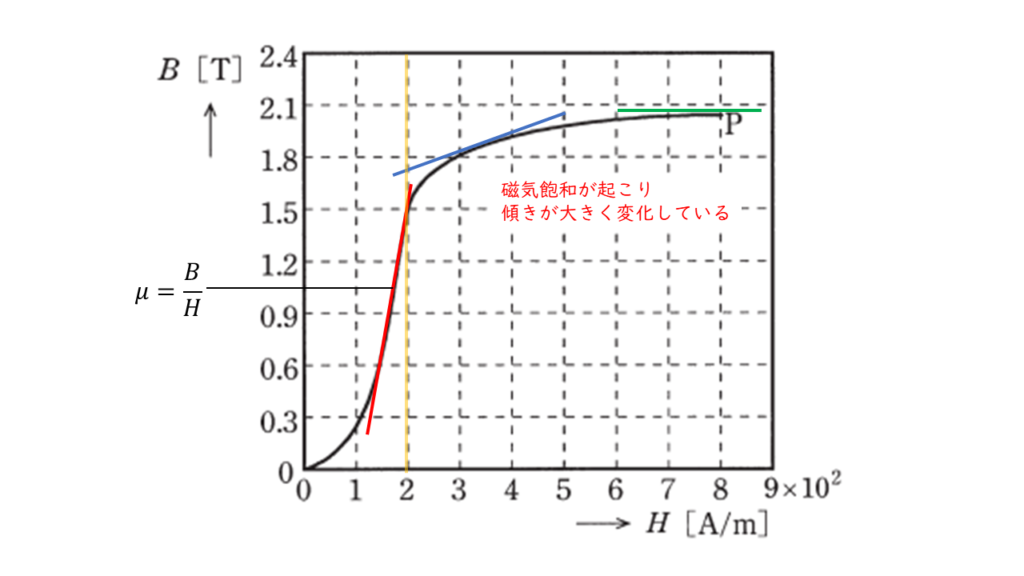
これは,磁界の大きさが \( 2.0 \ \rm A/m\) より大きくなると『磁気飽和』により,磁界の大きさ \(H\) と磁束密度 \(B\) が比例しなくなることを表しています。
問題文より,透磁率 \(μ\) は,磁界の大きさと磁束密度の関係式
\( μ = \displaystyle \frac{B}{H} \)
で変化すると記載があるので,透磁率の最大値は,
\( μ_{max} = \displaystyle \frac{1.5\ \rm T}{2.0 \times 10^{2} \ \rm A/m} = 7.5 \times 10^{-3} \)
比透磁率を計算する
透磁率 \(\mu\) ,真空中の透磁率 \(\mu _0\) ,比透磁率 \(\mu _r\) は,以下の関係式で表されます。
\( \mu =\mu _r \times \mu _0\)
上記の式を用いて,透磁率が最大となった時の値から比透磁率を計算すると,
\(\begin{align} \mu _{max} &= \mu _r \times \mu _0 \\ \\ 7.5 \times 10^{-3} &= 4 \pi \times 10^{-7} \times \mu _r \\ \\ \mu _r &= \displaystyle \frac{7.5 \times10^{-3}}{4 \pi \times 10^{-7}} = 6.0 \times 10^3 \end{align} \)
磁気飽和
磁界に対する磁束密度の増加が次第に緩くなり,磁束密度はほぼ一定の値となる現象を『磁気飽和』といいます。











コメント