問題
図のように,長い線状導体の一部が点 \(P\) を中心とする半径 \(r\ \rm[m]\) の半円形になっている。この導体に電流 \(I\ \rm[A]\) を流すとき,点 \(P\) に生じる磁界の大きさ \(H\ \rm[A/m]\) はビオ・サバールの法則より求めることができる。 \(H\) を表す式として正しいものを,次の(1)~(5)のうちから一つ選べ。
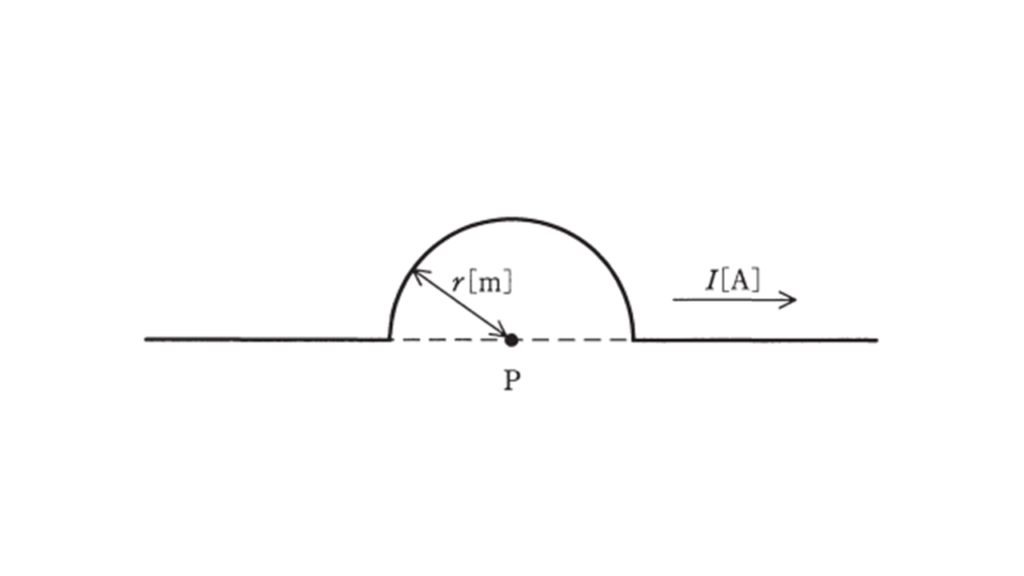
(1) \(\displaystyle \frac{I}{2 \pi r}\) (2) \(\displaystyle \frac{I}{4r}\) (3) \(\displaystyle \frac{I}{\pi r}\) (4) \(\displaystyle \frac{I}{2r}\) (5) \(\displaystyle \frac{I}{r}\)
解説
答え:(2)
ビオバザールの法則とは
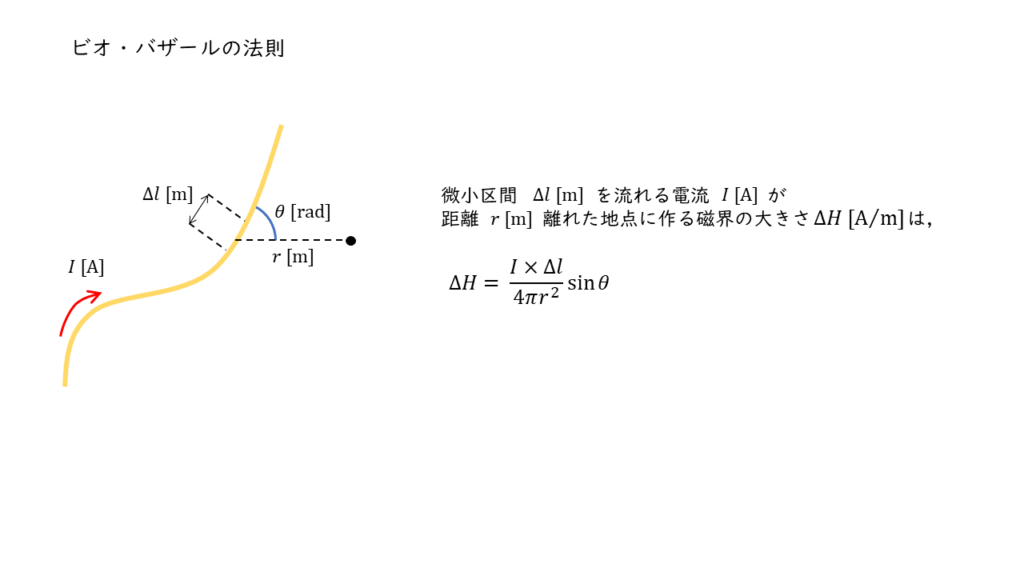
上図のように,微小な長さ \(\Delta l\ \rm m\) に電流 \(I \ \rm A\) が流れた場合,距離 \(r\ \rm m\) 離れた場所に電流が作る磁界 \(\Delta H\ \rm [A/m]\) の大きさは,
\( \Delta H = \displaystyle \frac{I \ \Delta l}{4 \pi r^2} \sin \theta \)
で表されます。
円形コイルを流れる電流が作る磁界

上図にビオ・バザールの法則をあてはめると,
\(\begin{align} H &= \displaystyle \frac{N2\pi r}{4 \pi r^2} \sin \displaystyle \frac{\pi}{2}\\ \\ &= \displaystyle \frac{I}{2r} \end{align} \)
問の図では,導体は円の半分なので,磁界の大きさは,
\(\begin{align} H’ &= H \times \displaystyle \frac{1}{2} \\ \\ &= \displaystyle \frac{I}{2r} \times \displaystyle \frac{1}{2} \\ \\ &= \displaystyle \frac{I}{4r} \end{align} \)
よって,答えは(2)となります。











コメント