問題
次の文章は,抵抗器の許容電力に関する記述である。
許容電力 \(\displaystyle \frac{1}{4}\ \rm W\) ,抵抗値 \(100\ \Omega\) の抵抗器 \(\rm A\) ,及び許容電力 \(\displaystyle \frac{1}{8}\ \rm W\) ,抵抗値 \(200\ \Omega\) の抵抗器 \(\rm B\) がある。抵抗器 \(\rm A\) と抵抗器 \(\rm B\) とを直列に接続したとき,この直列抵抗に流すことのできる許容電流の値は\(\fbox{(ア)}\) \(\rm mA\) である。また,直列抵抗全体に加えることのできる電圧の最大値は,抵抗器 \(\rm A\) と抵抗器 \(\rm B\) とを並列に接続した時に加えることのできる電圧の最大値の \(\fbox{(イ)}\) 倍である。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる数値の組合せとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
\(\begin{array}{ccccc} \ &(ア)&(イ)\\ \hline (1) & 25.0 &1.5 \\ \hline (2) &25.0 &2.0 \\ \hline (3) &37.5 &1.5 \\ \hline (4) &50.0 &0.5 \\ \hline (5) &50.0 &2.0 \\ \hline \end{array} \)
解説
答え:(1)
各抵抗器の許容電流の値を求める
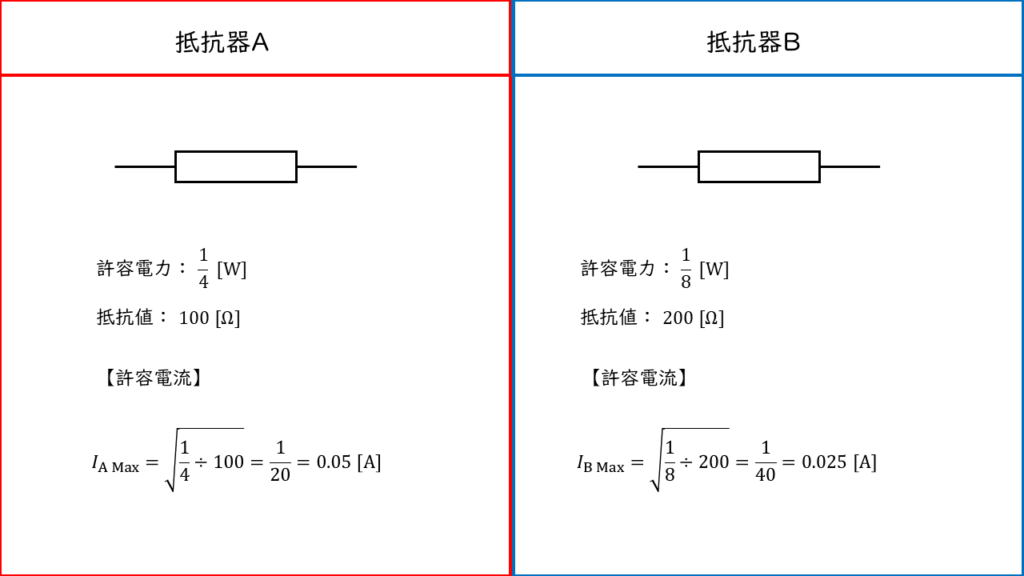
抵抗器 \(\rm A,B\) の許容電流は,許容電力と抵抗値の値から以下の式で計算することができます。
\(\begin{align} 許容電力 &= 抵抗値 \times \left( 許容電流の二乗 \right) \\ \\ P_{Max} &= R \times I_{Max} ^2 \end{align} \)
よって各抵抗器の許容電流 \(I_{A\ Max}\) ,\(I_{B\ Max}\) の大きさは,
\(\begin{align} I_{A\ Max}^2 &= \displaystyle \frac{1}{4} \div 100 \\ \\ &= \displaystyle \frac{1}{400} \\ \\ I_{A\ Max} &= \displaystyle \frac{1}{20} \\ \\ &=0.05\ \rm [A] \rightarrow 50\ \rm[mA] \end{align}\)
\(\begin{align} I_{B\ Max}^2 &= \displaystyle \frac{1}{8} \div 200 \\ \\ &= \displaystyle \frac{1}{1600} \\ \\ I_{B\ Max} &= \displaystyle \frac{1}{40} \\ \\ &= 0.025\ \rm [A] \rightarrow 25\ \rm[mA] \end{align}\)
2つの抵抗器を直列につないだ場合
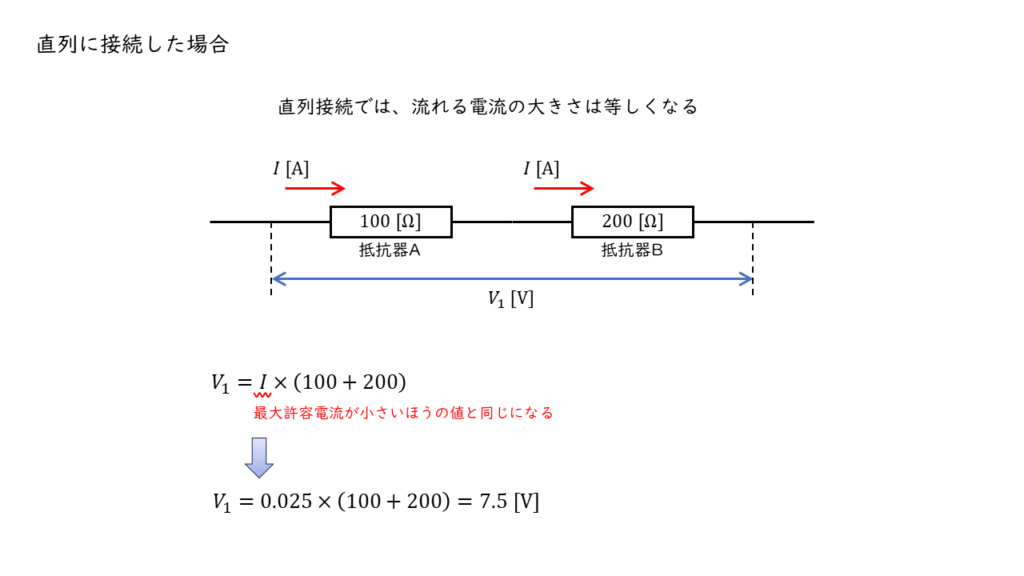
直列接続されている部分に流れる電流の大きさは等しくなるため,抵抗器 \(\rm A,B\)に流すことができる最大電流は,許容電流の小さい抵抗器 \(\rm B\) の許容電流 \(25.0\ \rm [A]\)と等しくなります。
電流が,\(I_{Max} = 0.025\ \rm A\) のとき抵抗器の両端に現れる電圧 \(V_1 \ \rm [V]\) は,
\(\begin{align} V_1 &= I_{Max} \times \left(R_A + R_B \right) \\ &= 0.025 \times \left( 100 + 200 \right) \\ &= 7.5\ \rm [V] \end{align} \)
2つの抵抗器を並列につないだ場合
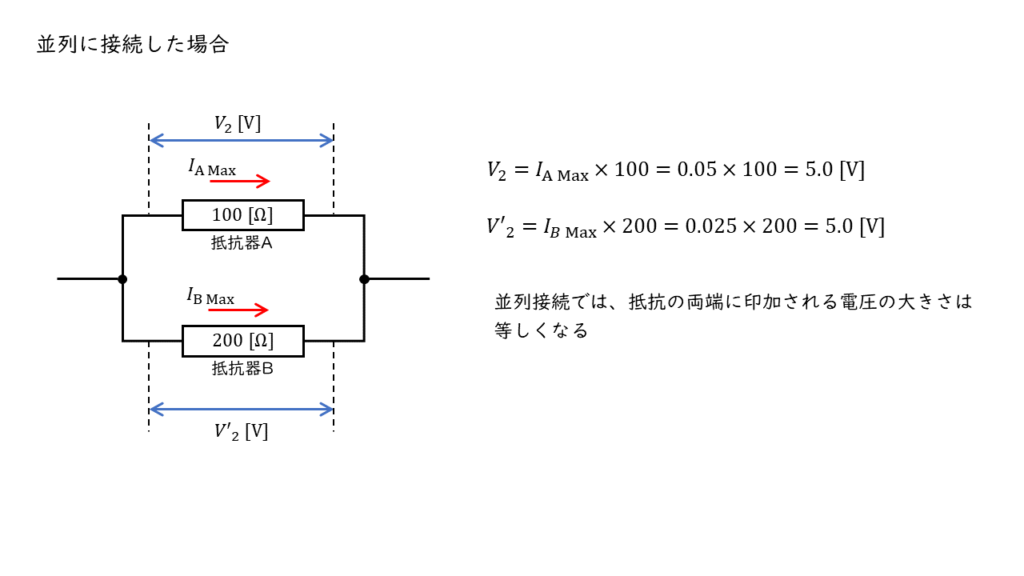
抵抗を並列に接続した場合,それぞれの抵抗の両端には同じ大きさの電圧が現れます。両端の電圧の大きさを \(V_2\ \rm[V]\) とすると,オームの法則より抵抗に流れる電流は,
\(\begin{align} I_{A\ Max} &= \displaystyle \frac{V_2}{100} \tag{1} \end{align}\)
\(\begin{align} I_{B\ Max} &= \displaystyle \frac{V’_2}{200} \tag{2} \end{align}\)
2つの式から得られる電圧の値を比較し,低い電圧が並列接続した場合に抵抗の両端に印加することができる電圧の最大値となります。
式(1),(2)を計算すると,
\(\begin{align} I_{A\ Max} &= \displaystyle \frac{V_2}{100} \\ \\ 0.05 &= \displaystyle \frac{V_2}{100} \\ \\ V_2 &= 0.05 \times 100 \\ \\ &= 5\ \rm[V] \end{align}\)
\(\begin{align} I_{B\ Max} &= \displaystyle \frac{V’_2}{200} \\ \\ 0.025 &= \displaystyle \frac{V’_2}{200} \\ \\ V’_2 &= 0.025 \times 200 \\ \\ &= 5\ \rm[V] \end{align}\)
となり,\(V_2 = V’_2 = 5\ \rm V\)なので,抵抗に印加できる最大の電圧は,\(5\ \rm[V]\) と求めることができます。
接続方法による印加電圧の最大値を比較する
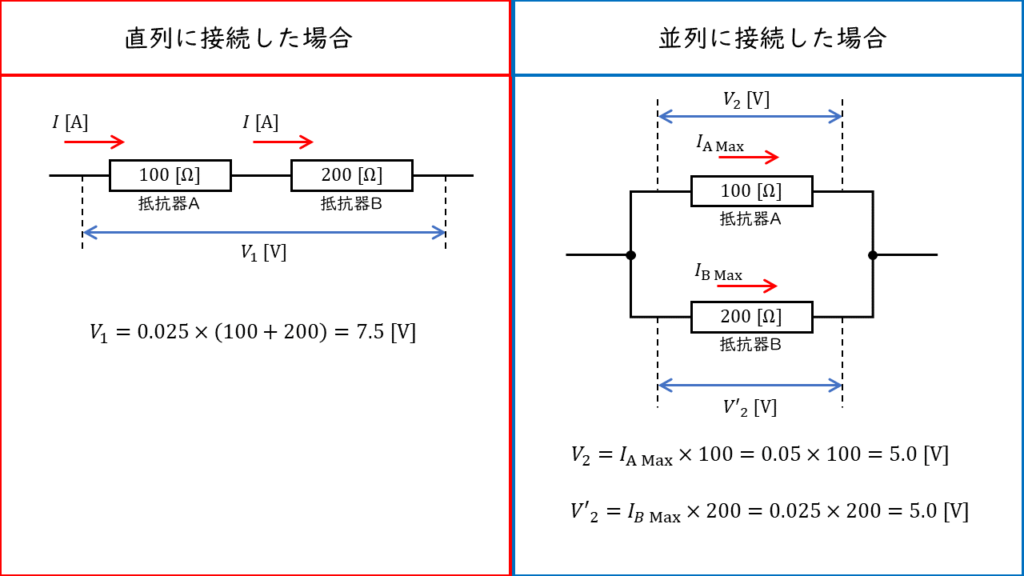
直列接続と並列接続で印加できる電圧の最大値を比較すると,
\(\begin{align} \displaystyle \frac{直列接続時の最大印加電圧}{並列接続時の最大印加電圧} &= \displaystyle \frac{V_1}{V_2} \\ \\ &= \displaystyle \frac{7.5}{5} \\ \\ &= 1.5 \end{align} \)
以上のことから,問の答えは(1)となります。










