【過去問解説】　H30理論　問6　抵抗のみの直流回路の計算問題

問題

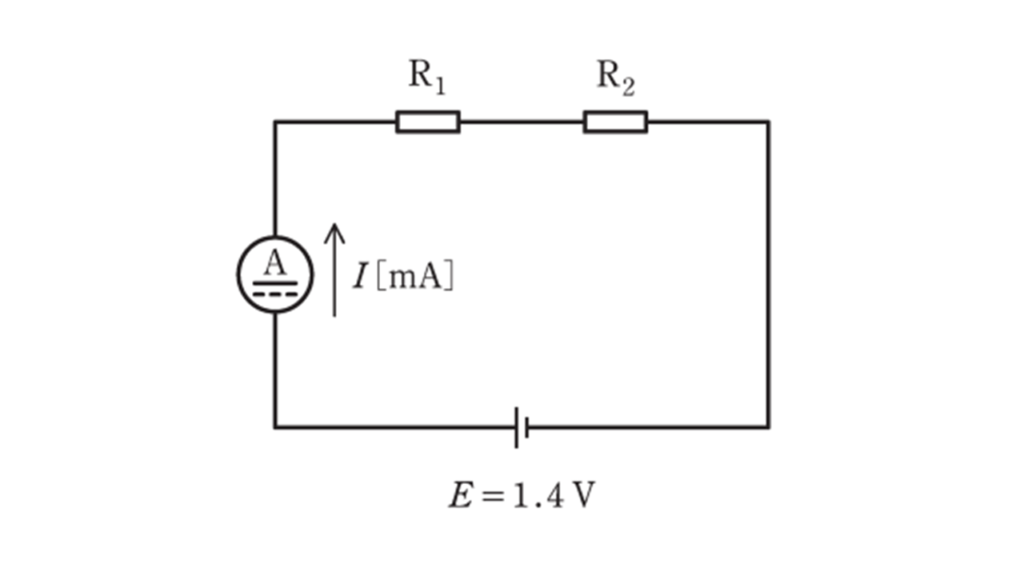
\(\rm R_a，R_b\) 及び\(\rm R_c\) の三つの抵抗器がある。これら三つの抵抗器から二つの抵抗器( \(\rm R_1\) 及び \(\rm R_2\) )を選び，図のように，直流電流計及び電圧 \(E=1.4\ \rm V\)の直流電源を接続し，次のような実験を行った。

　実験Ⅰ：\(\rm R_1\) を \(\rm R_a\) ，\(\rm R_2\) を \(\rm R_b\) としたとき、電流 \(I\) の値は \(56\ \rm mA\) であった。
　実験Ⅱ：\(\rm R_1\) を \(\rm R_b\)，\(\rm R_2\) を \(\rm R_c\) としたとき、電流 \(I\) の値は \(35\ \rm mA\) であった。
　実験Ⅲ：\(\rm R_1\) を \(\rm R_a\) ，\(\rm R_2\) を \(\rm R_c\) としたとき、電流 \(I\) の値は \(40\ \rm mA\) であった。

これらのことから，\(R_b\) の抵抗値[\(\Omega\)]として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，直流電源及び直流電流計の内部抵抗は無視できるものとする。

(1)　\(10\)　　(2)　\(15\)　　(3)　\(20\)　　(4)　\(25\)　　(5)　\(30\)

解説

答え：(2)

実験Ⅰ～Ⅲの結果から式を立てる

オークの法則より，実験Ⅰ～Ⅲの各条件における式を立てると以下のようになります。

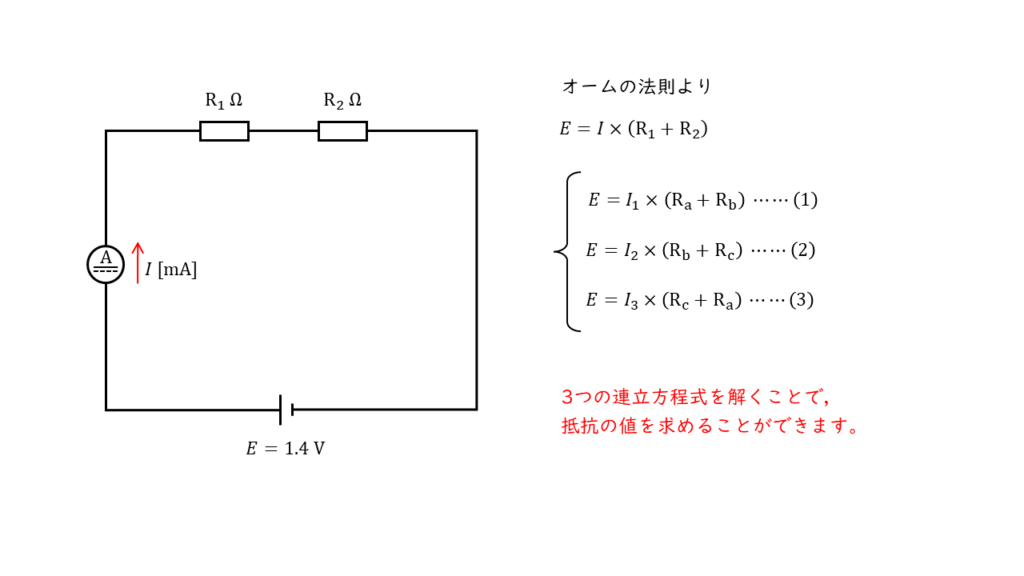
実験Ⅰの結果より

\(\begin{align} E &= I_1 \times \left( \rm R_a + R_b \right) \\ \\ \color{red}{1.4} &= \color{red}{0.056} \times \left( \rm R_a + R_b \right) \\ \\ \left( \rm R_a + R_b \right) &= \displaystyle \frac{1.4}{0.056} \\ \\ \rm R_a + R_b &= 25\ \cdots \cdots \left(1\right) \end{align} \)

実験Ⅱの結果より

\(\begin{align} E &= I_2 \times \left( \rm R_b + R_c \right) \\ \\ \color{red}{1.4} &= \color{red}{0.035} \times \left( \rm R_b + R_c \right) \\ \\ \left( \rm R_b + R_c \right) &= \displaystyle \frac{1.4}{0.035} \\ \\ \rm R_b + R_c &= 40\ \cdots \cdots \left(2\right) \end{align} \)

実験Ⅲの結果より

\(\begin{align} E &= I_3 \times \left( \rm R_c + R_a \right) \\ \\ \color{red}{1.4} &= \color{red}{0.04} \times \left( \rm R_c + R_a \right) \\ \\ \left( \rm R_c + R_a \right) &= \displaystyle \frac{1.4}{0.04} \\ \\ \rm R_c + R_a &= 35\ \cdots \cdots \left(3\right) \end{align} \)

よって以下の3つの連立方程式を得ることができました。

連立方程式を解く

式 \( \left( 3 \right) – \left( 1 \right) \) より，

\(\begin{align}\rm R_a + R_c &= 35 \\ – \ ) \ \rm R_a + R_b &= 25 \\ \hline \rm R_c \color{red}{-} R_b &= 10 \cdots \cdots \left(4\right) \end{align} \)

式 \( \left( 2 \right) – \left( 4 \right) \) より，

\(\begin{align}\rm R_b + R_c &= 40 \\ – \ ) \ \rm -R_b + R_c &= 10 \\ \hline \rm \color{red}{2R_b } &= 30 \\ \rm R_b &= 15 \end{align} \)

したがって，答えは(2)となります。