【過去問解説】R1年理論　問1　点電荷の電位に関する選択問題

問題

　図のように，真空中に点P，点A，点B，が直線上に配置されている。点Pは\(Q\ [C]\)の点電荷を置いた点とし，A-B間に生じる電位差の絶対値を\(|V_{AB}|\ [V]\)とする。次の(a)～(d)の四つの実験を個別に行ったとき，\(|V_{AB} \ [V]\)の値が最小となるものと最大となるものの実験の組み合わせとして，正しい物を次の(1)～(5)のうちから一つ選べ。

[実験内容]
(a) P-A間の距離を\(2\ m\)，A-B間の距離を\(1\ m\)とした。
(b) P-A間の距離を\(1\ m\)，A-B間の距離を\(2\ m\)とした。
(c) P-A間の距離を\(0.5\ m\)，A-B間の距離を\(1\ m\)とした。
(d) P-A間の距離を\(1\ m\)，A-B間の距離を\(0.5\ m\)とした。

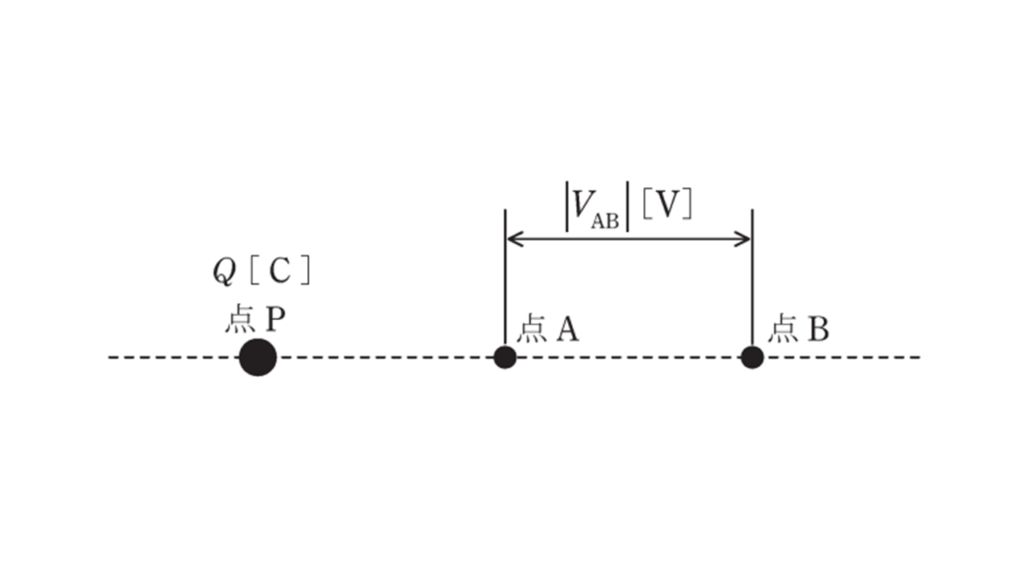
(1) (a)と(b)　(2) (a)と(c)　(3) (a)と(d)　(4) (b)と(c)　(5) (c)と(d)

解説

答え：(1)

点電荷の作る電位の公式\(V = \displaystyle \frac{Q}{4 \pi εr}\)に各条件を代入して点A，点Bにおける電位計算し、A-B間の電位差を求めます。

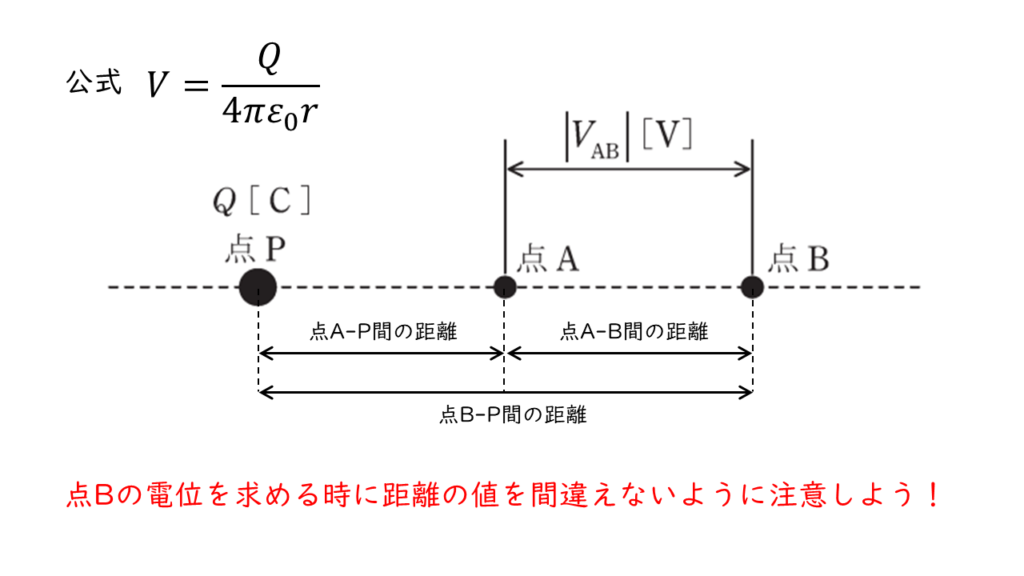
(a)の場合

点A，点Bにおける電位はそれぞれ以下のように計算できます。

$$ V_A = \frac{Q}{4 \pi ε_0 \times 2} = \frac{Q}{8\pi ε_0} $$

$$ V_B = \frac{Q}{4 \pi ε_0 \times (2+1)} = \frac{Q}{12\pi ε_0} $$

よって\(V_{AB}\ [V]\)の大きさは、

$$ \begin{align} V_{AB} &= V_A – V_B \\ &= \frac{Q}{8\pi ε_0}-\frac{Q}{12\pi ε_0} \\ &= \frac{3Q}{24\pi ε_0}-\frac{2Q}{24\pi ε_0} = \frac{Q}{24\pi ε_0} \end{align} $$

となります。同様に(b)～(d)の場合についても計算していきます。

(b)の場合

点A，点Bにおける電位はそれぞれ以下のように計算できます。

$$ V_A = \frac{Q}{4 \pi ε_0 \times 1} = \frac{Q}{4\pi ε_0} $$

$$ V_B = \frac{Q}{4 \pi ε_0 \times (1+2)} = \frac{Q}{12\pi ε_0} $$

よって\(V_{AB}\ [V]\)の大きさは、

$$ \begin{align} V_{AB} &= V_A – V_B \\ &= \frac{Q}{4\pi ε_0}-\frac{Q}{12\pi ε_0} \\ &= \frac{3Q}{12\pi ε_0}-\frac{Q}{12\pi ε_0} = \frac{Q}{12\pi ε_0} \end{align} $$

となります。

(c)の場合

点A，点Bにおける電位はそれぞれ以下のように計算できます。

$$ V_A = \frac{Q}{4 \pi ε_0 \times 0.5} = \frac{Q}{2\pi ε_0} $$

$$ V_B = \frac{Q}{4 \pi ε_0 \times (0.5+1)} = \frac{Q}{6\pi ε_0} $$

よって\(V_{AB}\ [V]\)の大きさは、

$$ \begin{align} V_{AB} &= V_A – V_B \\ &= \frac{Q}{2\pi ε_0}-\frac{Q}{6\pi ε_0} \\ &= \frac{3Q}{6\pi ε_0}-\frac{Q}{6\pi ε_0} = \frac{Q}{6\pi ε_0} \end{align} $$

となります。

(d)の場合

点A，点Bにおける電位はそれぞれ以下のように計算できます。

$$ V_A = \frac{Q}{4 \pi ε_0 \times 1} = \frac{Q}{4\pi ε_0} $$

$$ V_B = \frac{Q}{4 \pi ε_0 \times (1+0.5)} = \frac{Q}{6\pi ε_0} $$

よって\(V_{AB}\ [V]\)の大きさは、

$$ \begin{align} V_{AB} &= V_A – V_B \\ &= \frac{Q}{4\pi ε_0}-\frac{Q}{6\pi ε_0} \\ &= \frac{3Q}{12\pi ε_0}-\frac{2Q}{12\pi ε_0} = \frac{Q}{12\pi ε_0} \end{align} $$

となります。

以上の計算結果から，(a)のときが最小になり，(c)のときが最大となることが分かります。
よって答えは(2)になります。