問題
図のように,誘電体の種類,比誘電率,絶縁破壊電界,厚さがそれぞれ異なる三つの平行板コンデンサ①~③がある。極板の形状と大きさは同一で,コンデンサの端効果,初期電荷及び漏れ電流は無視できるものとする。上側の極板に電圧\(V_0\ [V]\)の直流電源を接続し,下側の極板を接地した。次の(a)及び(b)の問に答えよ。
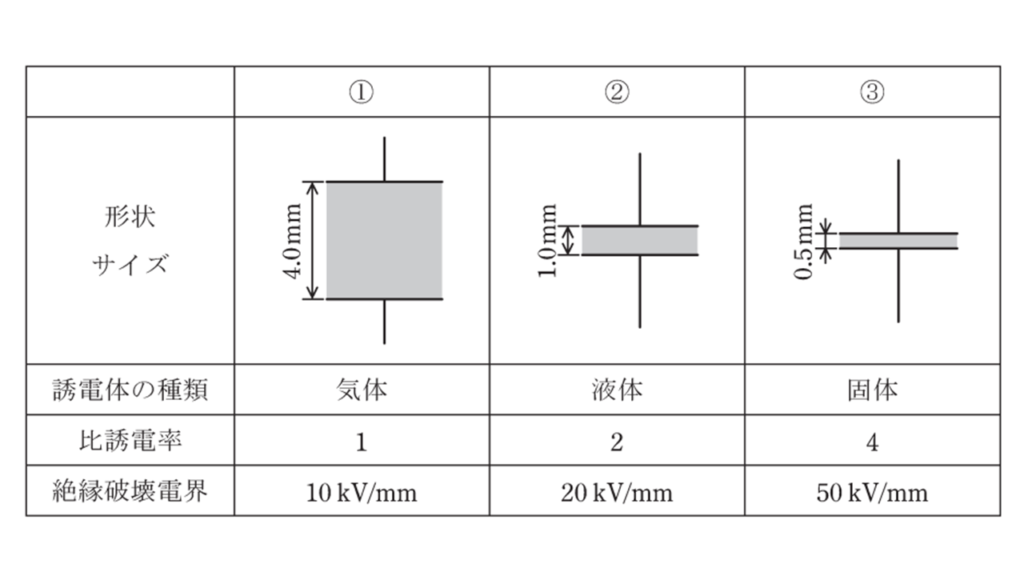
(a)
各平行板コンデンサの印加電圧の大きさが同一のとき,極板間の電界の強さの大きい順として,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{lc} \\ \hline (1) &①>②>③ \\ \hline (2) &①>③>② \\ \hline (3) &②>①>③ \\ \hline (4) &③>①>② \\ \hline (5) &③>②>① \\ \hline \end{array} $$
(b)
各平行板コンデンサへの印加電圧をそれぞれ徐々に上昇し,極板間の電界の強さが絶縁破壊電界に達したときの印加電圧(絶縁破壊電圧)の大きさの大きい順として,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{lc} \\ \hline (1) &①>②>③ \\ \hline (2) &①>③>② \\ \hline (3) &②>①>③ \\ \hline (4) &③>①>② \\ \hline (5) &③>②>① \\ \hline \end{array} $$
解説
答え:(a)-(5),(b)-(2)
(a) 各平行平板コンデンサの電界の強さを求める
3つの平行板コンデンサへの印加電圧が\(V_0\ [V]\)で等しいとき、極板間の電界の大きさは式\(V = E \times d \)から求めることができます。
$$ E_1 = \frac{V_0}{d_1} = \frac{V_0}{4.0 \times 10^{-3}} $$
$$ E_2 = \frac{V_0}{d_2} = \frac{V_0}{1.0 \times 10^{-3}} $$
$$ E_3 = \frac{V_0}{d_3} = \frac{V_0}{0.5 \times 10^{-3}} $$
以上の結果から、極板間の電界の大きさが大きい順に並べると③>②>①となり、答えは(5)になります。
比誘電率から考える場合
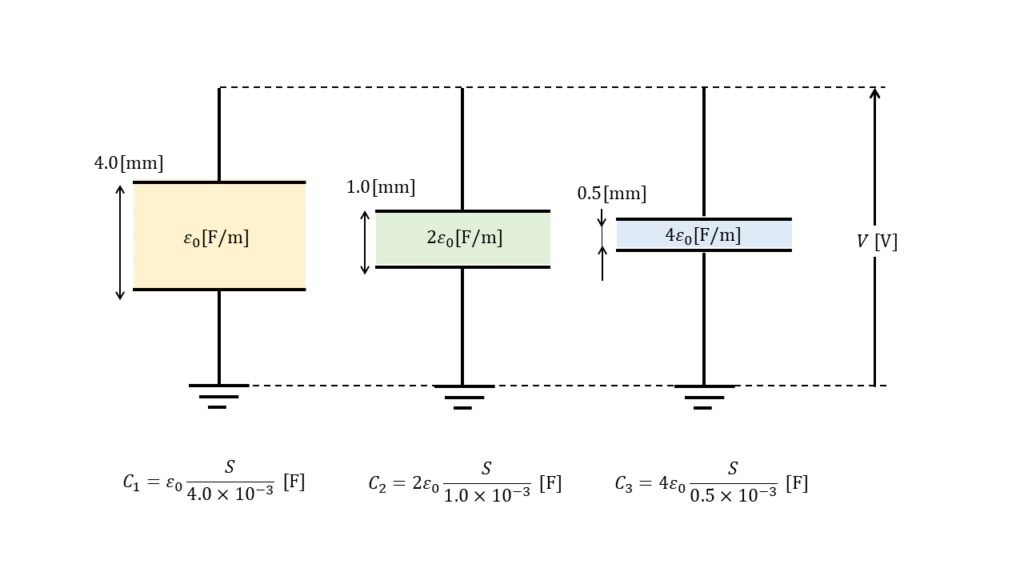
初めに、①,②,③の各コンデンサの静電容量\(C_1\ , \ C_2 \ , \ C_3\ [F]\)を求めます。問題文中に,極板の大きさと形状は全て同一と記載されているので,ここでは極板の面積を\(S\ [m^2]\)として考えることにします。また,真空中の誘電率を\(ε_0\ [F/m]\)とします。
$$ C_1 = ε_1ε_0 \times \frac{S}{d_1} =ε_0 \times \frac{S}{4.0 \times 10^{-3}} $$
$$ C_2 = ε_2ε_0 \times \frac{S}{d_2} =2ε_0 \times \frac{S}{1.0 \times 10^{-3}} $$
$$ C_3 = ε_3ε_0 \times \frac{S}{d_3} =4ε_0 \times \frac{S}{0.5 \times 10^{-3}} $$
次に各コンデンサに蓄えられる電気量\(Q\ [C]\)を計算します。
$$ Q_1 = C_1 \times V_0 = ε_0 \times \frac{S}{4.0 \times 10^{-3}} \times V_0 $$
$$ Q_2 = C_2 \times V_0 = 2ε_0 \times \frac{S}{1.0 \times 10^{-3}} \times V_0 $$
$$ Q_1 = C_1 \times V_0 = 4ε_0 \times \frac{S}{0.5 \times 10^{-3}} \times V_0 $$
極板から出る電束\(\psi \ [C] \)の大きさは電気量\(Q \ [C]\)と同じになるので,各コンデンサ内部の電束密度\(D_1\ , \ D_2 \ , \ D_3 \)は,以下のように計算できます。
$$ \begin{align} D_1 &= \frac{\psi _1}{S} = \frac{Q_1}{S} \\ &=ε_0 \times \frac{S}{4.0 \times 10^{-3}} \times V_0 \times \frac{1}{S} \\ &= \frac{ ε_0 V_0}{4.0 \times 10^{-3}} \end{align} $$
$$ \begin{align} D_2 &= \frac{\psi _2}{S} = \frac{Q_2}{S} \\ &=2ε_0 \times \frac{S}{1.0 \times 10^{-3}} \times V_0 \times \frac{1}{S} \\ &= \frac{ 2ε_0 V_0}{1.0 \times 10^{-3}} \end{align} $$
$$ \begin{align} D_3 &= \frac{\psi _3}{S} = \frac{Q_3}{S} \\ &=4ε_0 \times \frac{S}{0.5 \times 10^{-3}} \times V_0 \times \frac{1}{S} \\ &= \frac{ 4ε_0 V_0}{0.5 \times 10^{-3}} \end{align} $$
電界の大きさは式\(D = εE\)より
$$ \begin{align} E_1 &= \frac{D_1}{ε_1 ε_0} =\frac{\frac{ ε_0 V_0}{4.0 \times 10^{-3}}}{ε_0 } \\ &= \frac{V_0}{4.0 \times 10^{-3}} \end{align} $$
$$ \begin{align} E_2 &= \frac{D_2}{ε_2 ε_0} =\frac{\frac{ 2ε_0 V_0}{1.0 \times 10^{-3}}}{2ε_0 } \\ &= \frac{V_0}{1.0 \times 10^{-3}} \end{align} $$
$$ \begin{align} E_3 &= \frac{D_3}{ε_3 ε_0} =\frac{\frac{ 4ε_0 V_0}{0.5 \times 10^{-3}}}{4ε_0 } \\ &= \frac{V_0}{0.5 \times 10^{-3}} \end{align} $$
となります。\(V_0\ [V]\)の大きさは同じであるから,電界の大きさは\(E_3 >\ E_2 >\ E_1\)となります。よって答えは(5)になります。
別々のコンデンサの場合,電束密度が異なる点に注意しましょう。
(b) 各コンデンサの絶縁破壊電圧の大きさを求める
印加電圧\(V\ [V]\)を徐々に大きくしていった場合,表に記載されている絶縁破壊電界の大きさに到達するのは\(V\)がいくつの時か計算する問題です。
式\(E = \frac{V}{d}\)に絶縁破壊電界\(E\ [kV/mm]\)と極板間距離\(d\ [mm]\)を代入して計算することで絶縁破壊に到達する電圧\(V\)を求めることができます。
$$ V_{1max} = E_{1max} \times d_1 = 10 \times 4 = 40 \ [kV]$$
$$ V_{2max} = E_{2max} \times d_2 = 20 \times 1 = 20 \ [kV]$$
$$ V_{3max} = E_{3max} \times d_3 = 50 \times 0.5 = 25 \ [kV]$$
よって絶縁破壊電圧の大きさは①>③>②となり,答えは(2)になります。
ポイント
(b)問題で式\( V = E \times d\)を用いる必要があることから、(a)でもこの式を使えば計算できるよという誘導の様にも感じました。電験三種の中ではかなり優しい問題なので確実に得点しておきたいですね。
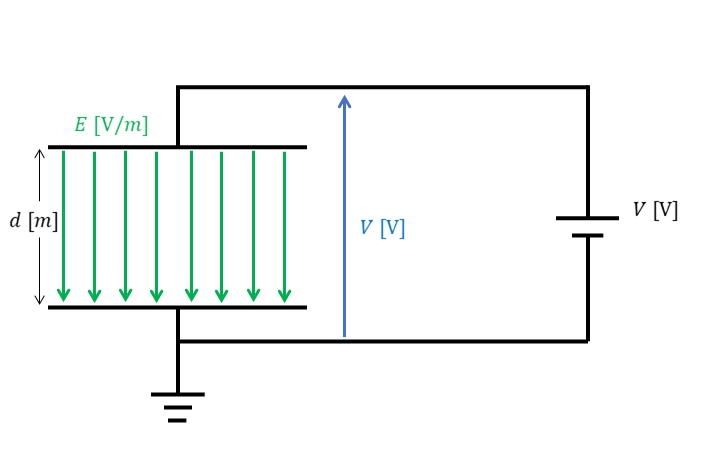
平行板コンデンサ内の電界の大きさ
平行板コンデンサの金属板上には、電荷が一様に分布しています。また、間にはさまれている誘電体(絶縁体)内部の電気力線密度も一様になり平等電界となります。
この時の電界の大きさは、以下のように表せます。$$ E = \frac{V}{d} $$
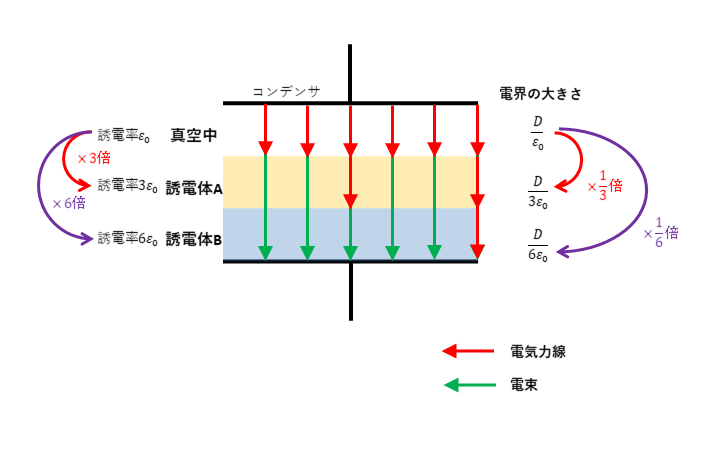
電束密度と電界の大きさ
電束の本数は、誘電率\(ε \ [F/m]\)を無視して考えるため電気力線の本数の\(ε\)倍になります。電気力線の密度は電界の大きさ\( E\ [V/m]\)を表すので、電束の密度(電束密度)\(D\ [C/m^2]\)は電界の大きさ\(E\)の\(ε\)倍になります。$$ D = ε \times E $$











コメント