問題
平等な磁束密度 \(B_0\ \rm[T]\) のもとで,一辺の長さが \(h\ \rm[m]\) の正方形ループ \(ABCD\) に直流電流 \(I\ \rm[A]\) が流れている。 \(B_0\) の向きは辺 \(AB\) と平行である。 \(B_0\) がループに及ぼす電磁力として,正しいものを次の(1)~(5)のうちから一つ選べ。

(1) 大きさ \(2IhB_0\ \rm[N]\) の力
(2) 大きさ \(4IhB_0\ \rm[N]\) の力
(3) 大きさ \(Ih^2B_0\ \rm[N⋅m]\) の偶力のモーメント
(4) 大きさ \(2Ih^2B_0\ \rm[N⋅m]\) の偶力のモーメント
(5) 力も偶力のモーメントも働かない
解説
答え:(4)
導体の各辺にはたらく力を考える
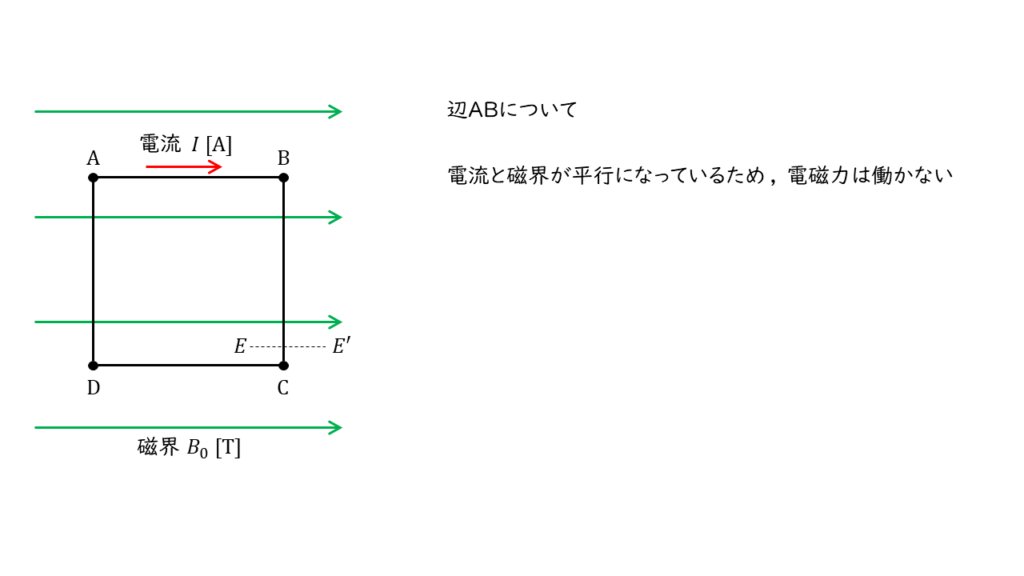
辺\(AB\)について
磁界と電流の向きが平行になっているため,電磁力が働きません。
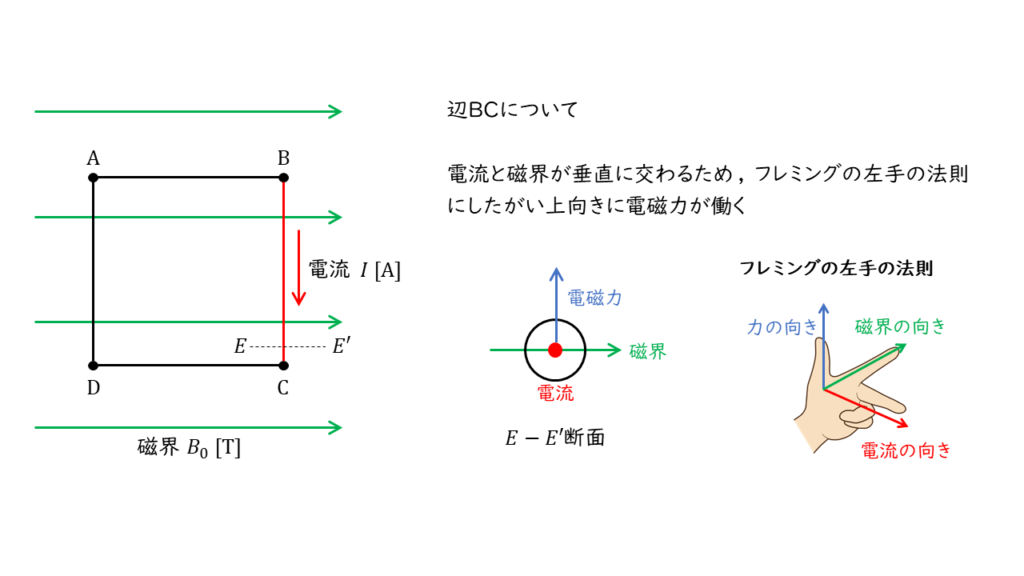
辺\(BC\)について
フレミングの左手の法則より,辺\(BC\)には上向きに力が働きます。
辺\(CD\)について
辺\(CD\)を流れる電流と磁界は,平行になるため,辺\(AB\)と同様に,電磁力が働きません。

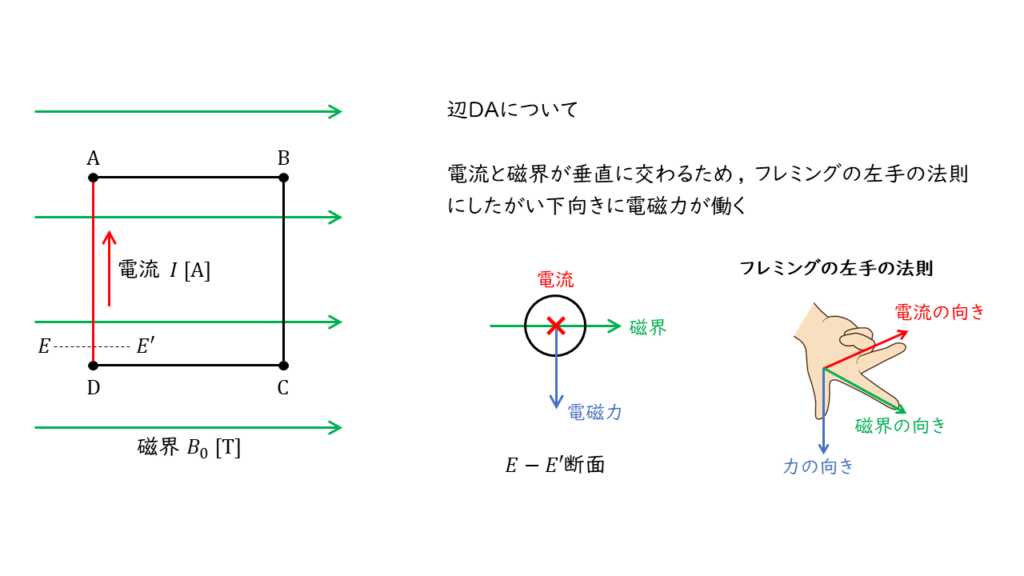
辺\(DA\)について
フレミングの左手の法則により,辺\(DA\)には,下向きの方向に電磁力が働きます。
ループ\(ABCD\)にはたらく力の種類と大きさを求める
以上のように,各辺にはたらく力をまとめて表すと下図のようになります。
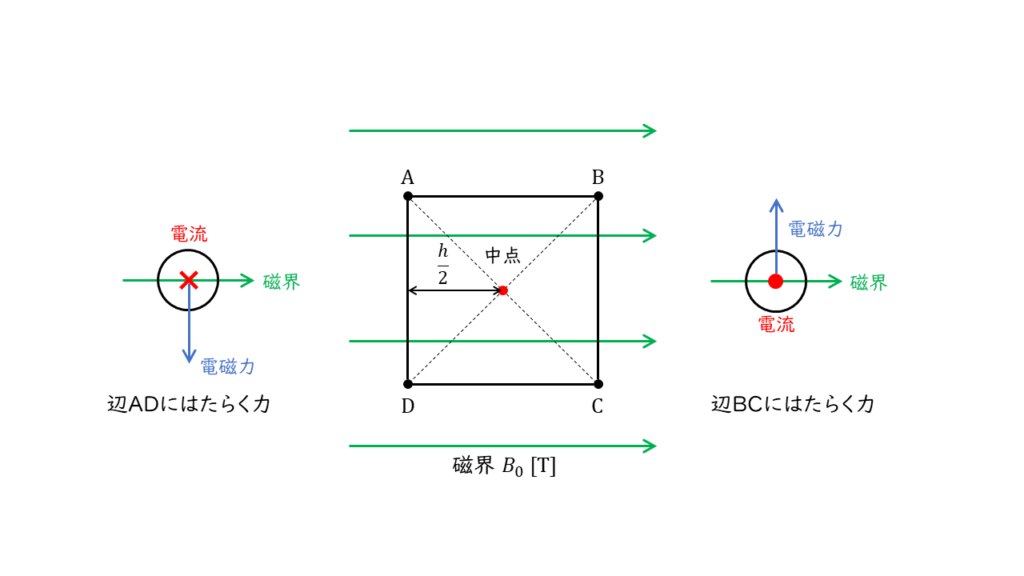
辺\(BC\)と辺\(DA\)は,平行な位置にあり,はたらく力は上下反対であるため,四角形の対角線が交わる点(中点)を中心とした回転するような力となります。

この時の回転力の大きさは,中点から辺\(BC\)および辺\(DA\)までの距離は, \(\displaystyle \frac{h}{2}\ \rm[m]\) であるから,問で与えられた条件を元に電磁力の大きさを計算すると,
\( \begin{align} 回転力 &= 1辺にはたらく電磁力 \times うでの長さ \times 2 \\ \\ T &= I \times B_0 \times h \times \displaystyle \frac{h}{2} \times 2 \\ \\ T &= Ih^2B_0 \ \rm[N・m] \end{align} \)
したがって,答えは(4)になります。











コメント