【過去問解説】R2理論　問5　抵抗値の大きさに関する選択問題

問題

次に示す， \(\rm A\) ， \(\rm B\) ， \(\rm C\) ， \(\rm D\) の四種類の電線がある。いずれの電線もその長さは \(1\ \rm km\) である。この四つの電線の直流抵抗値をそれぞれ \(R_A\ [\Omega]\) ， \(R_B\ [\Omega]\) ， \(R_C\ [\Omega]\) ， \(R_D\ [\Omega]\) とする。 \(R_A\) ～ \(R_D\) の大きさを比較したとき，その大きさの大きい順として，正しいものを次の(1)～(5)のうちから一つ選べ。ただし，\(\rho\) は各導体の抵抗率とし，また，各電線は等断面，等質であるとする。

\(\rm A\) ：断面積が \(9 \times 10^{-5} \ \rm m^2\) の鉄 \( \left( \rho = 8.90 \times 10^{-8}\ \rm \Omega \cdot m \right) \) でできた電線
\(\rm B\) ：断面積が \(5 \times 10^{-5} \ \rm m^2\) のアルミニウム \( \left( \rho = 2.50 \times 10^{-8} \ \rm \Omega \cdot m \right) \) でできた電線
\(\rm C\) ：断面積が \( 1 \times 10^{-5} \ \rm m^2\) の銀 \( \left( \rho = 1.47 \times 10^{-8} \ \rm \Omega \cdot m \right) \) でできた電線
\(\rm D\) ：断面積が \( 2 \times 10^{-5} \ \rm m^2\) の銅 \( \left( \rho = 1.55 \times 10^{-8} \ \rm \Omega \cdot m \right) \) でできた電線

(1)　 \( R_A ＞ R_C ＞ R_D ＞ R_B \)
(2)　 \( R_A ＞ R_D ＞ R_C ＞ R_B \)
(3)　 \( R_B＞ R_D ＞ R_C ＞ R_A \)
(4)　 \( R_C ＞ R_A ＞ R_D ＞ R_B \)
(5)　 \( R_D ＞ R_C ＞ R_A ＞ R_B \)

解説

答え：（4）

各抵抗の大きさを計算する

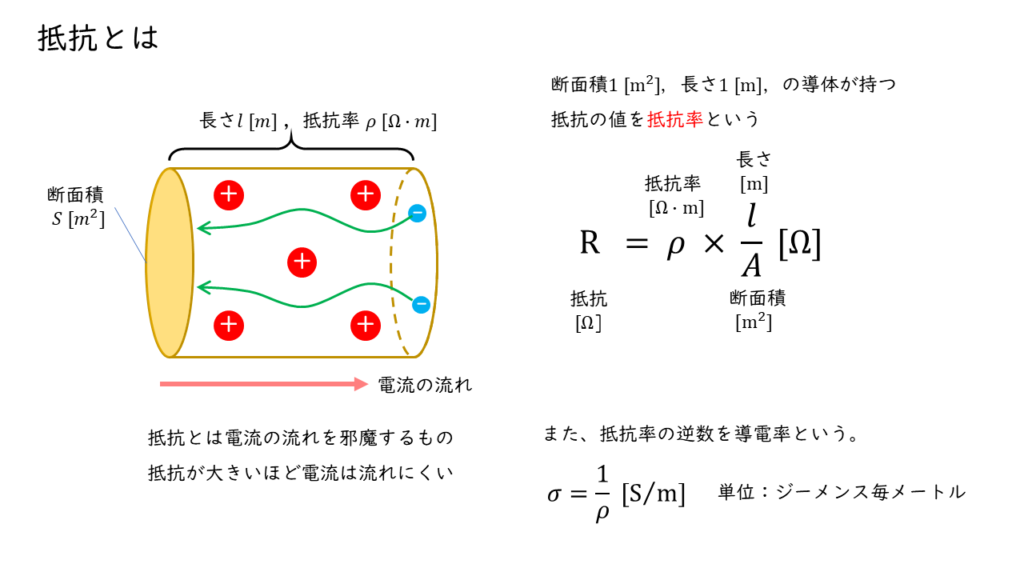
抵抗の大きさ \( R \ [\Omega]\) は，抵抗率を\(\rho \ \rm[\Omega \cdot m]\) ，断面積を \( A \ \rm [m^2]\) ，長さを \( l \ \rm [m]\) とすると，以下の式で表すことができます。

この式を使って，4種類の電線 \( \rm A ～ D\) の抵抗の大きさ \( R_A ～ R_D \ [\Omega]\) を計算します。

\(R_A\) の値を求める

電線の長さは \(1\ \rm km = 1,000 \ \rm m\) なので，電線\(\rm A\) の抵抗の大きさは，

\(\begin{align} R_A &= \rho \times \displaystyle \frac{l}{A} \\ \\ &= 8.90 \times 10^{-8} \times \displaystyle \frac{1000}{9 \times 10^{-5}} \\ \\ &= \displaystyle \frac{8.90 \times 10^{-5}}{9 \times 10^{-5}} \\ \\ &\approx 0.988 \Omega \end{align} \)

\(R_B\) の値を求める

電線\(\rm B\) の抵抗の大きさは，

\(\begin{align} R_B &= \rho \times \displaystyle \frac{l}{A} \\ \\ &= 2.50 \times 10^{-8} \times \displaystyle \frac{1000}{5 \times 10^{-5}} \\ \\ &= \displaystyle \frac{2.50 \times 10^{-5}}{5 \times 10^{-5}} \\ \\ &= 0.500 \Omega \end{align} \)

\(R_C\) の値を求める

電線\(\rm C\) の抵抗の大きさは，

\(\begin{align} R_C &= \rho \times \displaystyle \frac{l}{A} \\ \\ &= 1.47 \times 10^{-8} \times \displaystyle \frac{1000}{1 \times 10^{-5}} \\ \\ &= \displaystyle \frac{1.47 \times 10^{-5}}{1 \times 10^{-5}} \\ \\ &= 1.47 \Omega \end{align} \)

\(R_D\) の値を求める

電線\(\rm D\) の抵抗の大きさは，

\(\begin{align} R_D &= \rho \times \displaystyle \frac{l}{A} \\ \\ &= 1.55 \times 10^{-8} \times \displaystyle \frac{1000}{2 \times 10^{-5}} \\ \\ &= \displaystyle \frac{1.55 \times 10^{-5}}{2 \times 10^{-5}} \\ \\ &= 0.775 \Omega \end{align} \)

以上の結果から抵抗値の大きさを比較すると，

\( R_B > R_D > R_A > R_C\)

となるので，答えは(4)になります。