問題
直流の出力電流又は出力電圧が常に一定の値になるように制御された電源を直流安定化電源と呼ぶ。直流安定化電源の出力電流や出力電圧にはそれぞれ上限値があり,一定電流(定電流モード)又は一定電圧(定電圧モード)で制御されている際に負荷の変化によってどちらかの上限値を超えると,定電流モードと定電圧モードとの間で切り替わる。
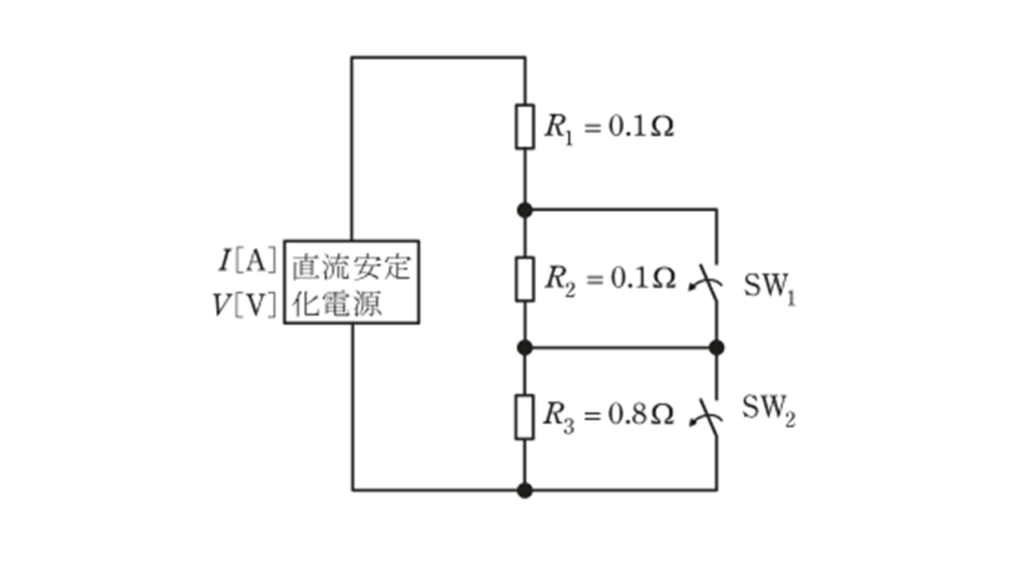
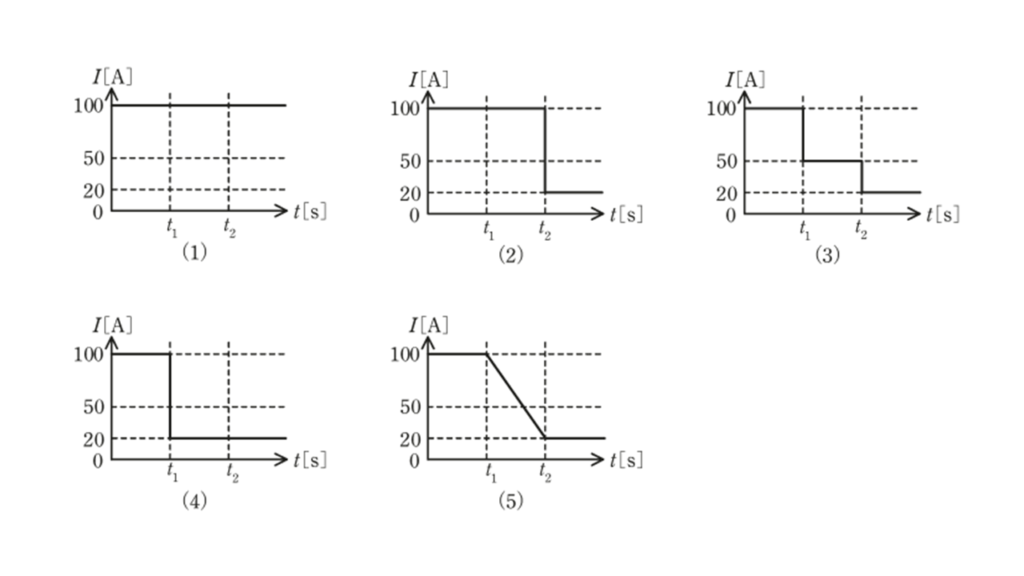
図のように,直流安定化電源(上限値: \(100\ \rm A\) , \(20\ \rm V\) ),三つの抵抗( \(R_1 = R_2 = 0.1\ \Omega\) ,\(R_3 = 0.8\ \Omega\) ),二つのスイッチ( \(\rm SW_1\) , \(\rm SW_2\) )で構成されている回路がある。両スイッチを閉じ,回路を流れる電流 \( I = 100\ \rm A\) の定電流モードを維持している状態において,時刻 \( t = t_1\ \rm[s]\) で \(\rm SW_1\) を開き,時刻 \( t = t_2\ \rm[s]\) で \(\rm SW_2\) を開くとき, \( I\ \rm[A]\) の波形として,正しいものを次の(1)~(5)のうちから一つ選べ。
解説
答え:(2)
時刻 \( t < t_1 \) の時,回路を流れる電流を求める
時刻が \(t_1 \ \rm [s]\) よりも小さいとき,スイッチ \(\rm SW_1\) ,\(\rm SW_2\) はともに閉じている状態にあるので,回路図は以下のように考えることができます。
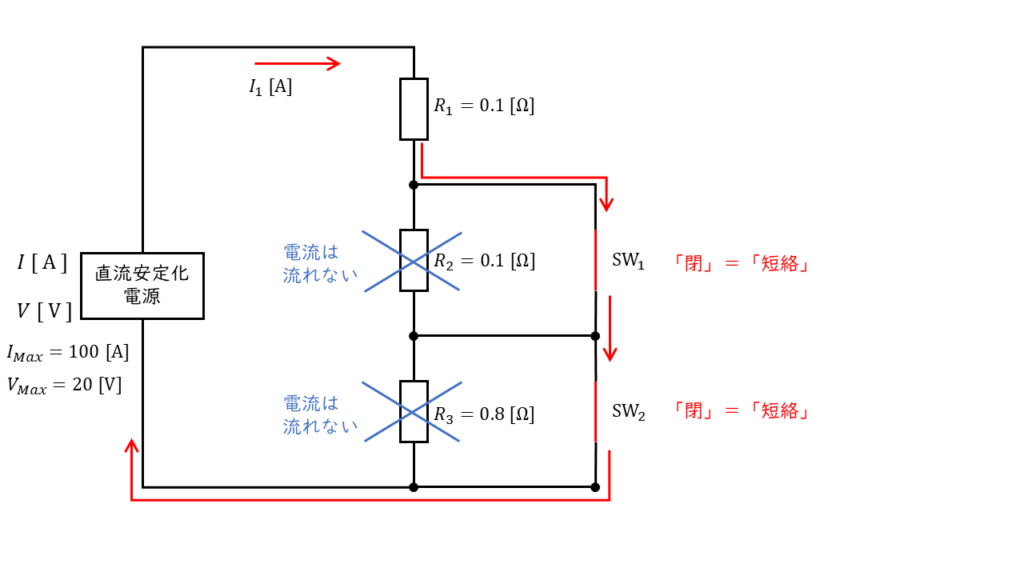
この時の回路を流れる電流 \(I_1\ \rm [A]\) の大きさは,オームの法則より,
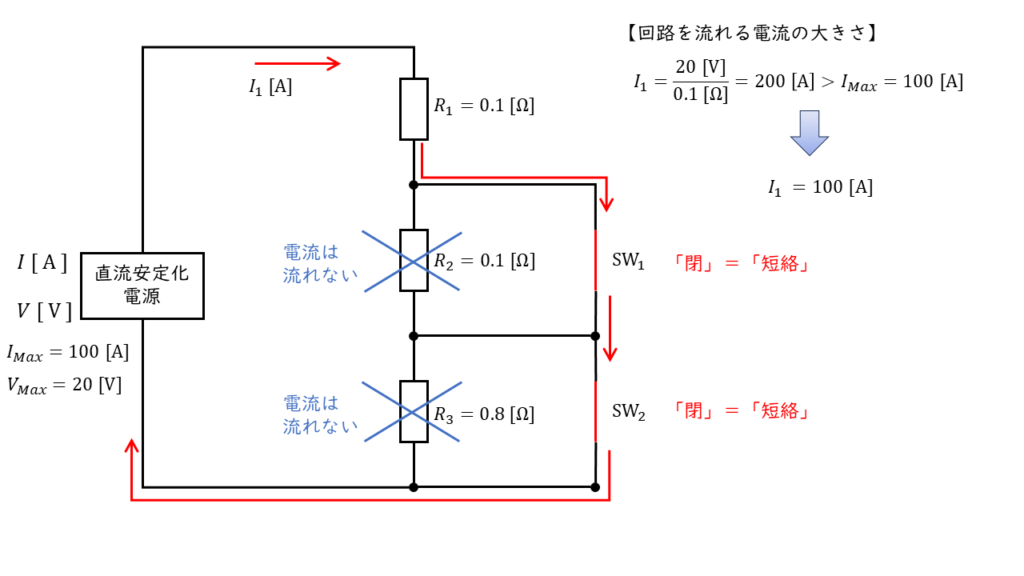
\(\begin{align} I_1 &= \displaystyle \frac{V}{R_1} \\ \\ &= \displaystyle \frac{20 \ \rm V}{0.1 \ \Omega} \\ \\ &= 200\ \rm [A] \end{align} \)
と計算できます。しかし,問いの条件より,安定化電源装置は最大で \(100\ \rm [A]\) までしか電流を出力することができないため,回路を流れる電流は, \(100 \ \rm [A]\) となります。
時刻 \( t_1 \leq t < t_2 \) の時,回路を流れる電流を求める
時刻が \( t = t_1\ \rm [s]\) となると,スイッチ \(SW_1\) が開放されるため,回路図は以下のようになります。
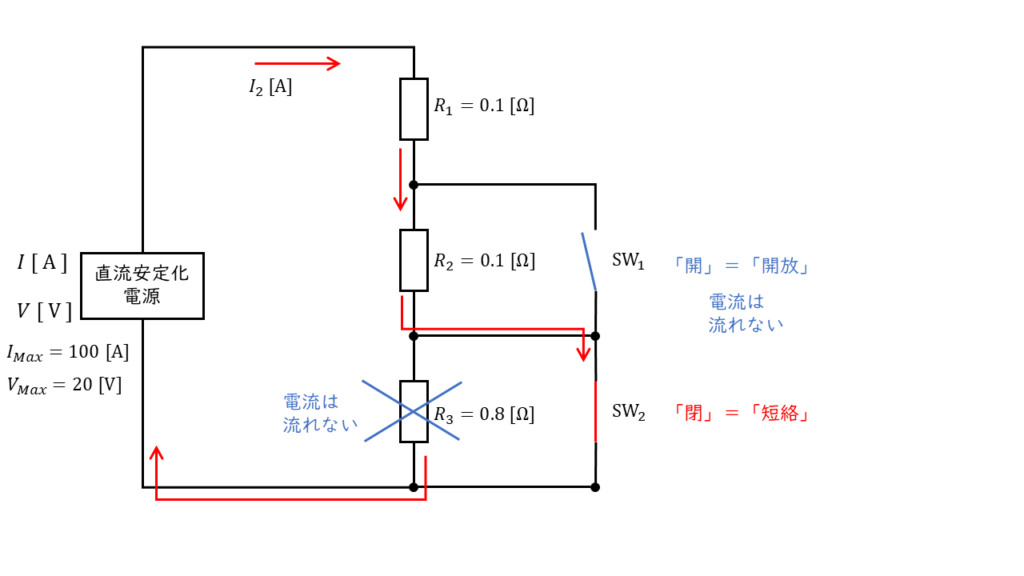
この時,回路を流れる電流 \(I_2\) の大きさは,オームの法則より,
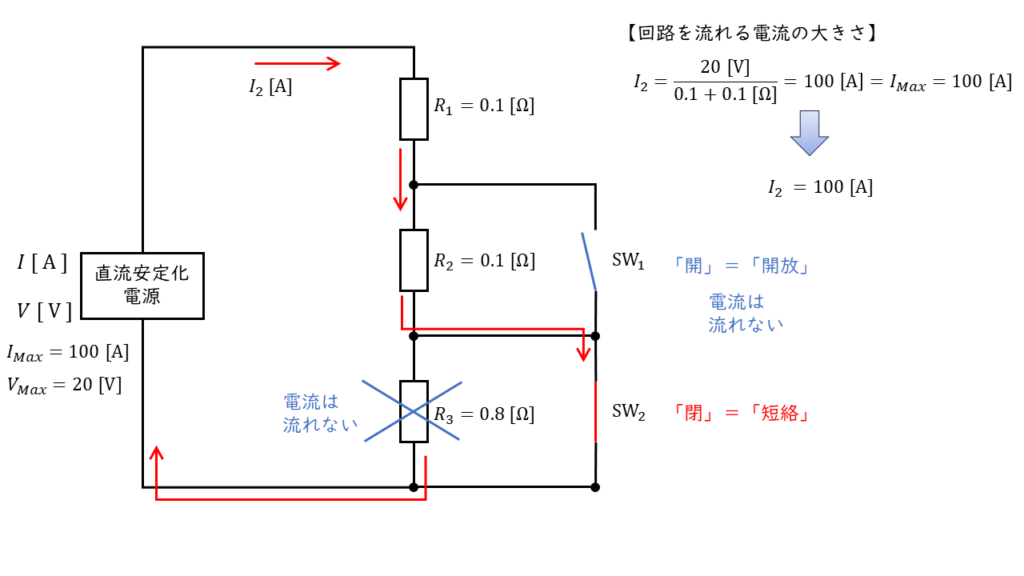
\(\begin{align} I_2 &= \displaystyle \frac{V}{R_1 + R_2} \\ \\ &= \displaystyle \frac{20 \ \rm V}{0.1 + 0.1 \ \Omega} \\ \\ &= 100 \ \rm [A] \end{align} \)
安定化電源装置の最大出力電流の大きさは,\(100 \ \rm [A]\) であるため,電流 \(I_2\) の大きさは,\(100 \ \rm [A]\) となります。
時刻 \( t_2 \leq t \) の時,回路を流れる電流を求める
時刻が,\(t_2\ \rm [s]\) になるとスイッチ \(\rm SW_2\) も解放されるため,回路図は以下のようになります。
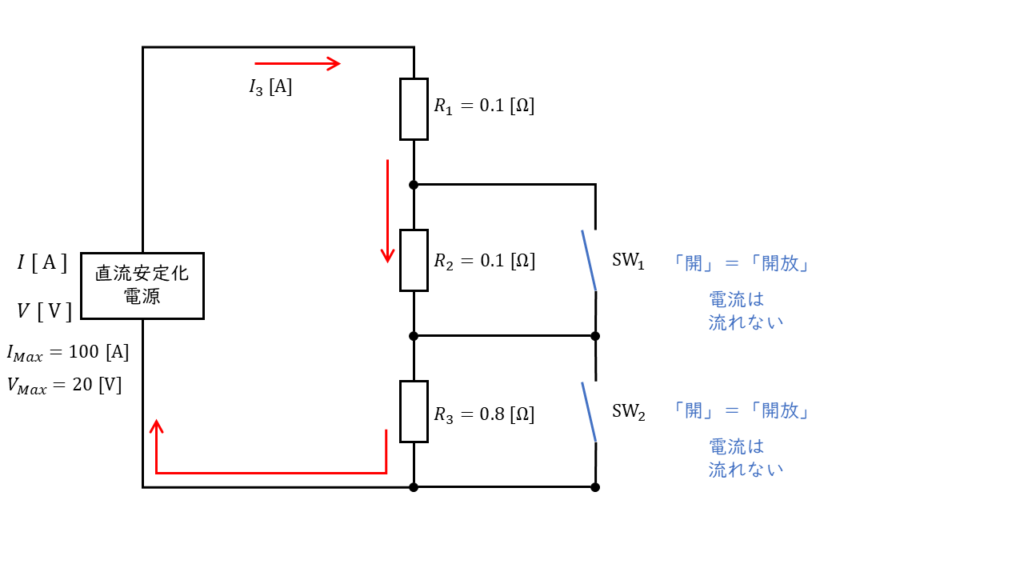
この時回路を流れる電流 \(I_3\) の大きさは,オームの法則より,
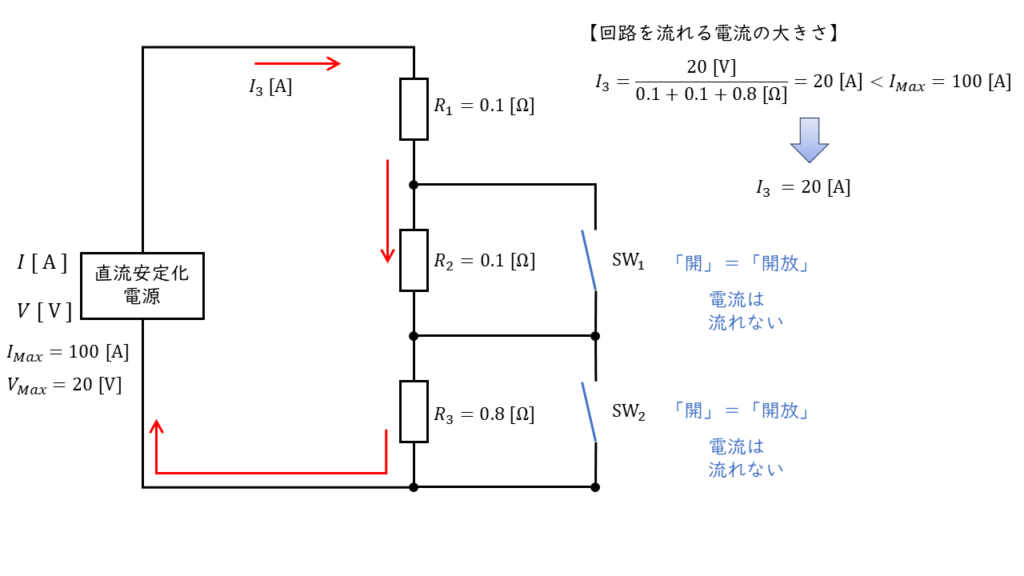
\(\begin{align} I_3 &= \displaystyle \frac{V}{R_1 + R_2 + R_3} \\ \\ &= \displaystyle \frac{20 \ \rm V}{0.1 + 0.1 + 0.8 \ \Omega} \\ \\ &= 20 \ \rm [A] \end{align} \)
電流 \(I_3\) の大きさは安定化電源装置の最大出力電流よりも小さい値のため,回路を流れる電流は計算結果の \(20\ \rm[A]\) が流れると判断できます。
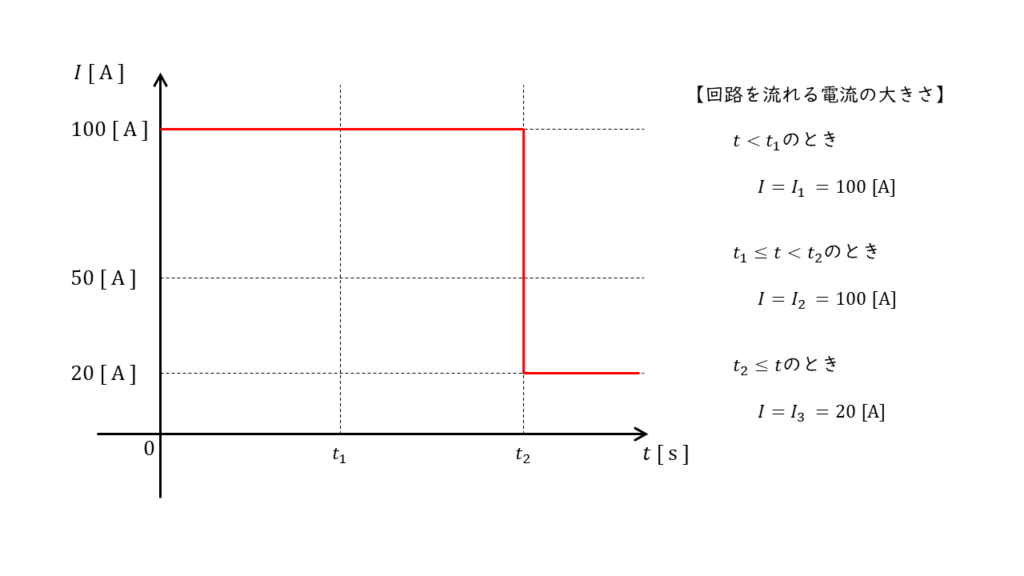
以上のことから時刻と電流の大きさをグラフに表すと下図のようになり,答えは(2)となることが分かります。











コメント