問題
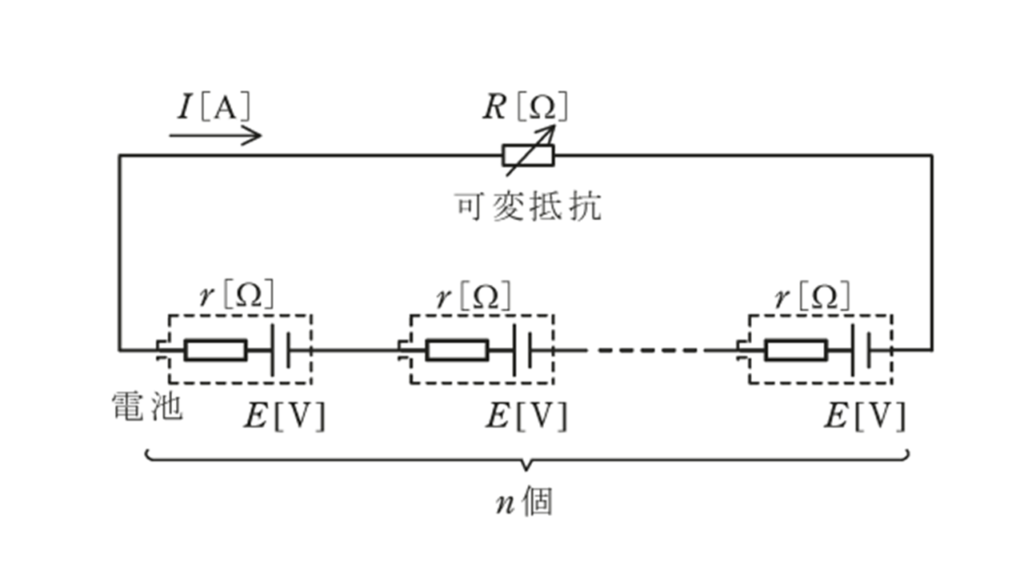
図のように,起電力 \(E\ \rm[V]\) ,内部抵抗 \(r\ \rm[\Omega]\) の電池 \(n\) 個と可変抵抗 \(R\ \rm[\Omega]\) を直列に接続した回路がある。この回路において,可変抵抗 \(R\ \rm[\Omega]\) で消費される電力が最大になるようにその値 \([\Omega]\) を調整した。このとき,回路に流れる電流 \(I\) の値 \(\rm[A]\) を表す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
(1) \(\displaystyle \frac{E}{r}\) (2) \(\displaystyle \frac{nE}{\left(\displaystyle \frac{1}{n}+n\right) r} \) (3) \(\displaystyle \frac{nE}{\left(1+n \right) r}\) (4) \(\displaystyle \frac{E}{2r}\) (5) \(\displaystyle \frac{nE}{2}\)
解説
答え:(4)
\(n = 1\) のときの電流の大きさを計算する
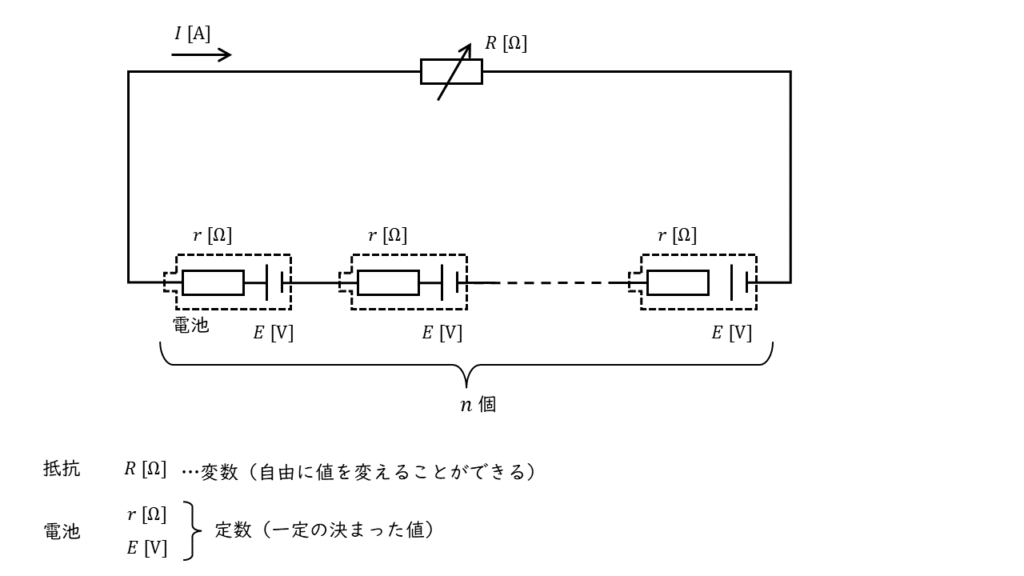
上図のように,電池が複数個ある問題では,\(n\) に1と2を代入した場合にどうなるかを考えると解答方法のパターンが導き出しやすいです。
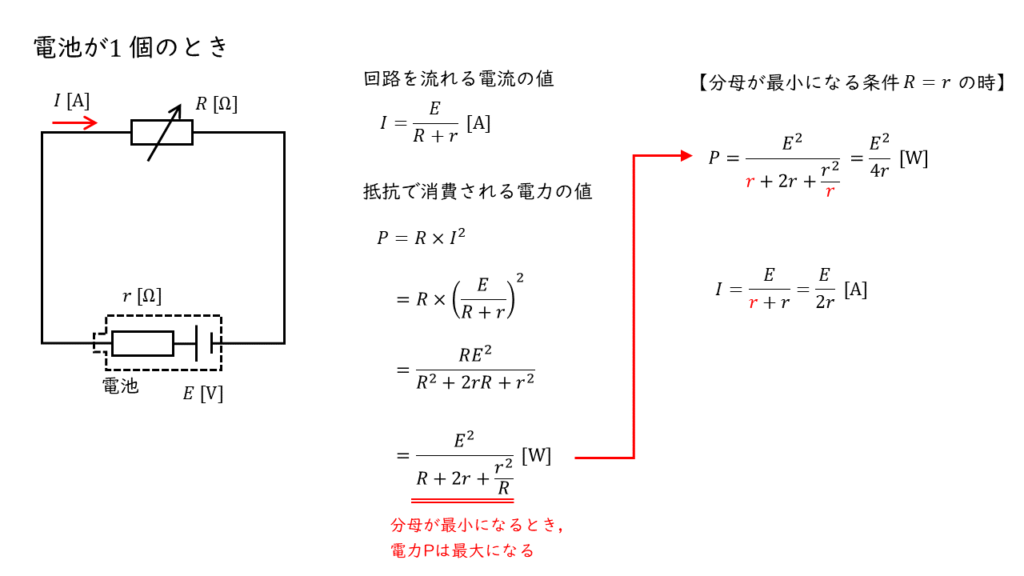
電池が1個の場合,回路図及び回路を流れる電流,可変抵抗 \(R\) で消費される電力は以下のように考えることができます。
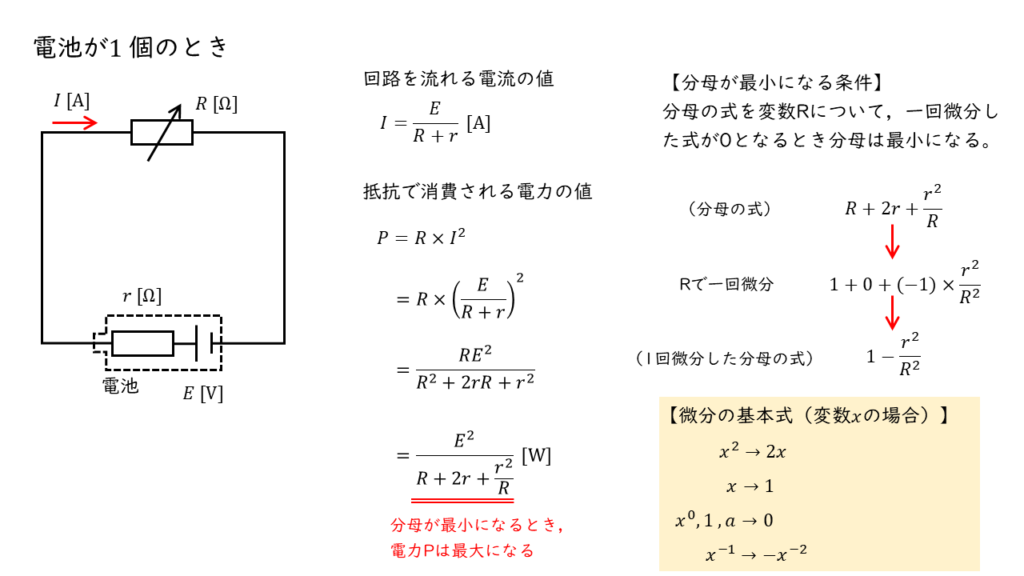
【回路を流れる電流】
\( I = \displaystyle \frac{E}{R + r} \ \rm [A]\)
【可変抵抗で消費する電力】
\(\begin{align} P &= R \times I^2 \\ \\ &= R \times \color{red}{ \left( \displaystyle \frac{E}{R + r} \right)^2 } \\ \\ &= \displaystyle \frac{RE}{R^2 + 2rR + r^2} \\ \\ &= \displaystyle \frac{E}{R + 2r + \displaystyle \frac{r^2}{R}} \ \rm [W] \end{align}\)
ここで,問題文の条件より,可変抵抗 \(R\ [\Omega]\) は常に消費電力が最大になるように調整されるので,電力の式を元に可変抵抗 \(R\) の値を考える必要があります。
電力が最大になるには,電力の式の分母が最小になればよいので,分母の部分を変数 \(R\) で1回微分し,微分で得られた式が \( =0\) となれば,最小になるといえます。
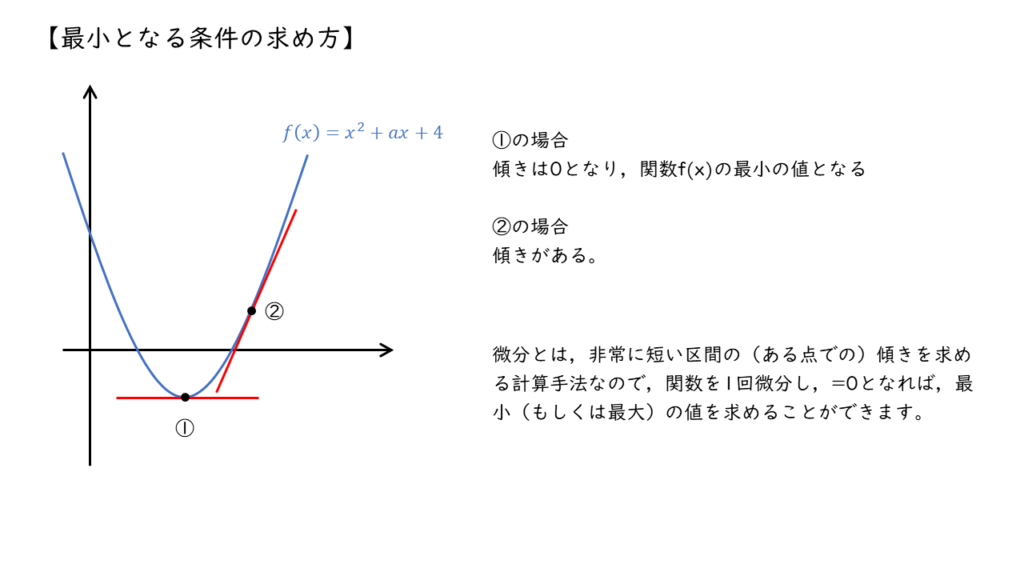
電力の式の分母を関数\(f \left(x \right) \)で表すすると,変数 \(R\) について1回微分した場合,
\( \begin{align} f \left(x \right) &= R + 2r + \displaystyle \frac{r^2}{R} \\ &\downarrow \\ f’ \left(x\right) &= 1 – \displaystyle \frac{r^2}{R^2} \end{align} \)
と表すことができます。微分した式が \(f’ \left(x \right) = 0\) となれば,元の式の最小の値がわかるので,
\(\begin{align} 1 – \displaystyle \frac{r^2}{R^2} &= 0 \\ \\ 1 &= \color{red}{\displaystyle \frac{r^2}{R^2}} \\ \\ R^2 &= r^2 \\ \\ R &= r \end{align} \)
以上が電力が最小となる可変抵抗 \(R\) の値になります。

この時,回路を流れる電流の大きさは,
【回路を流れる電流】
\(\begin{align} I &= \displaystyle \frac{E}{R + r} \\ \\ &= \displaystyle \frac{E}{\color{red}{r} + r} \\ \\ &= \displaystyle \frac{E}{2r} \ \rm[A] \end{align} \)
と求めることができます。
\( n = 2\) のときの電流の大きさを計算する
次に,\(n=2\) の場合について考えます。
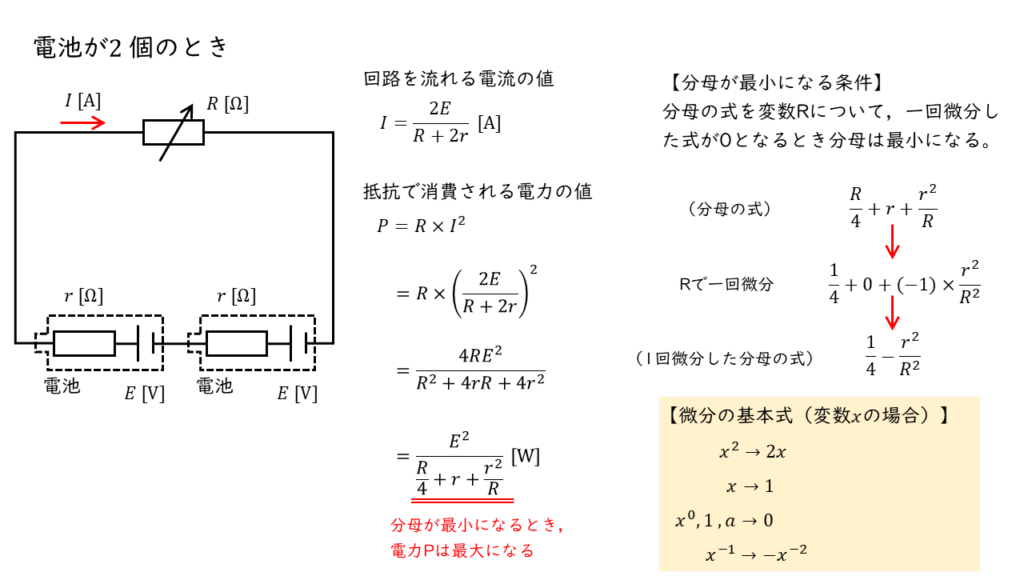
電池が2個に増えた場合,回路を流れる電流と可変抵抗で消費される電力はそれぞれ,以下の式で表すことができます。
【回路を流れる電流】
\( I = \displaystyle \frac{2E}{R + 2r} \ \rm [A]\)
【抵抗で消費される電力】
\(\begin{align} P &= RI^2 \\ \\ &= R \times \left( \displaystyle \frac{2E}{R + 2r} \right)^2 \\ \\ &= \displaystyle \frac{4RE^2}{R^2 + 4rR + 4r^2} \\ \\ &= \displaystyle \frac{E^2}{\displaystyle \frac{R}{4} + r + \displaystyle \frac{r^2}{R}} \ \rm[W] \end{align} \)
電池が1つの時と同様に,消費電力の式の分母を変数 \(R\) について微分することで,電力が最大となる条件を求めます。

電力の式の分母を関数\(f \left(x \right) \)で表すすると,変数 \(R\) について1回微分した場合,
\( \begin{align} f \left(x \right) &= \displaystyle \frac{R}{4} + r + \displaystyle \frac{r^2}{R} \\ &\downarrow \\ f’ \left(x\right) &= \displaystyle \frac{1}{4} – \displaystyle \frac{r^2}{R^2} \end{align} \)
と表すことができます。微分した式が \(f’ \left(x \right) = 0\) となれば,元の式の最小の値がわかるので,
\(\begin{align} \displaystyle \frac{1}{4} – \displaystyle \frac{r^2}{R^2} &= 0 \\ \\ \displaystyle \frac{1}{4} &= \color{red}{\displaystyle \frac{r^2}{R^2}} \\ \\ R^2 &= 4r^2 \\ \\ R &= 2r \end{align} \)
以上が電力が最小となる可変抵抗 \(R\) の値になります。この時,回路を流れる電流の大きさは,
【回路を流れる電流】
\(\begin{align} I &= \displaystyle \frac{2E}{R + 2r} \\ \\ &= \displaystyle \frac{2E}{\color{red}{2r} + 2r} \\ \\ &= \displaystyle \frac{E}{2r} \ \rm[A] \end{align} \)
と求めることができます。
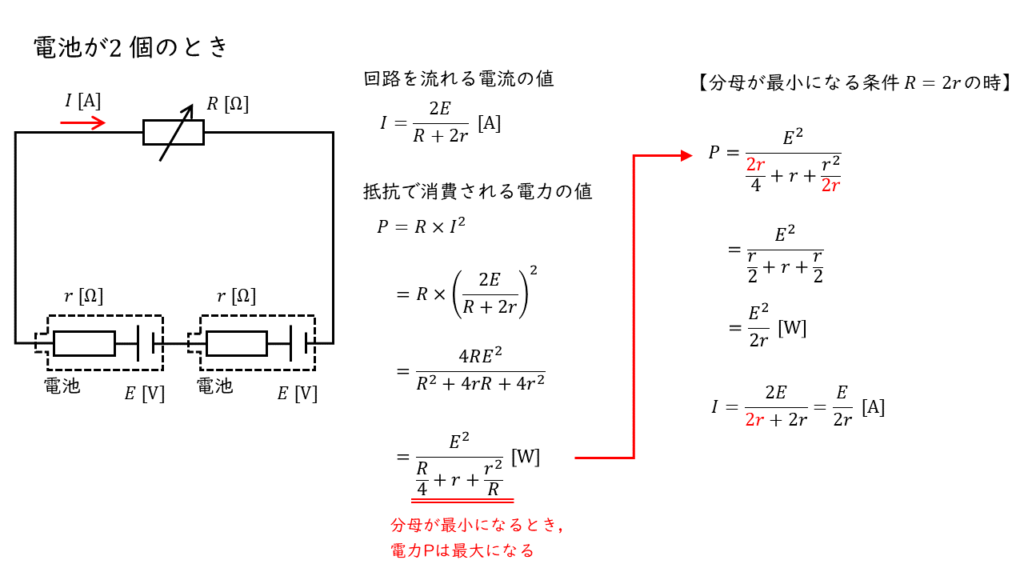
以上のことから,電池の数が変化しても問の条件においては,回路を流れる電流 \(I\) の値は,\(\displaystyle \frac{E}{2r}\) で一定となることが推測できます。
電池が \(n\) 個の場合について考える
最後に,電池の数が \(n\) 個の場合について考えます。

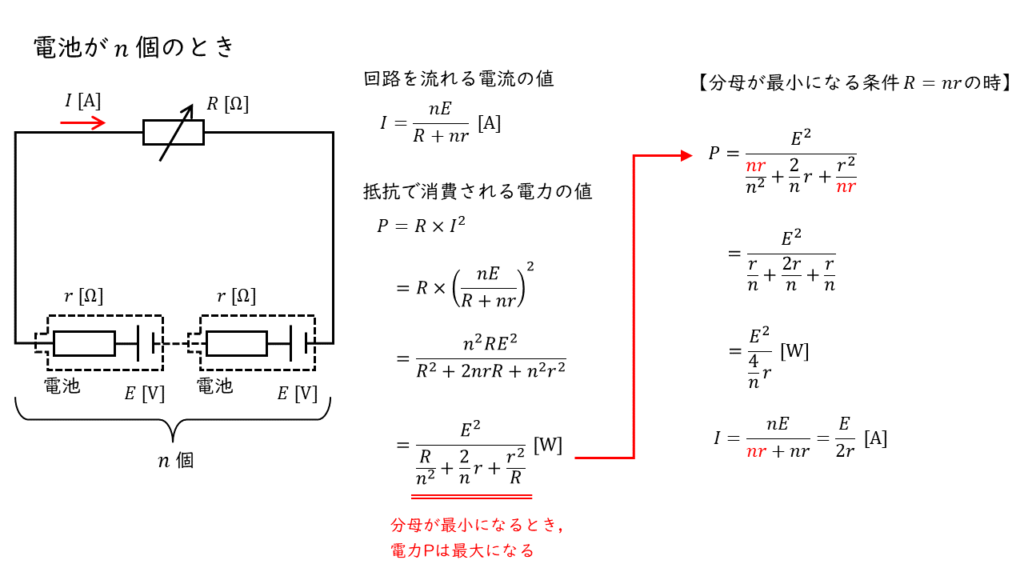
これまでと同様に計算でき,回路を流れる電流と可変抵抗で消費される電力の式は,
【回路を流れる電流】
\( I = \displaystyle \frac{nE}{R + nr} \ \rm [A] \)
【可変抵抗で消費される】
\( \begin{align} P &= R I^2 \\ \\ &= R \times \left( \displaystyle \frac{nE}{R + nr} \right)^2 \\ \\ &= \displaystyle \frac{n^2RE^2}{R^2 + 2nrR + n^2r^2} \\ \\ &= \displaystyle \frac{E^2}{\displaystyle \frac{R}{n^2} + \displaystyle \frac{2}{n}r + \displaystyle \frac{r^2}{R}} \ \rm[W] \end{align} \)
電力の式の分母を関数\(f \left(x \right) \)で表すすると,変数 \(R\) について1回微分した場合,
\( \begin{align} f \left(x \right) &= \displaystyle \frac{R}{n^2} + \displaystyle \frac{2}{n}r + \displaystyle \frac{r^2}{R} \\ &\downarrow \\ f’ \left(x\right) &= \displaystyle \frac{1}{n^2} – \displaystyle \frac{r^2}{R^2} \end{align} \)
と表すことができます。微分した式が \(f’ \left(x \right) = 0\) となれば,元の式の最小の値がわかるので,
\(\begin{align} \displaystyle \frac{1}{n^2} – \displaystyle \frac{r^2}{R^2} &= 0 \\ \\ \displaystyle \frac{1}{n^2} &= \color{red}{\displaystyle \frac{r^2}{R^2}} \\ \\ R^2 &= n^2 r^2 \\ \\ R &= nr \end{align} \)
以上が電力が最小となる可変抵抗 \(R\) の値になります。この時,回路を流れる電流の大きさは,
【回路を流れる電流】
\(\begin{align} I &= \displaystyle \frac{nE}{R + nr} \\ \\ &= \displaystyle \frac{nE}{\color{red}{nr} + nr} \\ \\ &= \displaystyle \frac{E}{2r} \ \rm[A] \end{align} \)
と求めることができます。
したがって,答えは(4)となります。











コメント