【過去問解説】　R4上期理論　問6　コンデンサを含む直流回路の計算問題

問題

図1に示すように，静電容量 \(C_1 = 4\ \mu \rm F\) と \(C_2 = 2\ \mu \rm F\) の二つのコンデンサが直列に接続され，直流電圧 \(6\ \rm V\) で充電されている。次に電荷が蓄積されたこの二つのコンデンサを直流電源から切り離し，電荷を保持したまま同じ極性の端子同士を図2に示すように並列に接続する。並列に接続後のコンデンサの端子間電圧の大きさ \(V\ \rm[V]\) の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

(1)　 \(\displaystyle \frac{2}{3}\) 　　(2)　 \(\displaystyle \frac{4}{3}\) 　　(3)　 \(\displaystyle \frac{8}{3}\) 　　(4)　 \(\displaystyle \frac{16}{3}\) 　　(5)　 \(\displaystyle \frac{32}{3}\)

解説

答え：（3）

図1の合成容量 \(C \ [\mu \rm F]\) と蓄えられる電荷量 \(q\ [\mu \rm C]\) を求める

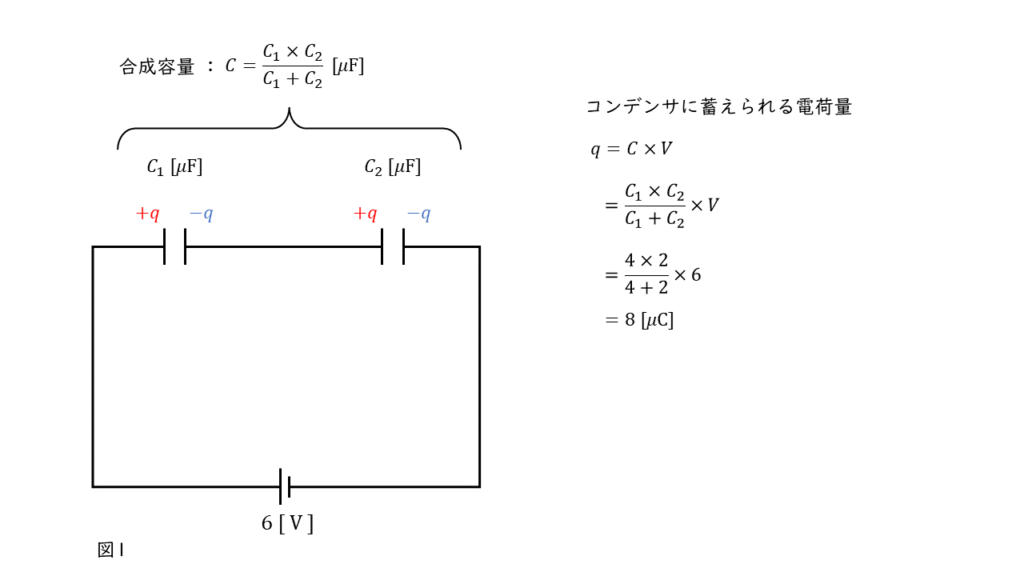
図1のように，コンデンサが直列に接続されているときの合成容量 \(C\) は，

\(\begin{align} C &= \displaystyle \frac{C_1 \times C_2}{C_1 + C_2} \\ \\ &= \displaystyle \frac{4 \times 2}{4 + 2} \\ \\ &= \displaystyle \frac{8}{6} = \displaystyle \frac{4}{3} \end{align} \)

となります。電源電圧の大きさが \(6\ \rm [V]\) であるから，蓄える電荷量 \(Q_1\) は，

\(\begin{align} q &= C \times V \\ \\ &= \displaystyle \frac{4}{3} \times 6 \\ \\ &= 8\ [\mu \rm C] \end{align} \)

図2の合成容量 \(C’ \ [\mu \rm F]\) と両端の電位差 \(V\ \rm [V]\) を求める

図2のように並列に接続した場合の合成容量 \(C’\) は，

\( C’ = C_1 + C_2 = 4 + 2 = 6\ [\mu \rm F]\)

となります。問の条件より，コンデンサには電荷は蓄えられたままであるから図2の回路は以下のようになっています。

したがって両端の電位差は，

\(\begin{align} V &= \displaystyle \frac{2 \times q}{C’} \\ \\ &= \displaystyle \frac{2 \times 8 \mu \rm F}{6 \mu \rm F} \\ \\ &=\displaystyle \frac{8}{3} \end{align} \)

となり，答えは(3)になります。