問題
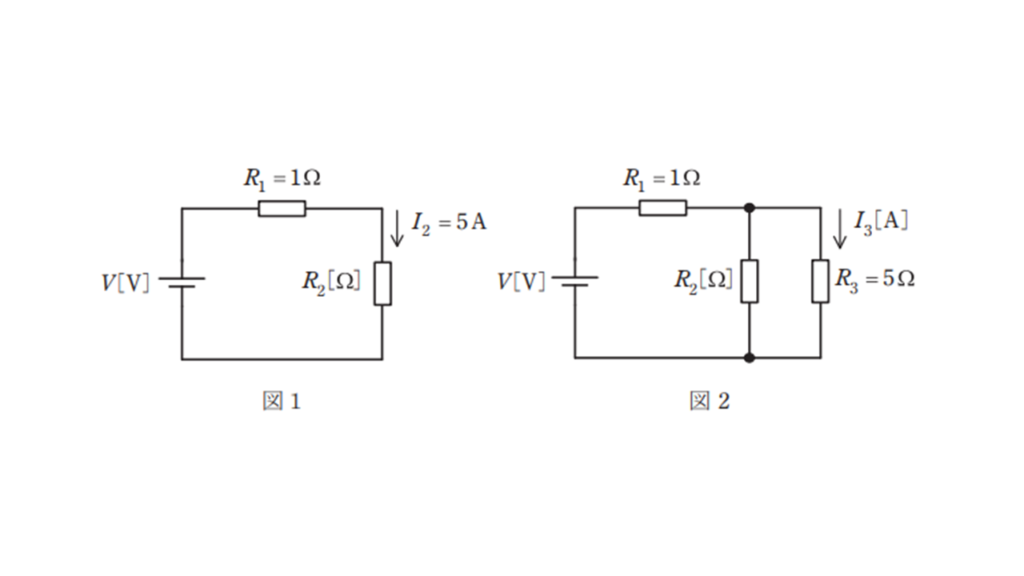
図1のように,二つの抵抗 \(R_1 = 1\ \Omega\) , \(R_2\ [\Omega]\) と電圧 \(V\ \rm[V]\) の直流電源からなる回路がある。この回路において,抵抗 \(R_2\ [\Omega]\) の両端の電圧値が \(100\ \rm V\) ,流れる電流 \(I_2\) の値が \(5\ \rm A\) であった。この回路に図2のように抵抗 \(R_3 = 5\ \Omega\) を接続したとき,抵抗 \(R_3\ [\Omega]\) に流れる電流 \(I_3\) の値 [A] として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(4.2\) (2) \(16.8\) (3) \(20\) (4) \(21\) (5) \(26.3\)
解説
答え:(2)
図1より 抵抗 \(R_2\) と 電源電圧 \(V\) の大きさを求める

問の条件より,図1の回路を流れる電流は \(I_2 = 5\ \rm A\) ,抵抗 \(R_2\) の両端にかかる電圧の大きさは \(100\ \rm V\) であるから,オームの法則より,
\( R_2 = \displaystyle \frac{100\ \rm V}{5\ \rm A} = 20 \Omega \)
と求めることができます。
また,抵抗 \(R_1\) の両端にかかる電圧の大きさ \(V_1\) は,
\( V_1 = 5 \ \rm A \times 1 \ \Omega = 5 \ \rm V\)
と計算できるので,電源電圧 \(V\) の大きさは,
\( V = V_1 + V_2 = 5 + 100 = 105\ \rm V\)
となります。
図2の回路を計算する
初めに,図2の回路における並列部分の合成抵抗の大きさを求めます。
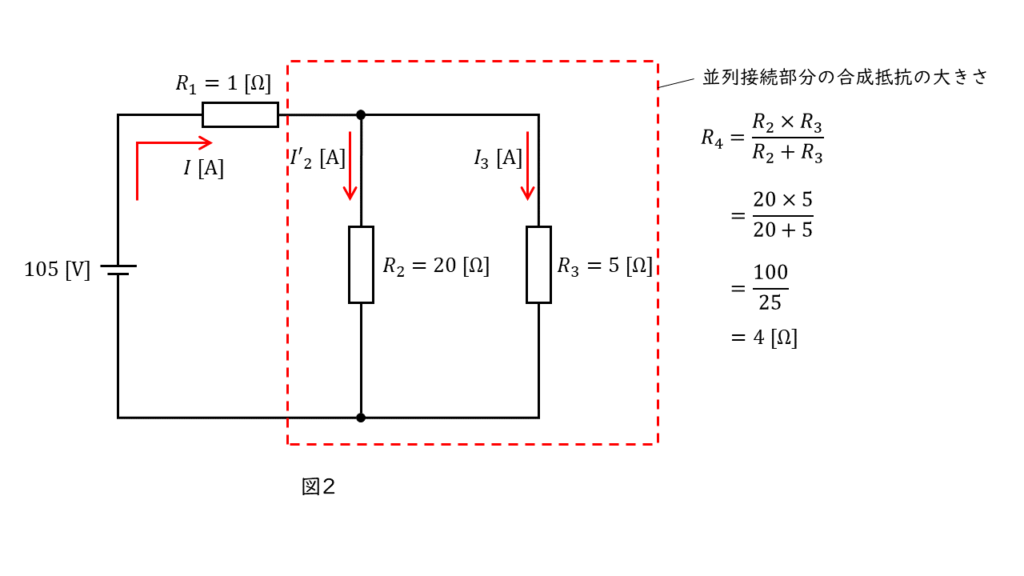
合成抵抗 \(R_4\) の大きさは,
\(\begin{align} R_4 &= \displaystyle \frac{R_2 \times R_3}{R_2 + R_3} \\ \\ &= \displaystyle \frac{20 \times 5}{20 + 5} \\ \\ &= \displaystyle \frac{100}{25} \\ \\ &= 4 \ \Omega \end{align} \)
次に,回路全体を流れる電流の大きさを求めます
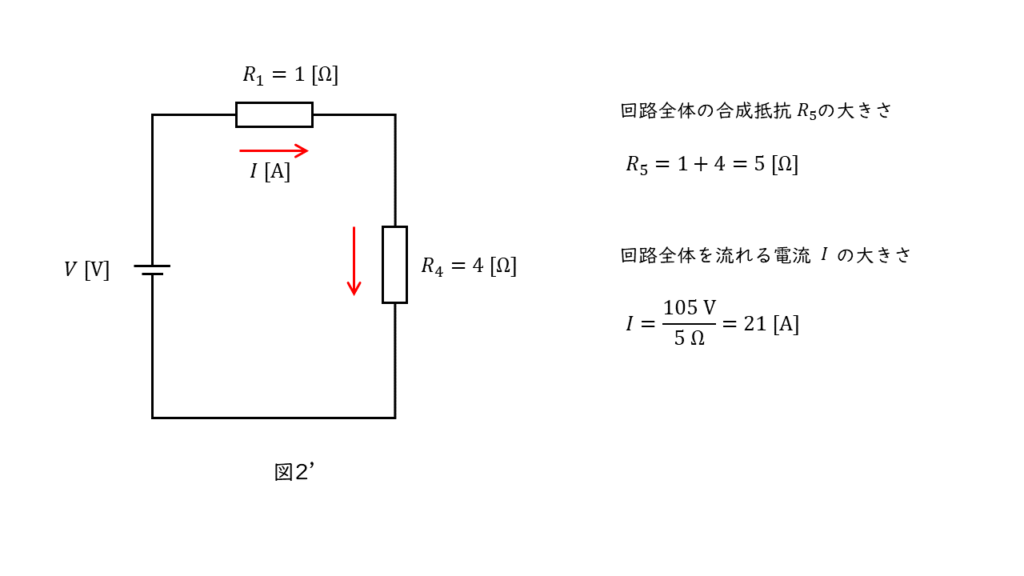
直列に接続された抵抗の合成抵抗の大きさは,各抵抗の大きさの和で求められるので,
\( R_5 = R_1 + R_4 = 1 + 4 = 5\)
となり,電源電圧 \(V = 105 \ rm V\) と合成抵抗の大きさから,回路を流れる電流は,
\( I = \displaystyle \frac{105}{5} = 21 \ \rm A\)
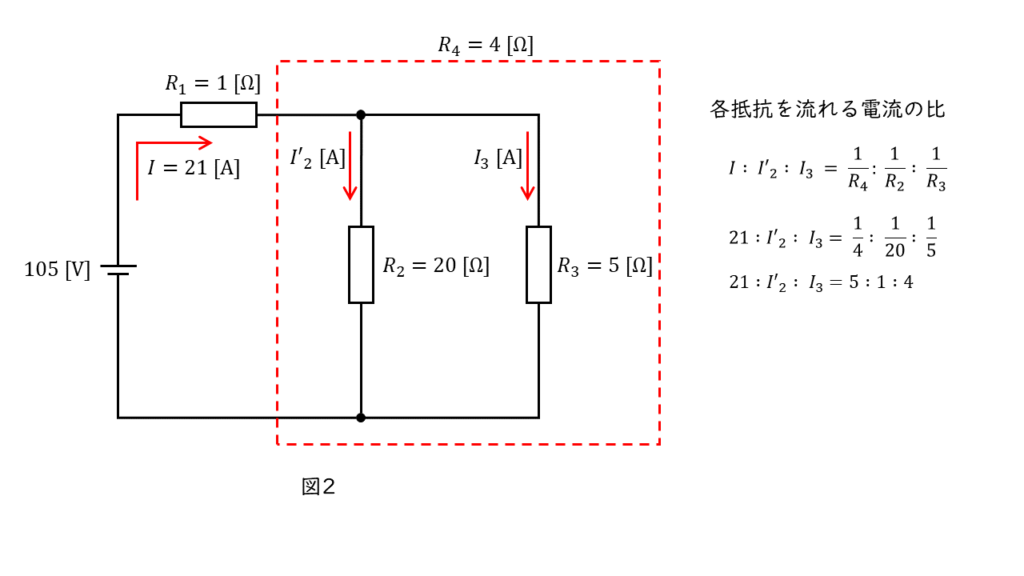
並列部分の抵抗\(R_2\) ,\(R_3\) に流れ込む電流をそれぞれ,\(I_2\) ,\(I_3\) とすると,
\( I = I_2 + I_3 \)
と表すことができます。
並列部分に流れる込む電流の大きさは,抵抗の大きさの逆数に比例するので,
\(\begin{align} I : I_2 : I_3 &= \displaystyle \frac{1}{R_4} : \displaystyle \frac{1}{R_2} : \displaystyle \frac{1}{R_3} \\ \\ 21 : I_2 : I_3 &= \displaystyle \frac{1}{4} : \displaystyle \frac{1}{20} : \displaystyle \frac{1}{5} \\ \\ 21 : I_2 : I_3 &= 5 : 1 : 4 \end{align} \)
したがって,抵抗 \(R_3\) に流れ込む電流 \(I_3\) の大きさは,
\( I_3 = 21 \times \displaystyle \frac{4}{5} = 16.8 \ \rm A\)
となり,答えは(2)となります。











コメント