【過去問解説】R4上期理論　問7　抵抗のみの直流回路の計算問題

問題

図のように，抵抗  \(6\) 個を接続した回路がある。この回路において， \(\rm ab\) 端子間の合成抵抗の値が \(0.6\ \Omega\) であった。このとき，抵抗 \(R_x\) の値 \([\Omega]\) として，最も近いものを次の(1)～(5)のうちから一つ選べ。

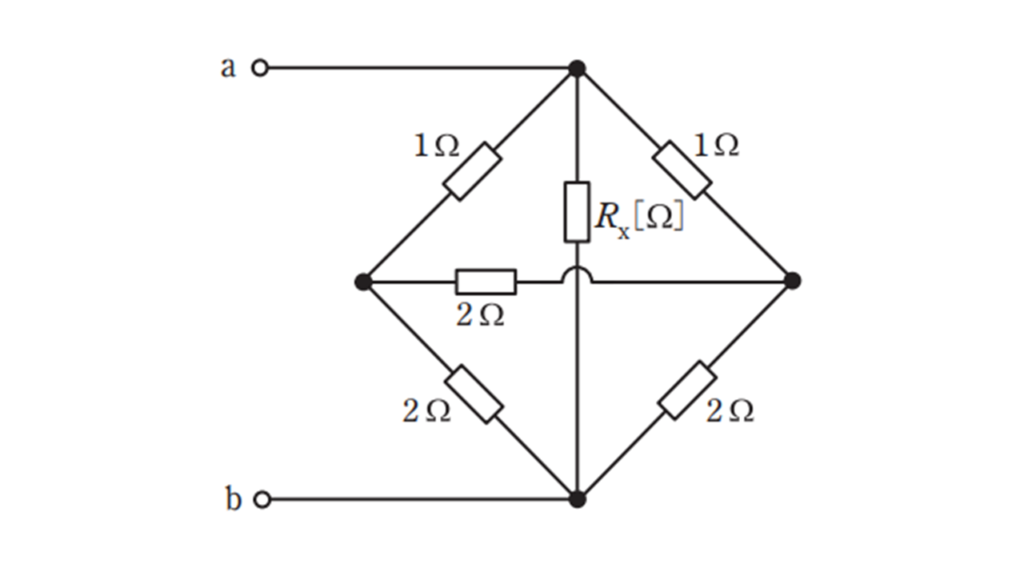
(1)　 \(1.0\)  　　(2)　 \(1.2\)  　　(3)　 \(1.5\)  　　(4)　 \(1.8\)  　　(5)　 \(2.0\)

解説

答え：（1）

問いの回路図を変形する

問いの回路図のままでは複雑で扱いにくいため，回路図を変形していきます。

まず，抵抗値が未知の抵抗 \(R_x\) はブリッジ回路と並列に接続しているとみなせるので，下図のように回路を変形します。

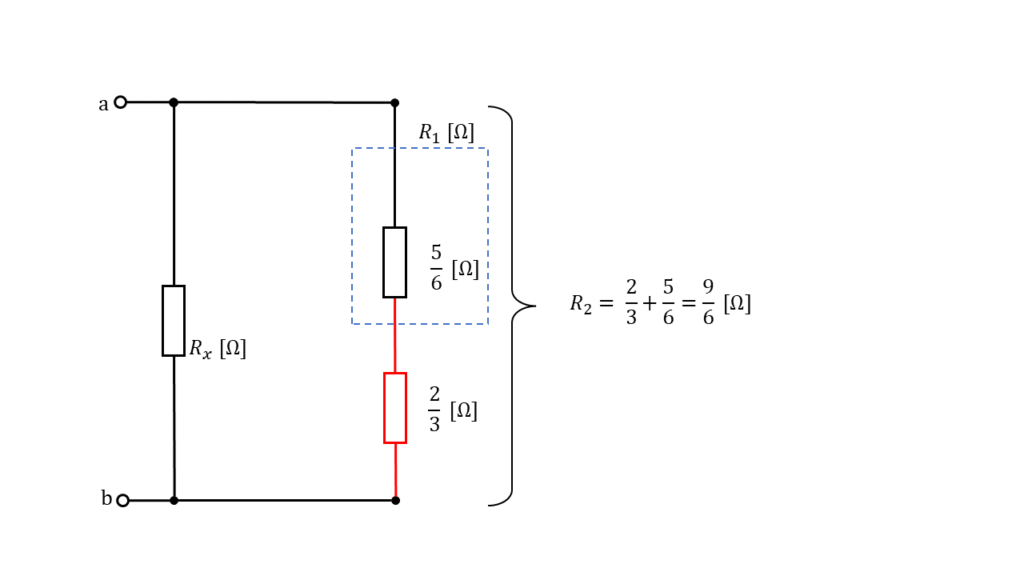
\(2\ [\Omega]\) の抵抗の結線を \(\Delta\) からYに変形する

 上図の赤色の部分は \(\Delta\) 結線であるため，回路を考えやすくするために，Y結線に変換します。

\(\Delta\) 結線部分の全ての抵抗値が \(2\ [\Omega]\) で同じであるため，Y結線に返還後の抵抗値は，元の抵抗値の \(\displaystyle \frac{1}{3}\) となるので，\(\displaystyle \frac{2}{3}\) と表すことができます。

合成抵抗の値を計算する

上図の右側の並列部分の合成抵抗 \(R_1\) は，

\(\begin{align} \displaystyle \frac{1}{R_1} &= \displaystyle \frac{1}{\displaystyle \frac{3+2}{3}} + \displaystyle \frac{1}{\displaystyle \frac{3+2}{3}} \\ \\ &= \displaystyle \frac{3}{5} + \displaystyle \frac{3}{5} \\ \\ \displaystyle \frac{1}{R_1} &= \displaystyle \frac{6}{5} \\ \\ R_1 &= \displaystyle \frac{5}{6} \end{align} \)

と計算することができます。

よって右側部分全体の合成抵抗 \(R_2\) は，

\(\begin{align} R_2 &= \displaystyle \frac{5}{6} + \displaystyle \frac{2}{3} \\ \\ &= \displaystyle \frac{5 \color{red}{ + 4}}{6} \\ \\ &= \displaystyle \frac{9}{6} \\ \\ &= \displaystyle \frac{3}{2} \\ \\ R_2 &= 1.5 \ [\Omega] \end{align} \)

次に，回路全体の合成抵抗の値 \(\displaystyle \frac{6}{10} \ [\Omega]\) から，抵抗 \(R_x\) の値を計算します。

\(\begin{align} \displaystyle \frac{10}{6} &= \displaystyle \frac{1}{R_x} + \displaystyle \frac{1}{R_2} \\ \\ &= \displaystyle \frac{1}{R_x} + \displaystyle \frac{1}{\displaystyle \frac{3}{2}} \\ \\ \displaystyle \frac{10}{6} &= \displaystyle \frac{1}{R_x} + \displaystyle \frac{2}{3} \\ \\ \displaystyle \frac{10}{6} \color{red}{ – \displaystyle \frac{2}{3}} &= \displaystyle \frac{1}{R_x} \\ \\ \displaystyle \frac{1}{R_x} &= \displaystyle \frac{10}{6} – \displaystyle \frac{4}{6} \\ \\ &= \displaystyle \frac{6}{6} \\ \\ R_x &= \displaystyle \frac{6}{6} = 1.0 \end{align} \)

となり，抵抗 \(R_x\) の値は \(1\) と求めることができます。

別解

抵抗値が未知の抵抗 \(R_x\) はブリッジ回路と並列に接続しているとみなせるので，下図のように回路を変形します。

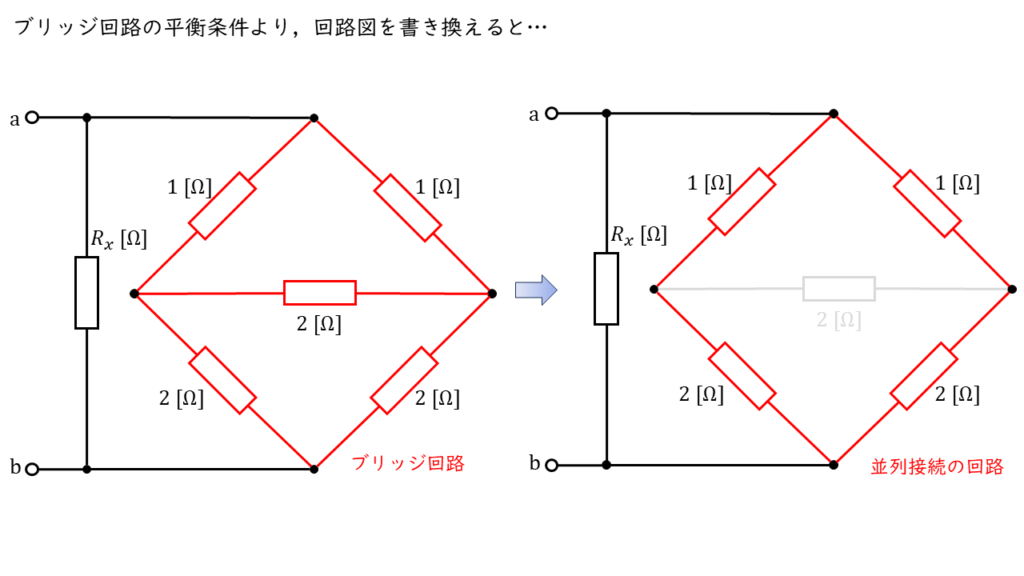
この時，ブリッジ回路の部分は，ブリッジ回路の平衡条件を満たしているので，っ中央の \(2\ \Omega\) の抵抗には電流が流れないため，以下のように回路を書き替えることもできます。

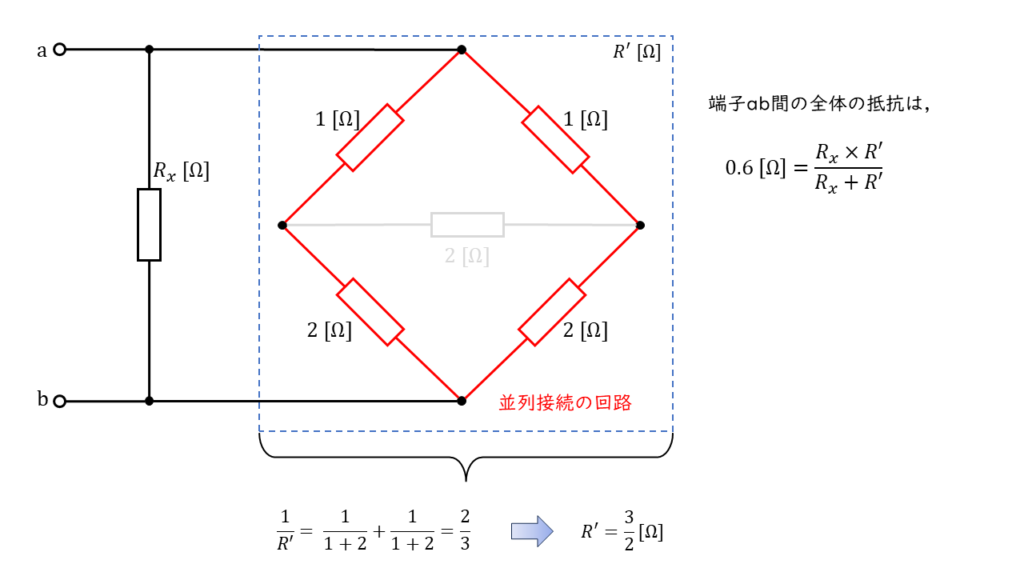
ブリッジ回路部分は，単なる抵抗の並列接続の回路とみなすことができるようになりました。並列回路部分の合成抵抗 \(R’\) は，

\(\begin{align} \displaystyle \frac{1}{R’} &= \displaystyle \frac{1}{1+2} +\displaystyle \frac{1}{1+2} \\ \\ &= \displaystyle \frac{2}{3} \\ \\ R’ &= \displaystyle \frac{3}{2} \end{align} \)

と計算できます。

次に，回路全体の合成抵抗の値 \(\displaystyle \frac{6}{10} \ [\Omega]\) から，抵抗 \(R_x\) の値を計算します。

\(\begin{align} \displaystyle \frac{10}{6} &= \displaystyle \frac{1}{R_x} + \displaystyle \frac{1}{R’} \\ \\ &= \displaystyle \frac{1}{R_x} + \displaystyle \frac{1}{\displaystyle \frac{3}{2}} \\ \\ \displaystyle \frac{10}{6} &= \displaystyle \frac{1}{R_x} + \displaystyle \frac{2}{3} \\ \\ \displaystyle \frac{10}{6} \color{red}{ – \displaystyle \frac{2}{3}} &= \displaystyle \frac{1}{R_x} \\ \\ \displaystyle \frac{1}{R_x} &= \displaystyle \frac{10}{6} – \displaystyle \frac{4}{6} \\ \\ &= \displaystyle \frac{6}{6} \\ \\ R_x &= \displaystyle \frac{6}{6} = 1.0 \end{align} \)

となり，抵抗 \(R_x\) の値は \(1\) と求めることができます。