問題
大きさが等しい二つの導体球 A 、 B がある。両導体球に電荷が蓄えられている場合、両導体球の間に働く力は、導体球に蓄えられている電荷の積に比例し、導体球間の距離の 2 乗に反比例する。次の(a)及び(b)の問に答えよ。
ただし、両導体球の大きさは \( \rm 0.3\ m\) に比べて極めて小さいものとする。
(a) この場合の比例定数を求める目的で、導体球 A に\( +2×10^{−8} \ \rm C\) 、導体球 B に\( +3×10^{−8} \ \rm C\) の電荷を与えて、導体球の中心間距離で \( \rm 0.3\ m\) 隔てて両導体球を置いたところ、両導体球間に\( 6×10^{−5} \ \rm N \)の反発力が働いた。この結果から求められる比例定数 \(\rm [N⋅m^2 / C^2] \) として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、導体球 A、, B の初期電荷は零とする。
(1) \(3×10^9\) (2) \(6×10^9\) (3) \(8×10^9\) (4) \(9×10^9\)
(5) \(15×10^9\)
(b) 小問(a)の導体球 A 、 B を、電荷を保持したままで \( \rm 0.3 m\) の距離を隔てて固定した。ここで、導体球 A、 B と大きさが等しく電荷を持たない導体球 C を用意し、導体球 C をまず導体球 A に接触させ、次に導体球 B に接触させた。この導体球 C を図のように導体球 A と導体球 B の間の直線上に置くとき、導体球 C が受ける力が釣り合う位置を導体球 A との中心間距離\(\rm [m]\) で表したとき、その距離に最も近いものを次の(1)~(5)のうちから一つ選べ。
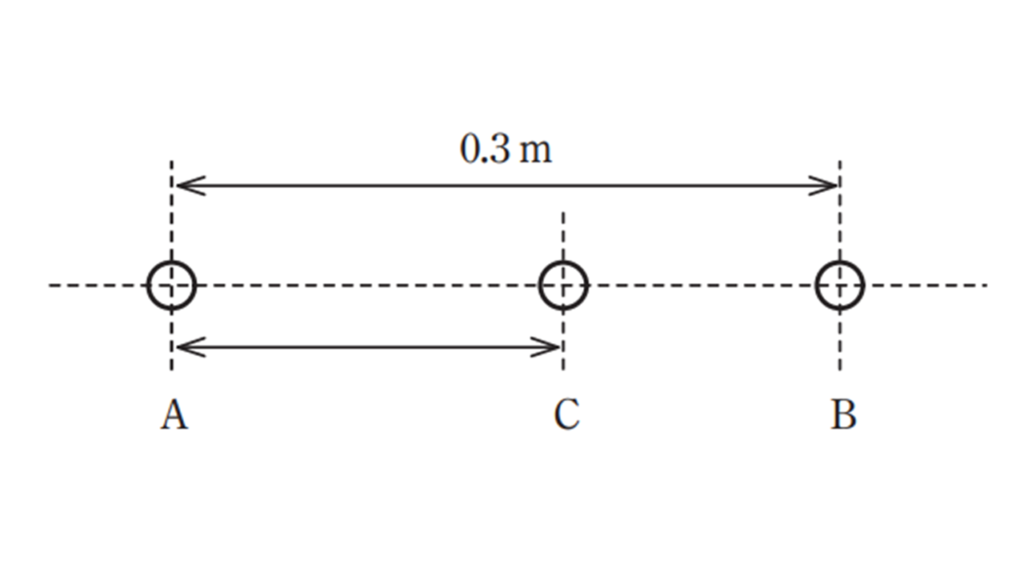
(1) \(0.095\) (2) \(0.105\) (3) \(0.115\) (4) \(0.124\) (5) \(0.135\)
解説
答え:(a)-(4)、(b)-(4)
(a)比例定数を求める
クーロンの法則による、2つの電荷の間にはたらく力の大きさは、導体Aの電荷を\(Q_A\)[C]、導体Bの電荷を\(Q_B\)[C]、誘電率を\(ε\)[F/m]、2つの導体間の距離を\(r\)[m]とすると、以下のように表すことができます。
\( F = \displaystyle \frac{Q_A \times Q_B}{ 4 \pi ε r^2} \)
問題文では、導体A、Bの電荷の大きさと2点間の距離が与えられているので、
\( \displaystyle \frac{1}{4 \pi ε} \)
が比例定数 \(k \rm [N⋅m^2 / C^2] \)となります。
2つの電荷の間にはたらく力の式に与えられた数値を代入して計算すると、
\( \begin{align} F &= \displaystyle \frac{Q_A \times Q_B}{ 4 \pi ε r^2} \\ \\ F &= k \displaystyle \frac{Q_A \times Q_B}{r^2} \\ \\ 6×10^{−5} &= k \displaystyle \frac{2×10^{−8} \times 3×10^{−8} }{ 0.3^2} \\ \\ k &= 6×10^{−5} \times \displaystyle \frac{ 0.3^2}{2×10^{−8} \times 3×10^{−8} } \\ \\ k &= 9\times 10^9 \end{align} \)
よって、(4)が答えとなります。
(b)力のつり合う位置を求める
導体Cに蓄えられる電荷の大きさを求める
Step1) 導体Aと導体Cを接触させたとき
導体Aと導体Cを接触させたときの電荷の移動は、図1のように考えることができます。
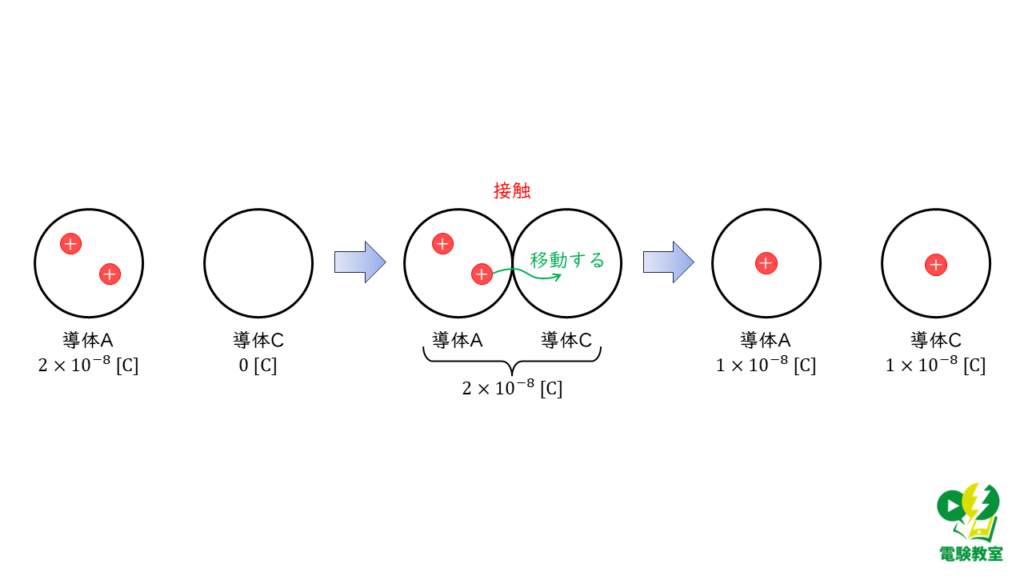
導体AとC接触した直後、それぞれの導体が帯電する電荷は次のようになります。
導体A:\(1 \times 10^{-8} \ \rm C\)
導体C:\(1 \times 10^{-8} \ \rm C\)
Step2) 導体Bと導体Cを接触させたとき
帯電している2つの導体B、Cを接触させたときの電荷の移動は図2のようになります。
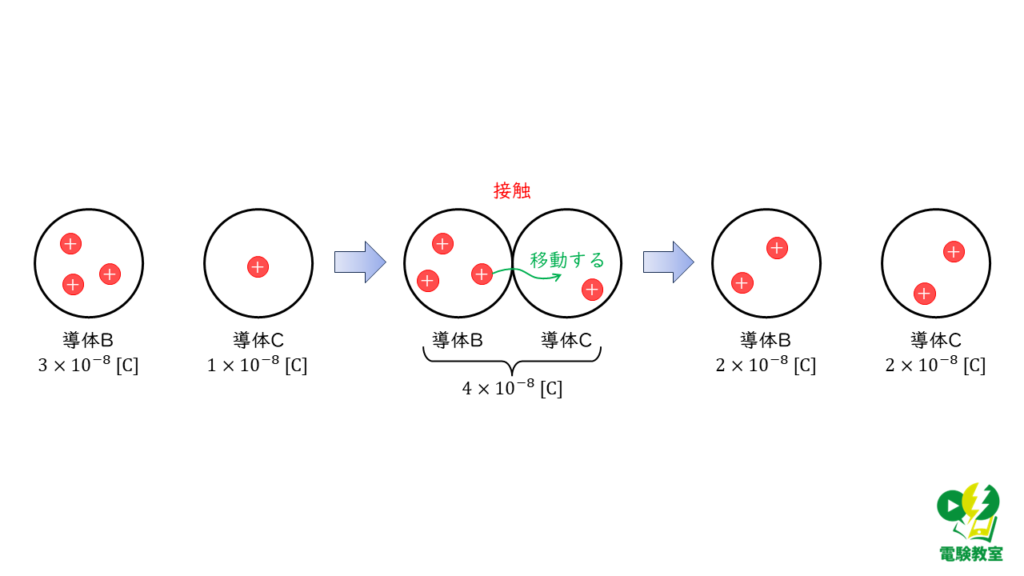
導体BとCが接触した直後、それぞれの導体が帯電する電荷は次のようになります。
導体B:\(2 \times 10^{-8} \ \rm C\)
導体C:\(2 \times 10^{-8} \ \rm C\)
導体Cにはたらく力の大きさが釣り合う点を求める
問題の図のように導体A、B、Cを配置した時、
導体Aと導体Cにはたらく力を\(F_A\)[N]
導体Bと導体Cにはたらく力を\(F_B\)[N]
とすると、それぞれの大きさは、次のようになります。
\( F_A = k \displaystyle \frac{ 1\times 10^{-8}\ \times \ 2 \times 10^{-8} }{r^2} \)
\( F_B = k \displaystyle \frac{ 2\times 10^{-8}\ \times \ 2 \times 10^{-8} }{ \left( 0.3-r \right) ^2} \)
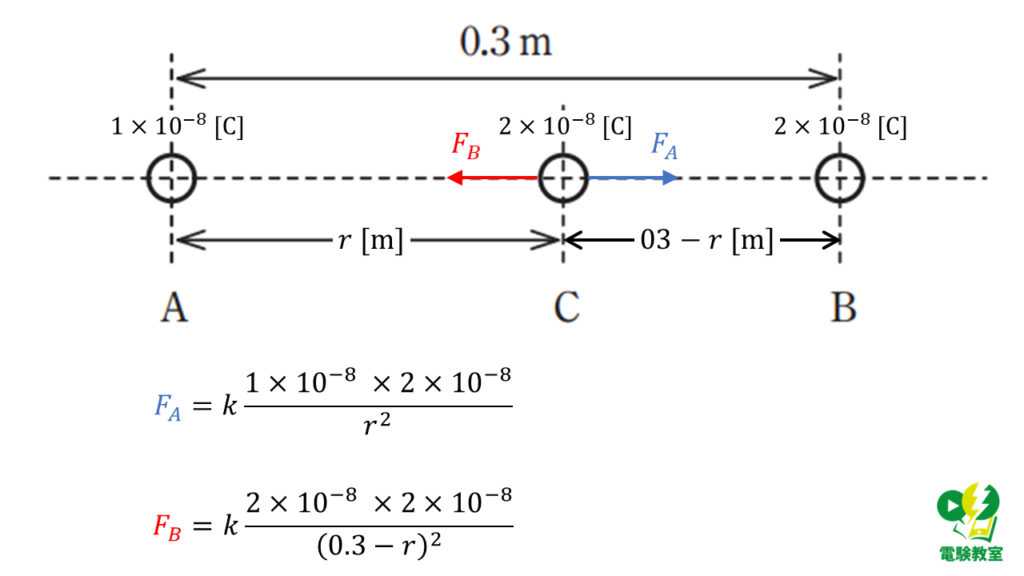
2つの力\(F_A\)と\(F_B\)が釣り合う(大きさが等しくなる)ので、
\( \begin{align} F_A &= F_B \\ k \displaystyle \frac{ 1\times 10^{-8}\ \times \ 2 \times 10^{-8} }{r^2} &= k \displaystyle \frac{ 2\times 10^{-8}\ \times \ 2 \times 10^{-8} }{ \left( 0.3-r \right) ^2} \\ \\ \left( 0.3 – r \right)^2 \times 2\times 10^{-16} &= r^2 \times 4 \times 10^{-16} \\ r^2 -0.6r +0.09 &= 2r^2 \\ r^2 +0.6r -0.09 &= 0 \end{align} \)
二次方程式の解の公式を使い、\(r\)について解くと、
\( \begin{align} r &= \displaystyle \frac{ -0.6 \pm \sqrt{ 0.6^2 -4 \times 1 \times \left( -0.09 \right) } }{ 2 \times 1} \\ \\ &= 0.1242… \approx0.124 \end{align} \)
したがって、答えは(4)となります。











コメント