問題
無限に長い直線状導体に直流電流を流すと,導体の周りに磁界が生じる。この磁界中に小磁針を置くと,小磁針の \( \fbox { (ア) } \) は磁界の向きを指して静止する。そこで,小磁針を磁界の向きに沿って少しずつ動かしていくと,導体を中心とした \( \fbox { (イ) } \) の線が得られる。この線に沿って磁界の向きに矢印をつけたものを \( \fbox { (ウ) } \) という。
また,磁界の強さを調べてみると,電流の大きさに比例し,導体からの \( \fbox { (エ) } \) に反比例している。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
$$ \begin{array}{ccccc} \ &(ア)&(イ)&(ウ)&(エ)\\ \hline (1) &\rm N極 &放射状 &電気力線 &距離の2乗 \\ \hline (2) &\rm N極 &同心円状 &電気力線 &距離の2乗 \\ \hline (3) &\rm S極 &放射状 &磁力線 &距離 \\ \hline (4) &\rm N極 &同心円状 &磁力線 &距離 \\ \hline (5) &\rm S極 &同心円状 &磁力線 &距離の2乗\\ \hline \end{array} $$
解説
答え:(4)
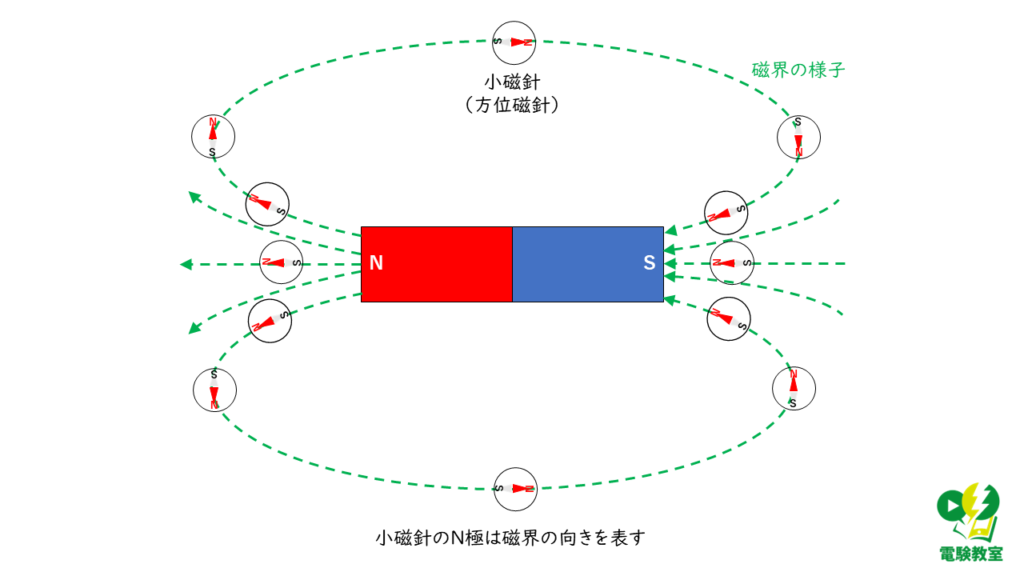
(ア) 磁界の向きと小磁針の向き
磁界中に小磁針(方位磁針)を置くと,小磁針の\(N\)極は,磁界の向きを指します。
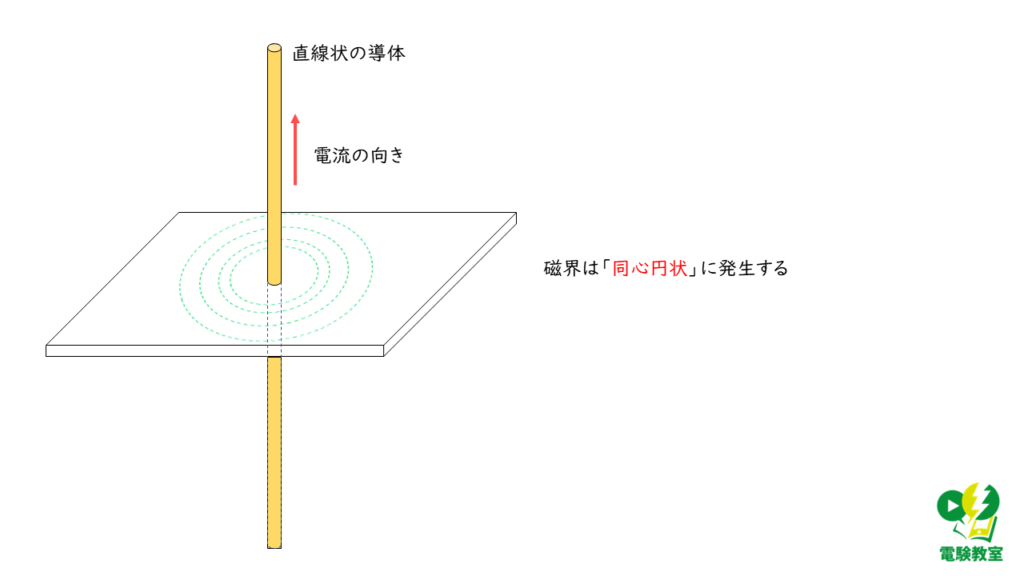
(イ) 直線状導体を流れる電流が作る磁界
直線状導体を流れる電流が作る磁界の向きは下の図のように「同心円状」になります。
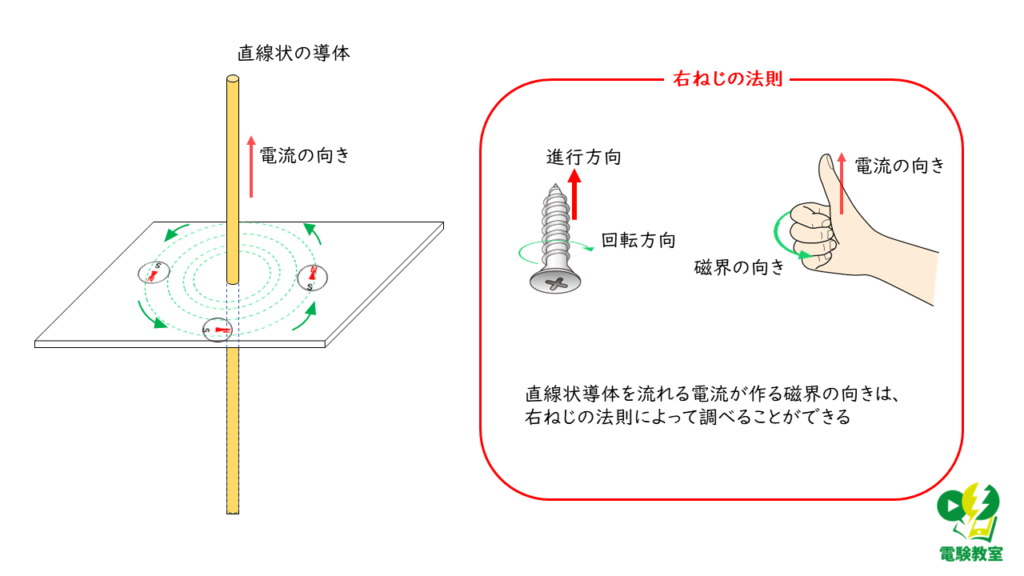
(ウ) 磁界の様子を表す線
磁界の様子を表した線のことを「磁力線」と呼びます。
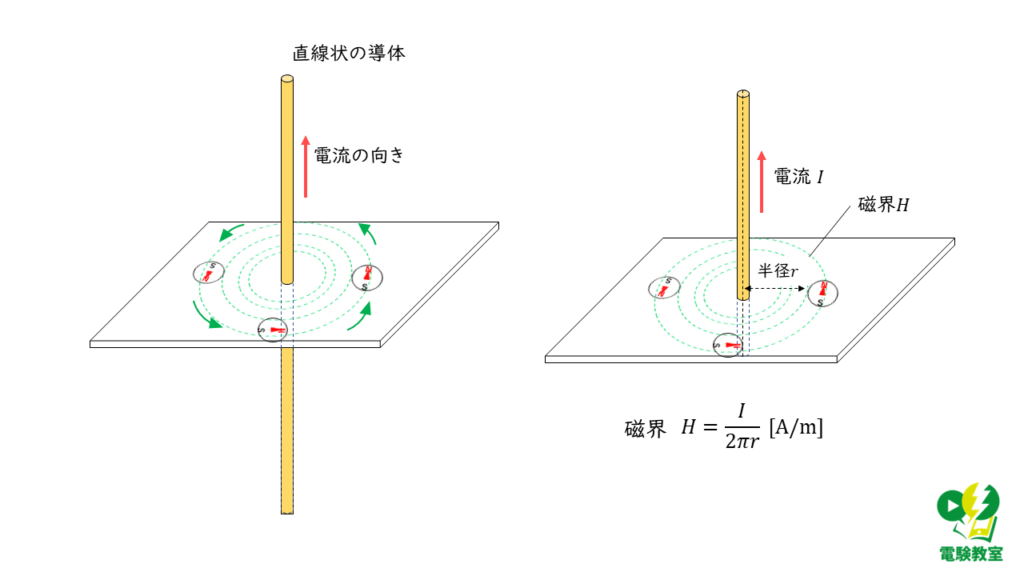
(エ) 直線状導体を流れる電流が作る磁界の大きさ
直線状導体を流れる電流が作る磁界の大きさ \(H\ \rm[A/m]\) は,電流 \(I\ \rm[A]\),導体からの距離 \(r\ \rm[m]\)とすると,
\( H = \displaystyle \frac{I}{2\pi r} \)
で計算することができます。
したがって,磁界の大きさは,電流の大きさに比例し,導体からの距離に反比例します。











コメント