問題
電圧 \(E\ \rm[V]\) の直流電源と静電容量 \(C\ \rm[F]\) の二つのコンデンサを接続した図1,図2のような二つの回路に関して,誤っているものを次の(1)~(5)のうちから一つ選べ。
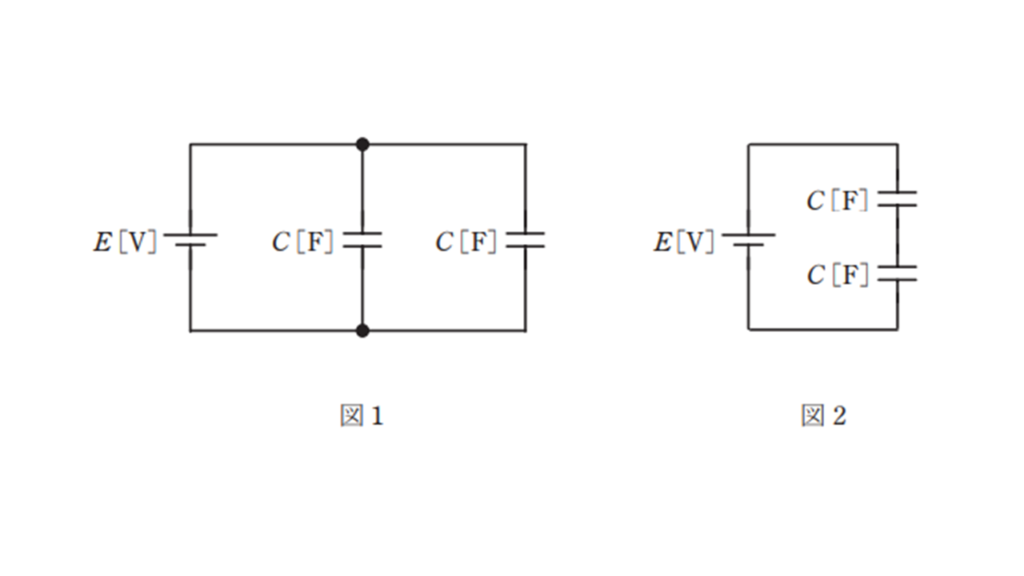
(1) 図1の回路のコンデンサの合成静電容量は,図2の回路の \(4\) 倍である。
(2) コンデンサ全体に蓄えられる電界のエネルギーは,図1の回路の方が図2の回路より大きい。
(3) 図2の回路に,さらに静電容量 \(C\ \rm[F]\) のコンデンサを直列に二つ追加して,四つのコンデンサが直列になるようにすると,コンデンサ全体に蓄えられる電界のエネルギーが図1と等しくなる。
(4) 図2の回路の電源電圧を \(2\) 倍にすると,コンデンサ全体に蓄えられる電界のエネルギーが図1の回路と等しくなる。
(5) 図1のコンデンサ一つ当たりに蓄えられる電荷は,図2のコンデンサ一つ当たりに蓄えられる電荷の \(2\) 倍である。
解説
答え:(3)
コンデンサの合成静電容量について
【図1の場合】

コンデンサは並列接続であるから,合成静電容量 \(C_1 \ \rm [F] \) は,
\( C_1 = C + C = 2C \ \rm [F] \)
【図2の場合】

コンデンサは直セル接続であるから,合成静電容量 \(C_2 \ \rm [F] \) は,
\(C_2 = \displaystyle \frac{C \tiems C}{C + C} = \displaystyle \frac{C}{2} \)
以上のことから,図1の回路の合成静電容量 \(C_1\) は,図2の回路の合成静電容量 \(C_2\) に対して
\(\begin{align} \displaystyle \frac{C_1}{C_2} &= \displaystyle \frac{2C}{\displaystyle \frac{C}{2}} \\ \\ &= \displaystyle \frac{2C \times 2}{C} \\ \\ &= 4 \end{align} \)
となるので,4倍になっていることが計算から求められます。
静電エネルギーの大きさについて
図1,図2それぞれの静電エネルギーの大きさを \(W_1\) , \(W_2\) とすると,
\(\begin{align} W_1 &= \displaystyle \frac{1}{2}C_1 V^2 \\ \\ &= \displaystyle \frac{1}{2} \times 2C V^2 \\ \\ &= CV^2 \end{align} \)
\(\begin{align} W_2 &= \displaystyle \frac{1}{2}C_2 V^2 \\ \\ &= \displaystyle \frac{1}{2} \times \displaystyle \frac{C}{2} V^2 \\ \\ &= \displaystyle \frac{1}{4}CV^2 \end{align} \)
と計算することができます。静電エネルギーの大きさを比べると \( W_1 > W_2\) となるので,図1の方が静電エネルギーが大きいことが分かります。
図2の回路にコンデンサを追加した場合の静電エネルギーの大きさ
問いにあるように,図2の回路に静電容量 \(C\ \rm [F]\) のコンデンサを4つ直列に接続すると回路は以下のようになります。
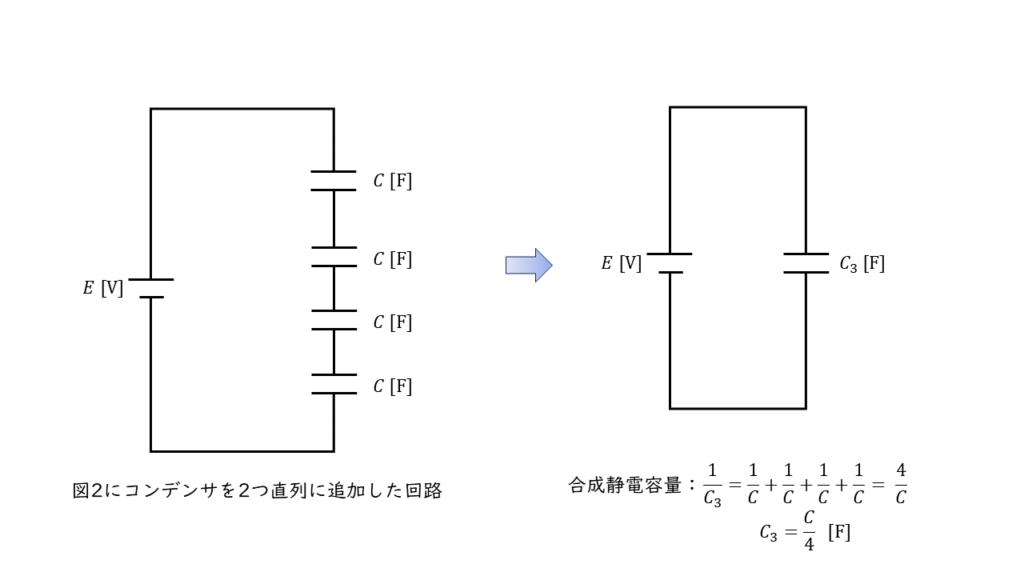
この時の回路全体の静電容量の大きさ \(C_3 \ \rm [F] \) は,
\(\begin{laign} \displaystyle \frac{1}{C_3} &= \displaystyle \frac{1}{C} + \displaystyle \frac{1}{C} + \displaystyle \frac{1}{C} + \displaystyle \frac{1}{C} \\ \\ &= \displaystyle \frac{4}{C} \\ \\ C_4 &= \displaystyle \frac{C}{4} \end{align} \)
となります。したがって,静電エネルギー \(W_3\) の大きさは,
\(\begin{align} W_3 &= \displaystyle \frac{1}{2}C_4 V^2 \\ \\ &= \displaystyle \frac{1}{2} \times \displaystyle \frac{C}{4} V^2 \\ \\ &= \displaystyle \frac{1}{8}CV^2 \end{align} \)
と計算できます。これは図2の静電エネルギー \(W_2 = \displaystyle \frac{1}{4}CV^2\) よりも小さい値であるため,問いの記述は誤りであることが分かります。
図2の回路の電源電圧を \(2\) 倍にしたときの静電エネルギー
電源電圧を \( E\ \rm [V]\) から \(2\) 倍の \(2E\ \rm [V]\) にした場合の静電エネルギーの大きさ \(W_4\) は,
\(\begin{align} W_4 &= \displaystyle \frac{1}{2}C_2 \times \left( 2E \right)^2 \\ \\ &= \displaystyle \frac{1}{2} \times \displaystyle \frac{C}{2} \times 4E^2 \\ \\ &= CV^2 \end{align} \)
と計算できます。したがって,静電エネルギー \(W_4 = W_1\) となるので,(4)の記述は正しいことが分かります。
1つのコンデンサに蓄えられる電荷

図1の回路は,2つのコンデンサが並列に接続されているため,各コンデンサに印加される電圧の大きさは等しく,電源電圧の大きさ \(E\) なります。したがって,1つのコンデンサに蓄えられる電荷量 \(Q_1\ \[C]\) は,
\( Q_1 = C \times E =CE \ \rm [C] \)
と計算できます。
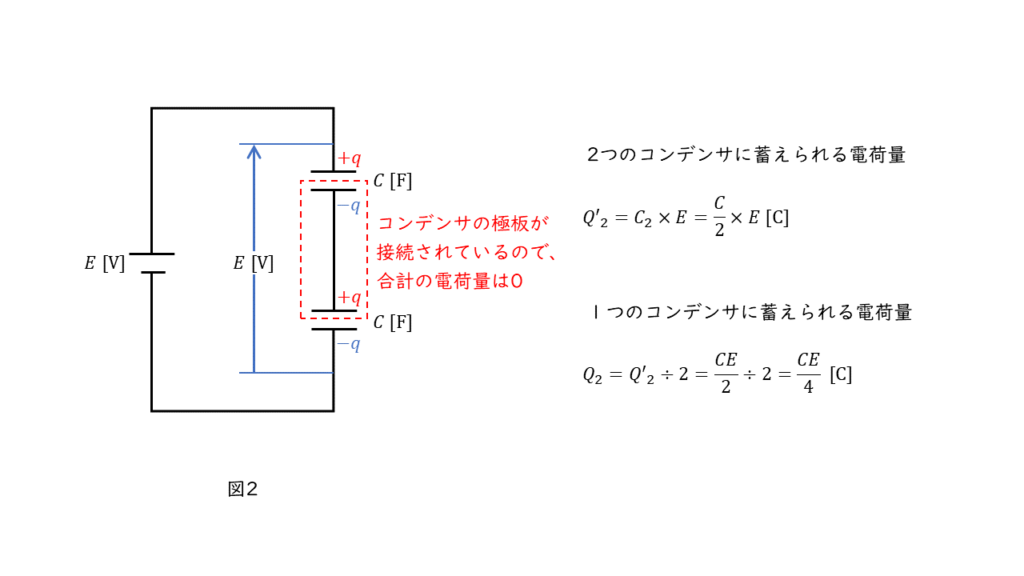
次に,図2の場合は,2つのコンデンサが直列に接続されているので,各コンデンサに蓄えられる電荷量は同じ大きさになります。2つのコンデンサの合計の電荷量 \(Q’_2\ \rm [C]\) は,
\(\begin{align} Q’_1 &= C_2 \times E \\ \\ &= \displaystyle \frac{C}{2} \times E \\ \\ &= \displaystyle \frac{CE}{2} \end{align} \)
となります。
2つのコンデンサの合計の電荷量が \(Q_1 = \displaystyle \frac{CE}{2} \) であるから,1つのコンデンサあたりの電荷量 \(Q_1\) は,
\(\begin{align} Q_1 &= Q’_1 \div 2 \\ \\ &= \displaystyle \frac{CE}{2} \times \displaystyle \frac{1}{2} \\ \\ &= \displaystyle \frac{CE}{4} \end{align} \)
図1と図2のコンデンサ1つあたりに蓄えられる電荷量を比較すると,
\( \begin{align} \displaystyle \frac{Q_1}{Q_2} &= \displaystyle \frac{CE}{\displaystyle \frac{CE}{4}} \\ \\ &= \displaystyle \frac{CE \times 4}{\displaystyle \frac{CE}{4} \times 4} \\ \\ &= \displaystyle \frac{4}{1} \\ \\ &= 4 \end{align} \)
となるため,図1の1つのコンデンサが蓄える電荷量は,図2の1つのコンデンサが蓄える電荷量の4倍であることが分かります。











コメント