問題
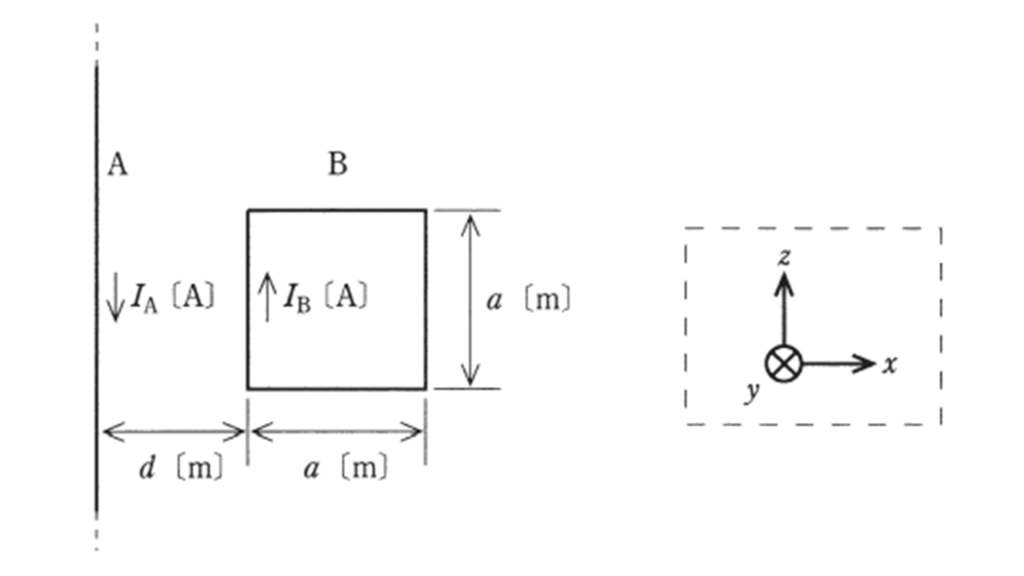
図のように,透磁率 \(\mu_0 \ \rm[H/m]\) の真空中に無限に長い直線状導体 \(A\) と \(1\) 辺 \(a\ \rm[m]\) の正方形のループ状導体 \(B\) が距離 \(d\ \rm[m]\) を隔てて置かれている。 \(A\) と \(B\) は \(xz\) 平面上にあり, \(A\) は \(z\) 軸と平行, \(B\) の各辺は \(x\) 軸又は \(z\) 軸と平行である。
\(A\) ,\(B\) には直線電流 \(I_A\ \rm[A]\) , \(I_B\ \rm[A]\) が,それぞれ図示する方向に流れている。このとき, \(B\) に加わる電磁力として,正しいものを次の(1)~(5)のうちから一つ選べ。
なお, \(xyz\) 座標の定義は,破線の枠内の図で示したとおりとする。
(1) \(0\ \rm [N]\) つまり電磁力は生じない
(2) \(\displaystyle \frac{\mu_0 I_A I_B a^2 }{2\pi d\left( a + d \right) } \ \rm [N]\) の \(+x\) 方向の力
(3) \(\displaystyle \frac{\mu_0 I_A I_B a^2}{2\pi d \left( a + d \right)} \ \rm[N]\) の \(−x\) 方向の力
(4) \(\displaystyle \frac{\mu_0 I_A I_B a \left( a + 2d \right)}{2\pi d \left( a + d \right)} \ \rm[N]\) の \(+x\) 方向の力
(5) \(\displaystyle \frac{\mu_0 I_A I_B a \left( a + 2d \right)}{2\pi d \left( a + d \right)} \ \rm[N]\) の \(−x\) 方向の力
解説
答え:(2)
ループ状導体のどの辺に電磁力が発生するかを考える
問いの図より,直線状導体 \(A\) 電流が流れるとその周囲には磁界が発生するため,直線状導体 \(A\) と平行な位置関係にあるループ導体 \(B\) の辺には電磁力が発生することが考えられます。
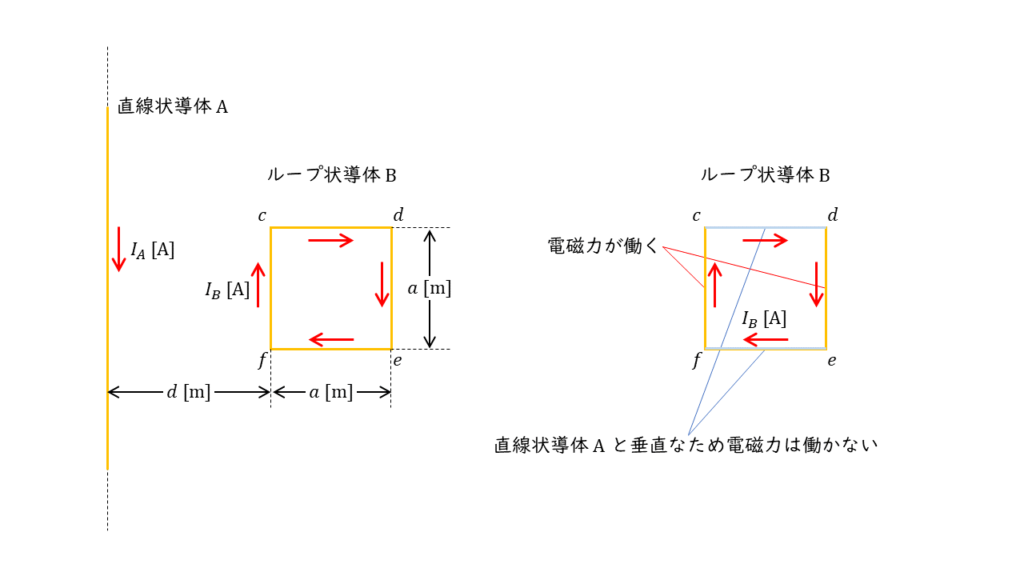
各辺にはたらく電磁力の大きさを求める
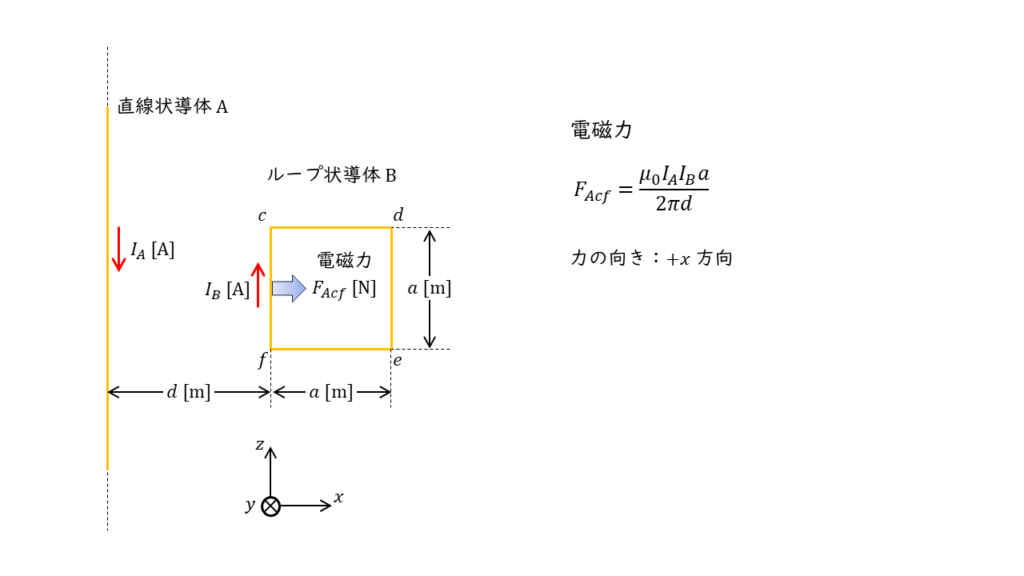
辺 \(cf\) は,直線状導体 \(A\) と反対法に電流が流れるため,電磁力の力の向きは \(+x\) 方向になります。
この時の電磁力の大きさ \( F_{Acf} \) は,
\( F_{Acf} = \displaystyle \frac{\mu_0 I_A I_B a}{2\pi d} \)
となります。
一方,ループ導体の辺 \(de\) には,直線状導体 \(A\) と同じ方向に電流が流れるため,\(-x\) 方向に電磁力が働きます。
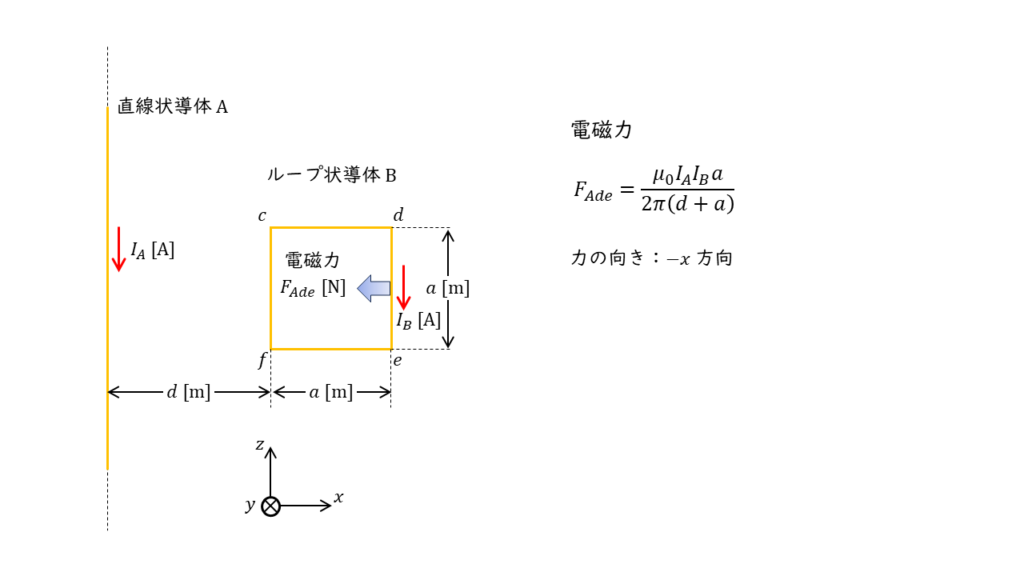
この時の電磁力の大きさ \(F_{Ade}\) は,
\( F_{Ade} = \displaystyle \frac{\mu_0 I_A I_B a }{2 \pi \left( d+a \right)} \)
となります。
ループ導体 \(B\) にはたらく合計の電磁力を求める
各辺にはたらく電磁力の向きはそれぞれ逆向きであるので,合計の電磁力 \(F\) は,
\( \begin{align} F &= F_{Acf} – F_{Ade} \\ \\ &= \displaystyle \frac{\mu_0 I_A I_B a}{2\pi d} – \displaystyle \frac{\mu_0 I_A I_B a }{2 \pi \left( d+a \right)} \\ \\ &= \displaystyle \frac{\mu_0 I_A I_B a \times \left(d +a \right) }{2 \pi a \times \left( d+a \right)} – \displaystyle \frac{\mu_0 I_A I_B a \times d }{2 \pi \left( d+a \right) \times d} \\ \\ &= \displaystyle \frac{\mu_0 I_A I_B a \lbrace \left(d+a\right) – d \rbrace }{2 \pi d \left( d+a \right)} \\ \\ &= \displaystyle \frac{\mu_0 I_A I_B a^2 }{2 \pi d \left( d+a \right)} \end{align} \)
と計算できます。計算の結果,合計した電磁力の大きさは「正の値」であるから,力の向きは \(+x\) 方向となります。
したがって,答えは(2)となります。











コメント