【過去問解説】R4下期理論　問7　抵抗値の温度変化による補正の計算問題

問題

 \(20\) ℃ における抵抗値が \(R_1\ [\Omega]\) ，抵抗温度係数が \(\alpha_1\ \rm[℃^{−1}]\) の抵抗器 \(\rm A\) と \(20\) ℃ における抵抗値が \(R_2\ [\Omega]\) ，抵抗温度係数が \(\alpha_2 = 0\ \rm ℃^{−1} \) の抵抗器 \(B\) が並列に接続されている。その \(20\) ℃ と \(21\) ℃ における並列抵抗値をそれぞれ \(r_{20} \ [\Omega]\) ， \(r_{21}\ [\Omega]\) とし，\( \displaystyle \frac{r_{21}−r_{20}}{r_{20}} \) を変化率とする。この変化率として，正しいものを次の(1)～(5)のうちから一つ選べ。

\( \begin{align} &(1)　\displaystyle \frac{\alpha_1 R_1 R_2}{R_1 + R_2 +\alpha_1 ^2 R_1} 　 &(2)　\displaystyle \frac{\alpha_1 R_2}{R_1 + R_2 \alpha_1 R_1} \\ \\ &(3)　\displaystyle \frac{\alpha_1 R_1}{R_1 + R_2 \alpha_1 R_1} 　 &(4)　\displaystyle \frac{\alpha_1 R_2}{R_1 + R_2 \alpha_1 R_2} \\ \\ &(5)　\displaystyle \frac{\alpha_1 R_1}{R_1 + R_2 \alpha_1 R_2} \end{align} \)

解説

答え：（2）

抵抗A，Bの値を求める式

温度変化を \(\Delta t \) ℃ で表すとすると，ある温度における抵抗A，Bの抵抗値 \(R_A \ \Omega \) ，\(R_B \ \Omega\) は以下の式で表すことができます。

\( R_A = R_1 \times \left( 1 + \alpha_1 \Delta t \right) \)

\( R_B = R_2 \times \left( 1 + \alpha_2 \Delta t \right) = R_2 \times \left( 1 + 0 \times \Delta t \right) = R_2 \)

20℃に時の合成抵抗の値

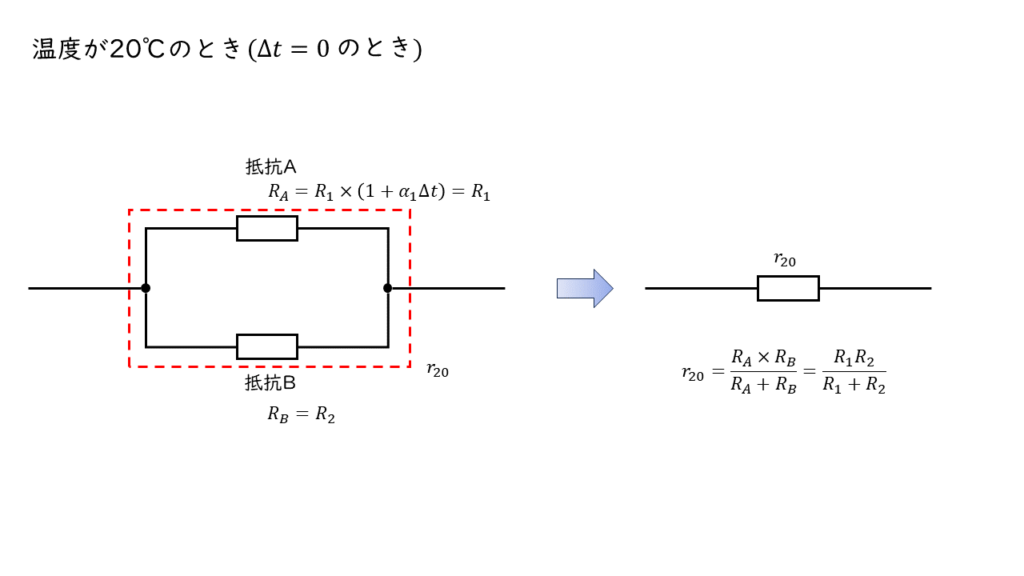
温度20℃の時に抵抗A，Bの大きさはそれぞれ，

\(R_A = R_1 \ \Omega\)

\( R_B = R_2 \ \Omega\)

となります。この2つの抵抗をを並列接続したときの合成抵抗 \(r_{20} \) の大きさは，

\(\begin{align} \displaystyle \frac{1}{r_{20}} &= \displaystyle \frac{1}{R_A} + \displaystyle \frac{1}{R_B} \\ \\ &= \displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} \\ \\ &= \displaystyle \frac{R_2 + R_1}{R_1 \times R_2} \\ \\ r_{20} &= \displaystyle \frac{R_1 R_2}{R_1 +R_2} \end{align} \)

と計算できます。

21℃に時の合成抵抗の値

温度20℃の時に抵抗A，Bの大きさはそれぞれ，

\(\begin{align}R’_A &= R_1 \times \left( 1 + \alpha_1 \Delta t \right) \\ &=R_1 \times \left( 1 + \alpha_1 \times 1 \right) \\ &= R_1 \left( 1 + \alpha_1 \right) \ \Omega \end{align}\)

\( R’_B = R_2 \ \Omega\)

となります。この2つの抵抗をを並列接続したときの合成抵抗 \(r_{21} \) の大きさは，

\( \begin{align} \displaystyle \frac{1}{r_{21}} &= \displaystyle \frac{1}{R’_A} + \displaystyle \frac{1}{R’_B} \\ \\ &= \displaystyle \frac{1}{R_1 \times \left( 1 + \alpha_1 \times 1 \right) } + \displaystyle \frac{1}{R_2} \\ \\ &= \displaystyle \frac{R_2 + R_1 \times \left( 1 + \alpha_1 \times 1 \right)}{R_1 \times \left( 1 + \alpha_1 \times 1 \right) \times R_2} \\ \\ r_{21} &= \displaystyle \frac{R_1 \times \left( 1 + \alpha_1 \times 1 \right) \times R_2}{R_1 \times \left( 1 + \alpha_1 \times 1 \right) + R_2 } \end{align} \)

となります。

\( \displaystyle \frac{r_{21} – r_{20} }{r_{20}}\) の値を求める

\( \begin{align} \displaystyle \frac{ r_{21} – r_{20} }{ r_{20} } &= \displaystyle \frac{\displaystyle \frac{R_1 \times \left( 1 + \alpha_1 \times 1 \right) \times R_2}{R_1 \times \left( 1 + \alpha_1 \times 1 \right) + R_2 } – \displaystyle \frac{R_1 R_2}{R_1 + R_2}}{\displaystyle \frac{R_1 R_2}{R_1 + R_2}} \\ \\ &= \displaystyle \frac{\displaystyle \frac{R_1 \times \left( 1 + \alpha_1 \times 1 \right) \times R_2}{R_1 \times \left( 1 + \alpha_1 \times 1 \right) + R_2 } \color{red}{\times \displaystyle \frac{R_1 + R_2}{R_1 R_2}} – \displaystyle \frac{R_1 R_2}{R_1 + R_2} \color{red}{\times \displaystyle \frac{R_1 + R_2}{R_1 R_2}}}{\displaystyle \frac{R_1 R_2}{R_1 + R_2} \color{red}{ \times \displaystyle \frac{R_1 + R_2}{R_1 R_2}}} \\ \\ &= \displaystyle \frac{\left(1 + \alpha_1 \right)\left(R_1+R_2 \right)}{\left(1 + \alpha_1 \right)R_1 + R_2} – 1 \\ \\ &= \displaystyle \frac{\left(1 + \alpha_1 \right)\left(R_1+R_2 \right) – \left(1 + \alpha_1 \right)R_1 + R_2}{\left(1 + \alpha_1 \right)R_1 + R_2} \\ \\ &= \displaystyle \frac{}{R_1 + R_2 + \alpha_1 R_1} \end{align} \)

以上のように計算できるので，答えは(2)となります。