問題
真空中に, \(2\) 本の無限長直線状導体が \(20\ \rm[cm]\) の間隔で平行に置かれている。一方の導体に \(10\ \rm[A]\) の直流電流を流しているとき,その導体には \(1\ \rm[m]\) 当たり \(1 \times 10^{−6} \ \rm[N]\) の力が働いた。他方の導体に流れている直流電流 \(I\ \rm[A]\) の大きさとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,真空の透磁率は \(\mu_0 = 4 \pi \times 10^{−7} \ \rm[H/m]\) である。
(1) \(0.1\) (2) \(1\) (3) \(2\) (4) \(5\) (5) \(10\)
解説
答え:(1)
2本の平行な直線導体にはたらく電磁力
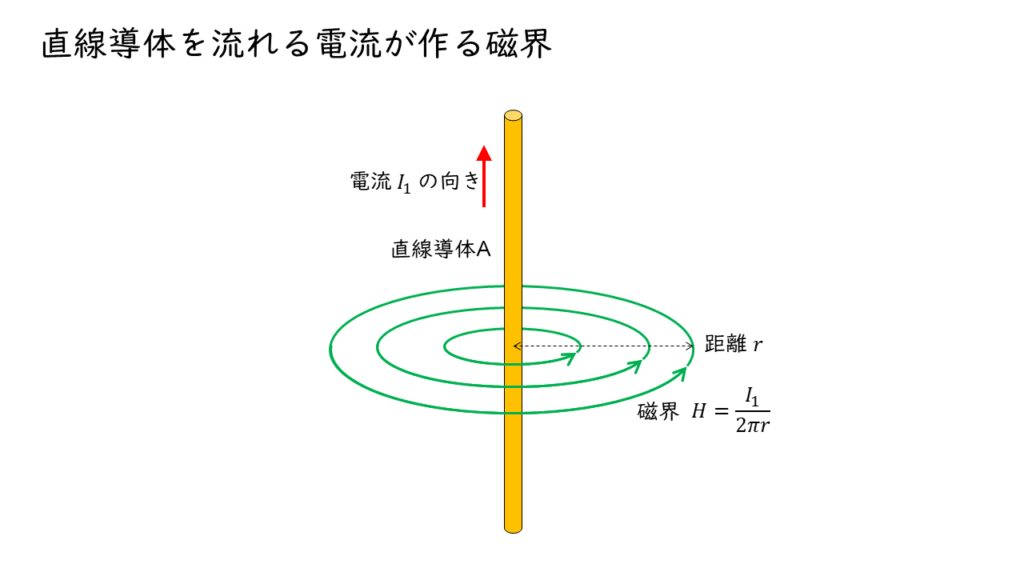
上図のように,直線導体Aに電流が流れると,導体の周囲に磁界\(H \ \rm A/m\) が発生します。この磁界の大きさは,導体を流れる電流を \(I_1\ \rm A\) ,導体からの距離を \(r\ \rm m\) とすると,
\( H = \displaystyle \frac{I_1}{2 \pi r} \)
となります。
この磁界中に,下図のように電流が流れる直線導体Bを置くと,電流と磁界が作用し,各導体に電磁力 \(F\) が生じます。
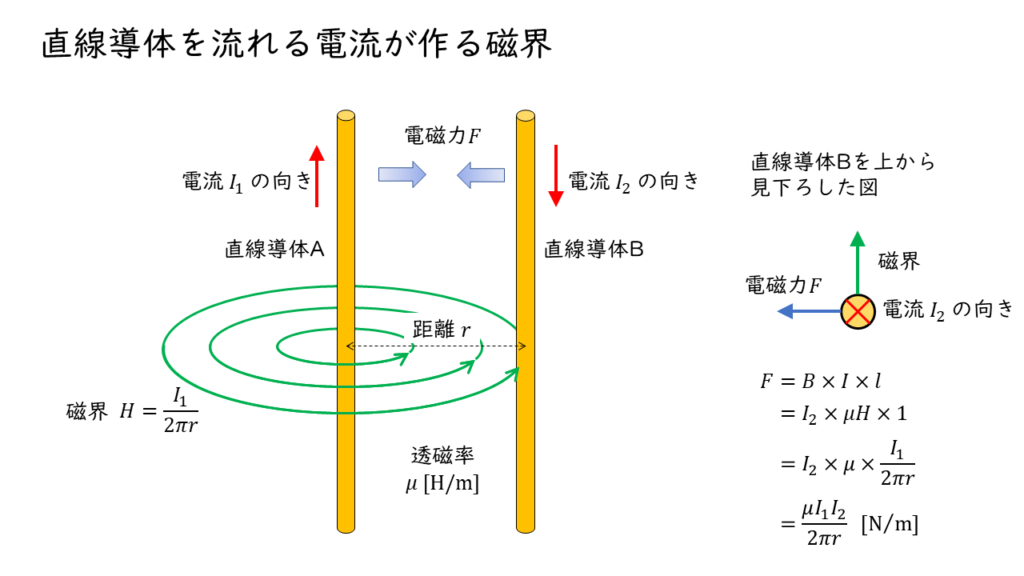
導体 \(1\ \rm m\) あたりにはたらく電磁力 \(F \ \rm N\) の大きさは,直線導体Bを流れる電流を \(I_2 \ \rm A\),透磁率を \(\mu H/m\) ,とすると,
\(\begin{align} F&= I \times B \times 1 \\ &= I_2 \times \mu H \\ &= I_2 \times \mu \times \displaystyle \frac{I_1}{2 \pi r} \\ &= \displaystyle \frac{\mu I_1 I_2}{2 \pi r} \ \rm[N/m] \end{align} \)
と計算することができます。
問題の条件を電磁力の式に当てはめると,
\(\begin{align} F &= \displaystyle \frac{\mu I_1 I_2}{2 \pi r} \\ \\ 1.0 \times 10^{-6} &= \displaystyle \frac{4 \pi \times 10^{-7} \times 10 \times I_2 }{2 \pi \times 0.2} \\ \\ I_2 &= \displaystyle \frac{1.0 \times 10^{-6} \times 0.4 \pi}{4 \pi \times 10^{-6}} \\ \\ I_2 &= 0.1 \end{align} \)
となり,答えは(1)になります。











コメント