問題
環状鉄心に絶縁電線を巻いて作った磁気回路に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
(1) 磁気抵抗は,磁束の通りにくさを表している。毎ヘンリー \(\rm[H^{−1}]\) は,磁気抵抗の単位である。
(2) 電気抵抗が導体断面積に反比例するように,磁気抵抗は,鉄心断面積に反比例する。
(3) 鉄心の透磁率が大きいほど,磁気抵抗は小さくなる。
(4) 起磁力が同じ場合,鉄心の磁気抵抗が大きいほど,鉄心を通る磁束は小さくなる。
(5) 磁気回路における起磁力と磁気抵抗は,電気回路におけるオームの法則の電流と電気抵抗にそれぞれ対応する。
解説
答え:(5)
磁気抵抗とは
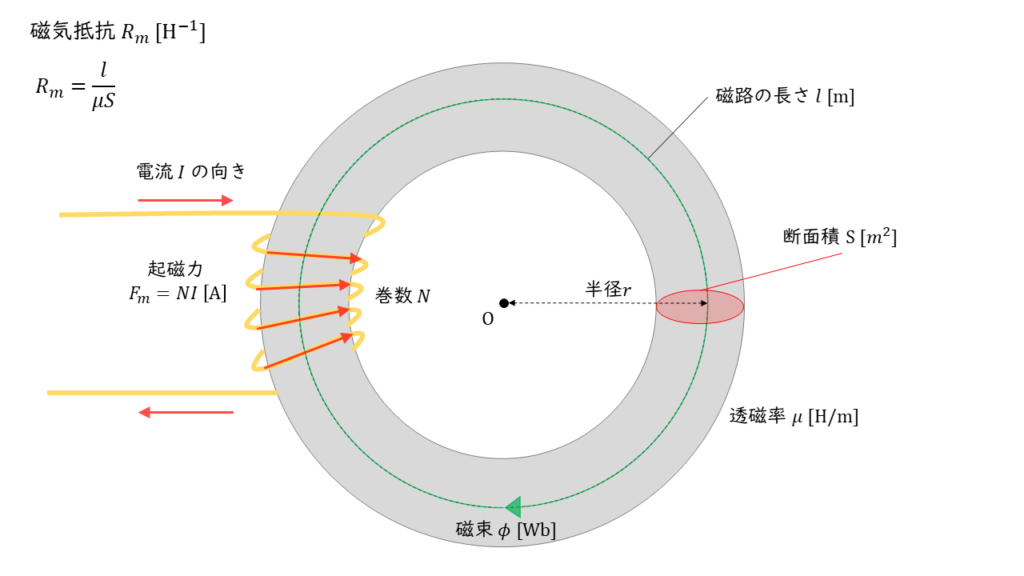
磁気抵抗 \(r_m\) は,磁束の通りにくさを表します。環状鉄心の断面積を \(S\ \rm m^2\) ,平均の磁路長を \(l\ \rm m\) ,透磁率を \( \mu \ \rm H/m\) とすると,磁気抵抗は以下の式で表すことができます。
\( R_m = \displaystyle \frac{l}{\mu S} \)
上記の式から,磁気抵抗の単位は
\( \displaystyle \frac{\rm m}{\rm H/m \times m^2} = \displaystyle \frac{\rm m}{\rm H \times m} = \displaystyle \frac{1}{H} = H^{-1} \)
と考えられるので,「(1)は正しい」です。
磁気回路と電気回路の比較
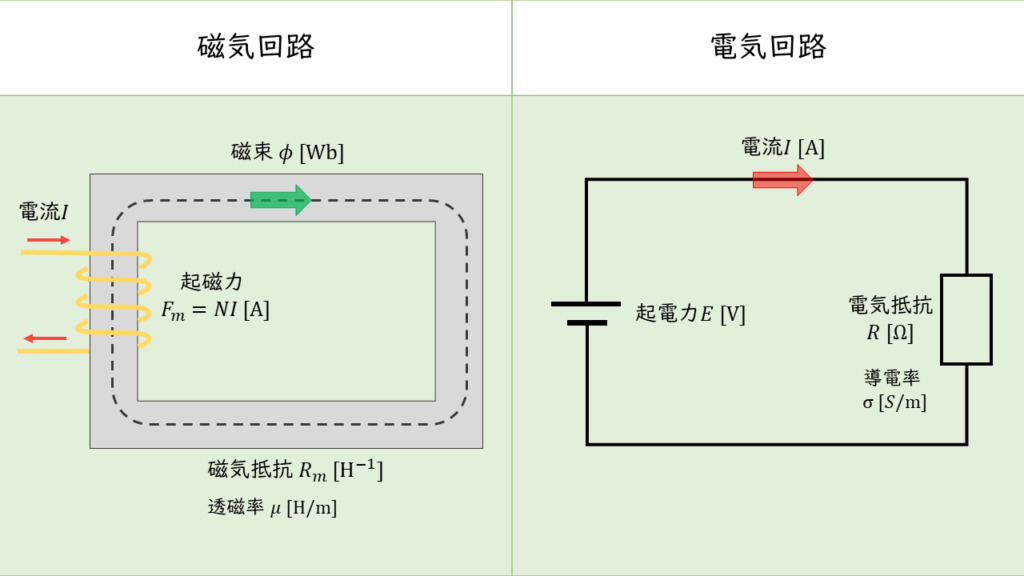
上図から分かるように磁気回路と電気回路は同じように考えることができ,それぞれ以下のように対応しています。
| 電気回路 | 磁気回路 |
| 電圧 \(E \ \rm[V]\) | 起磁力 \(NI \ \rm[A]\) |
| 電流 \(I \ \rm [A]\) | 磁束 \( \phi \ \rm[Wb]\) |
| 抵抗 \( R \ \rm [\Omega]\) | 磁気抵抗 \( R_m \ \rm[H^{-1}]\) |
| 導電率 \( \sigma \ \rm [S/m]\) | 透磁率 \( \mu \ \rm [H/m[\) |
電気抵抗は,抵抗の断面積を \(S\ \rm m^2\) ,抵抗の長さを \(l\ \rm m\) ,導電率 \(\sigma \ \rm S/m\) とすると,
\( R = \displaystyle \frac{l}{\sigma S}\)
となります。磁気抵抗 \(R_m\)は,
\( R_m = \displaystyle \frac{l}{\mu S} \)
のしきで表すことができましたから,電気回路も磁気回路も「抵抗の大きさは,断面積に反比例する」といえます。よって,「(2)も正しい」です。
また,磁気回路と電気回路はそれぞれ上の表のように対応しているので,「(5)は誤り」であることがわかります。
透磁率とは
透磁率とは,磁束の通しやすさを表します。透磁率が大きいほど,磁束が通りやすくなるので,磁気抵抗は小さくなります。このことは磁気抵抗の式からも読み取れます。
したがって、「(3)も正しい」といえます。
磁束 \( \phi\) を求める式
磁気回路のオームの法則から,磁束 \( \phi\) は,起磁力を \(NI\) ,磁気抵抗を \(R_m\)とすると,
\( \phi = \displaystyle \frac{NI}{R_m} \)
と書き表すことができます。上記の式より,磁気抵抗 \(R_m\) が大きくなるほど磁束 \(\phi\) は小さくなるので,「(4)も正しい」といえます。











コメント