問題
図のように,十分に長い直線状導体 \(A\) ,\(B\) があり,\(A\) と \(B\) はそれぞれ直角座標系の \(x\) 軸と \(y\) 軸に沿って置かれている。 \(A\) には \(+x\) 方向の電流 \(I_x\ \rm [A]\) が,\(B\) には \(+y\) 方向の電流 \(I_y\ \rm[A]\) が,それぞれ流れている。\(I_x > 0\) ,\(I_y > 0\) とする。
このとき,\(xy\) 平面上で \(I_x\) と \(I_y\) のつくる磁界が零となる点 \( \left( x\ \rm{[m]} , y \ \rm{[m]} \right) \) の満たす条件として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,\(x \neq 0 , y \neq 0 \)とする。

(1) \( y = \displaystyle \frac{I_x}{I_y}x \) (2) \( y = \displaystyle \frac{I_y}{I_x}x \) (3) \( y = -\displaystyle \frac{I_x}{I_y}x \) (4) \( y = -\displaystyle \frac{I_y}{I_x}x \) (5) \( y = \pm x \)
解説
答え:(1)
直線導体 \(A\) を流れる電流の作る磁界
直線導体 \(A\) を流れる電流が,導体からの距離 \( x\ \rm m\) の地点に作る磁界の大きさ \(H_A \ \rm [A/m]\) は,
\( H_A = \displaystyle \frac{I_x}{2 \pi x} \)
となります。また,磁界の向きは『右ねじの法則』によって求められるので,磁界の様子を問いの図に書き入れると,以下のようになります。

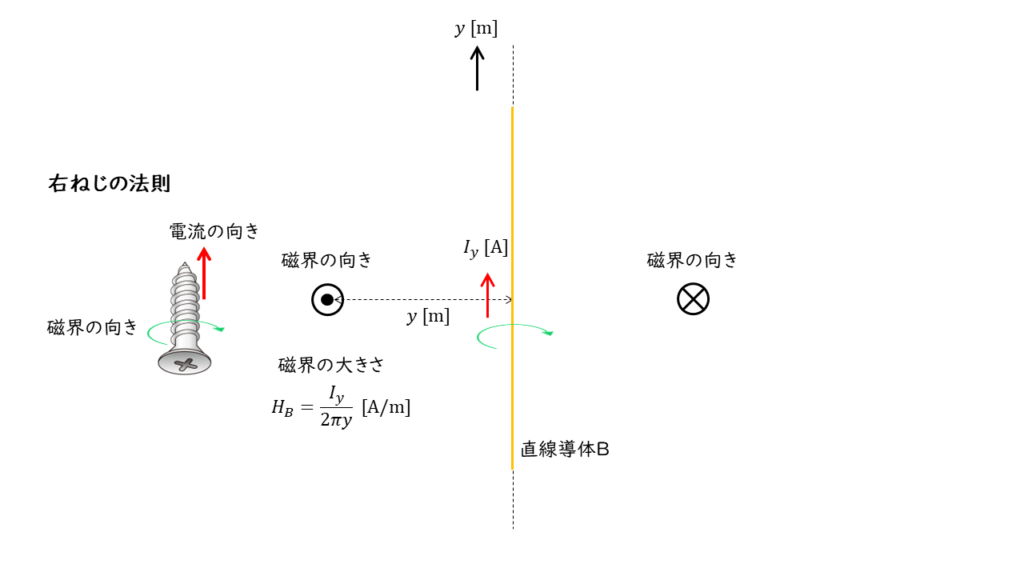
直線導体 \(B\) を流れる電流の作る磁界
直線導体 \(B\) を流れる電流が,導体からの距離 \(y\ \rm m\) の地点に作る磁界の大きさ \(H_B \ \rm [A/m]\) は,
\( H_B = \displaystyle \frac{I_y}{2 \pi y} \)
となります。また,磁界の向きは『右ねじの法則』によって求められるので,磁界の様子を問いの図に書き入れると,以下のようになります。
磁界 \(H_A , H_B \) の合成した磁界の大きさを考える
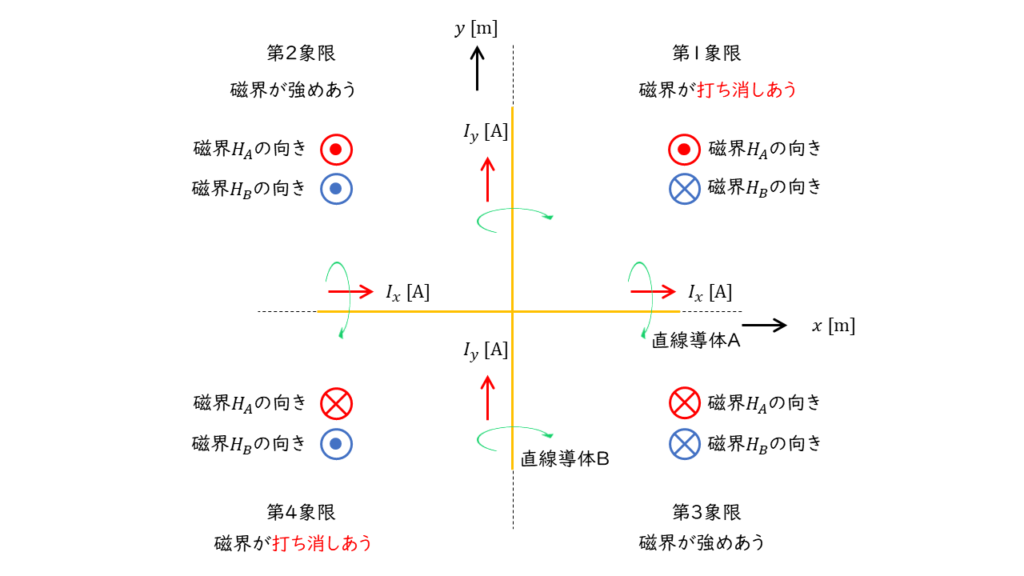
2つの磁界を1つの平面図上に書き入れると,以下のようになり \(xy\) 平面上の第1象限と第4象限では2つの磁界が互いに打ち消しあう方向となります。したがって,第1象限と第4象限の領域内では,2つの磁界の合計が \(0\) となります。
上記の関係を磁界の大きさを式を使って表すと,
\(\begin{align} H_A – H_B &= 0 \\ \displaystyle \frac{I_x}{2 \pi x} – \displaystyle \frac{I_y}{2 \pi y} &= 0 \\ \\ \displaystyle \frac{I_y}{2 \pi y} &= \displaystyle \frac{I_x}{2 \pi x} \\ \\ I_y x &=I_x y \\ y &= \displaystyle \frac{I_y}{I_x}x \end{align} \)
したがって,答えは(1)となります。











コメント