問題
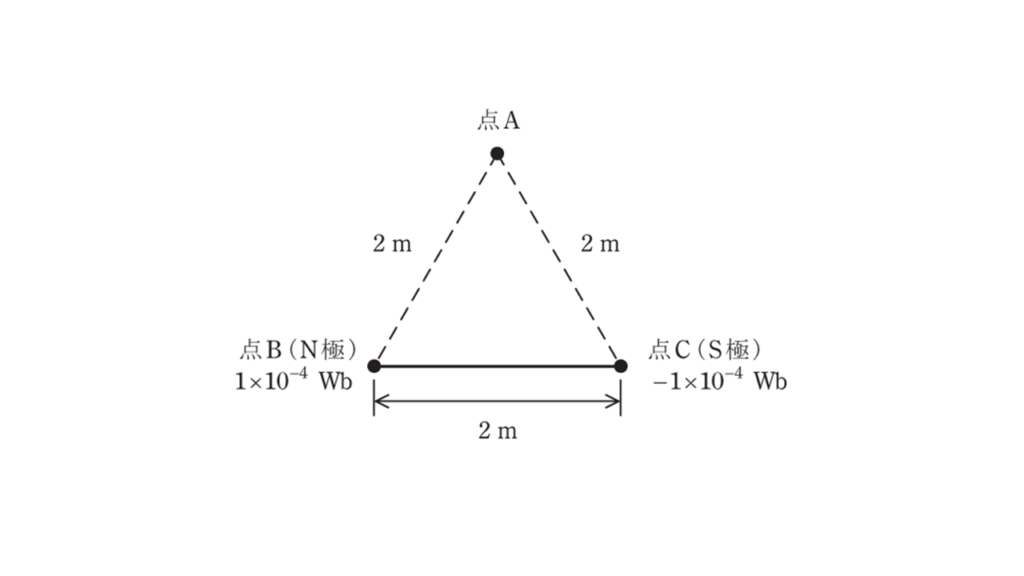
長さ \(2\ \rm m\) の直線状の棒磁石があり,その両端の磁極は点磁荷とみなすことができ,その強さは,N極が \(1×10^{-4}\ \rm Wb\) ,S極が \(-1×10^{-4}\ \rm Wb\) である。図のように,この棒磁石を点 \(BC\) 間に置いた。このとき,点 \(A\) の磁界の大きさの値 \(\rm [A/m]\) として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,点 \(A\) ,\(B\) ,\(C\) は,一辺を \(2\ \rm m\) とする正三角形の各頂点に位置し,真空中にあるものとする。真空の透磁率は \(μ_0 = 4 \pi×10^{-7} \ \rm H/m\) とする。また,N極,S極の各点磁荷以外の部分から点 \(A\) への影響はないものとする。
(1) \(0\) (2) \(0.79\) (3) \(1.05\) (4) \(1.58\) (5) \(3.16\)
解説
答え:(4)
点 \(B\) の磁極による磁力の大きさと向きを求める
磁力の大きさ \(F\ \rm N\) は,磁極1が持つ磁束を \(m_1 \ \rm Wb\) ,磁極2が持つ磁束を \(m_2 \ \rm Wb\) ,磁極間の距離を \(r\ \rm m\) ,透磁率を \(μ \ \rm H/m\) とすると,
\( F = \displaystyle \frac{m_1 \times m_2}{4 \pi μ r^2} \)
で求めることができます。
したがって,磁極 \(B\) と磁極 \(A\) の間に働く力の大きさは,
\( \begin{align} \vert F_{AB} \vert &= \displaystyle \frac{m_A \times m_B}{4 \pi μ_0 r^2} \\ \\ &= \displaystyle \frac{1×10^{-4} \times 1×10^{-4}}{4 \pi \times 4 \pi×10^{-7} \times 2^2 } \\ \\ &= 1.583 \ \rm N \end{align} \)
磁極 \(A\) ,\(B\) はともにN極であるから,磁極間にはたらく力の種類は斥力となり、下図のようになります。

点 \(C\) の磁極による磁力の大きさと向きを求める
磁極 \(C\) と磁極 \(A\) の間に働く力の大きさは,
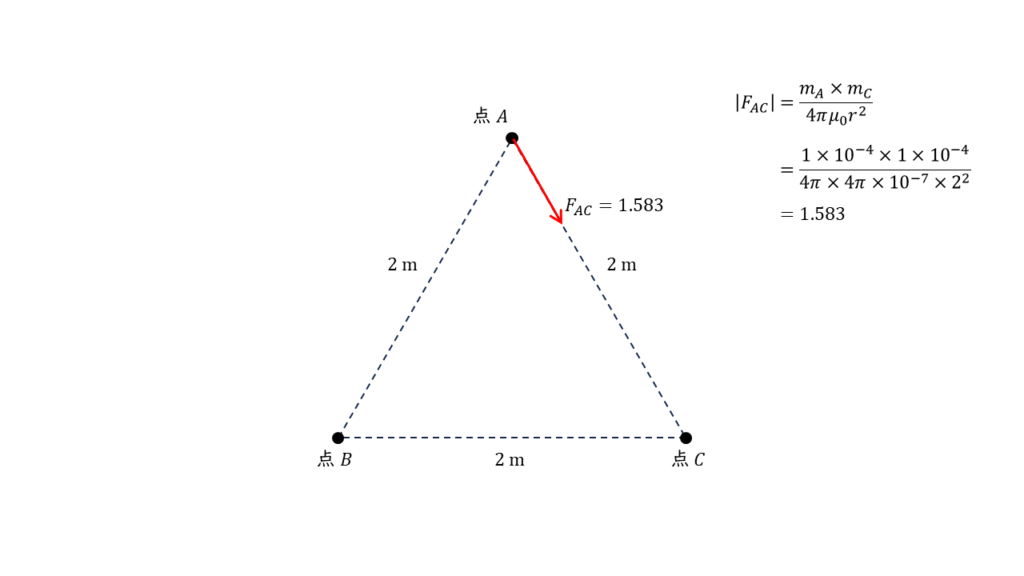
\( \begin{align} \vert F_{AC} \vert &= \displaystyle \frac{m_A \times m_C}{4 \pi μ_0 r^2} \\ \\ &= \displaystyle \frac{1×10^{-4} \times 1×10^{-4} }{4 \pi \times 4 \pi×10^{-7} \times 2^2 } \\ \\ &= 1.583 \ \rm N \end{align} \)
磁極 \(A\) はN極,磁極 \(C\) はS極であるから,磁極間にはたらく力の種類は引力となり、下図のようになります。
2つの磁力の合成した力を求める
磁極 \(A \) にはたらく磁力を全て問の図に書き入れると以下のようになります。
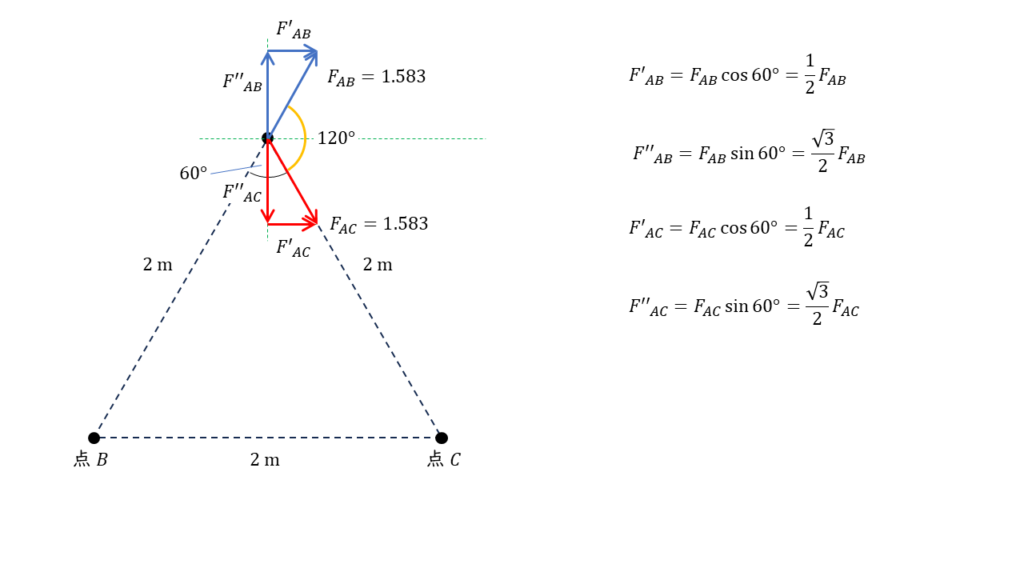
2つ磁力の合力を求めるために,2つ磁力それぞれ横方向と上下方向の力の成分に分解します。
磁力 \(F_{AB}\) の分解
横方向:\( F’_{AB} = F_{AB} \times \cos 60°= \displaystyle \frac{1}{2} F_{AB} \)
上下方向:\( F”_{AB} = F_{AB} \times \sin 60° = \displaystyle \frac{\sqrt{3}}{2} F_{AB} \)
磁力 \(F_{AC}\) の分解
横方向:\( F’_{AC} = F_{AC} \times \cos 60°= \displaystyle \frac{1}{2} F_{AC} \)
上下方向:\( F”_{AC} = F_{AC} \times \sin 60° = \displaystyle \frac{\sqrt{3}}{2} F_{AC} \)
各成分ごとに力の合計を求める
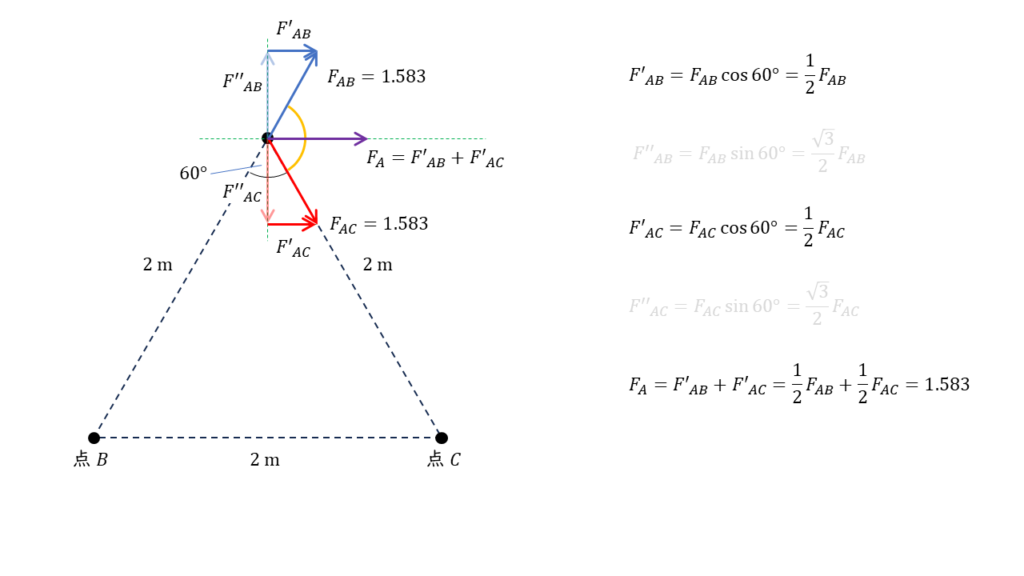
横方向:2つの力のベクトルは同じ方向を向いているため,各成分の足し算で合計の大きさを求めることができます。
\( \begin{align} F_x &= F’_{AB} + F’_{AC} \\ \\ &= \displaystyle \frac{1}{2} F_{AB} + \displaystyle \frac{1}{2} F_{AC} \\ \\ &= \displaystyle \frac{1}{2} \times 1.583 + \displaystyle \frac{1}{2} \times 1.583 \\ \\ &= 1.583 \end{align} \)
上下方向:2つの力のベクトルはそれぞれ反対方向を向いているため,各成分の引き算によって求めることができます。
\( \begin{align} F_x &= F”_{AB} – F”_{AC} \\ \\ &= \displaystyle \frac{\sqrt{3}}{2} F_{AB} – \displaystyle \frac{\sqrt{3}}{2} F_{AC} \\ \\ &= \displaystyle \frac{\sqrt{3}}{2} \times 1.583 – \displaystyle \frac{\sqrt{3}}{2} \times 1.583 \\ \\ &= 0 \end{align} \)
したがって,磁力の合力は以下の図ようになり、答えは(4)となります。











コメント