問題
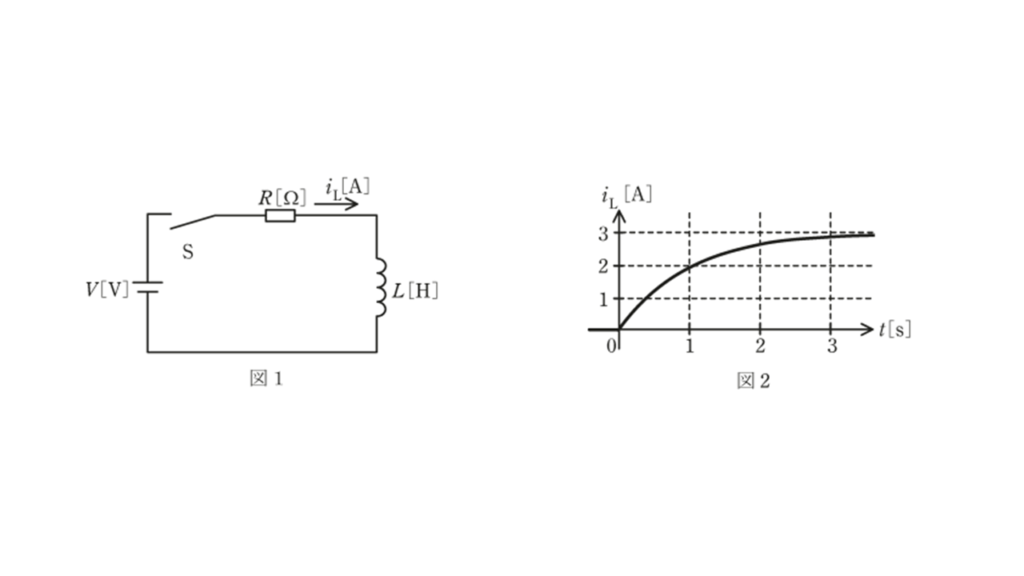
開放電圧が \(V\ \rm [V]\) で出力抵抗が十分に低い直流電圧源と,インダクタンスが \(L\ \rm[H]\) のコイルが与えられ,抵抗 \(R\ \rm[Ω]\) が図1のようにスイッチ \(S\) を介して接続されている。時刻\( t = 0\) でスイッチ \(S\) を閉じ,コイルの電流 \(i_L \ \rm [A]\) の時間に対する変化を計測して,波形として表す。 \(R = 1\ \rm \Omega\) としたところ,波形が図2であったとする。 \( R = 2\ \rm \Omega\) であればどのような波形となるか,波形の変化を最も適切に表すものを次の(1)~(5)のうちから一つ選べ。
ただし,選択肢の図中の点線は図2と同じ波形を表し,実線は \(R=2\ \rm \Omega\) のときの波形を表している。

解説
答え:(4)
抵抗-コイルを含む回路の電流を表す式を求める
回路を流れる電流を \(i_{(t)} \ \rm[A]\) ,コイルに印加される電圧を \(v_L \ \rm[V]\) ,抵抗に印加される電圧を \( v_r \ \rm[V]\) とすると,キルヒホッフの電圧の法則より
\( V = R i_{(t)} + L \displaystyle \frac{di_{(t)} }{dt} \)
と表すことができます。この式をラプラス変換すると,
\( \displaystyle \frac{V}{s} = RI_{(s)} + L \left( sI_{(s)} – i_{(0)} \right) \)
電流の初期値 \( i_{(0)} \) は,スイッチを閉じていないので,\(0 \ \rm A\)と考えることができます。
電流 \(I_{(s)}\) イコールの形に式変形すると,
\(\begin{align} \displaystyle \frac{V}{s} &= RI_{(s)} + sLI_{(s)} \\ \\ I_{(s)} &= \displaystyle \frac{V}{s \left( R + sL \right)} \\ \\ &= \displaystyle \frac{V}{R} \left( \displaystyle \frac{1}{s} – \displaystyle \frac{1}{s+\displaystyle \frac{R}{L}} \right) \end{align} \)
この式を逆ラプラス変換すると,
\( i_{(t)} = \displaystyle \frac{V}{R} \left( 1 – e^{- \frac{R}{L}t} \right) \)
となります。
重要公式は,
時間 \(t = 0 s\)のとき,最小となります。
\( i_{(0)} = \displaystyle \frac{V}{R} \left( 1 – e^0\right) =\displaystyle \frac{V}{R} \left( 1 – 1 \right) =0 \)
また,時間\( t = \infty\) のとき,最大となります。
\( i_{(\infty)} = \displaystyle \frac{V}{R} \left( 1 – e^{-\infty} \right) =\displaystyle \frac{V}{R} \left( 1 – 0 \right) = \displaystyle \frac{V}{R} \)

公式から抵抗値を変えた場合のグラフの形を考える
重要公式より,抵抗の値を \( R=1\) とした場合と, \(R=2\) とした場合の最終値の値を計算すると,
【\(R=1\)の場合】
\(\begin{align} i_{(t)} &= \displaystyle \frac{V}{R} \left( 1 – e^{- \frac{R}{L}t} \right) \\ &= \displaystyle \frac{V}{1} \left(1-0\right) \\ &= V \end{align} \)
【\(R=2\)の場合】
\(\begin{align} i_{(t)} &= \displaystyle \frac{V}{R} \left( 1 – e^{- \frac{R}{L}t} \right) \\ &= \displaystyle \frac{V}{2} \left(1-0\right) \\ &= \displaystyle \frac{V}{2} \end{align} \)
抵抗が大きくなると最終値が小さくなることが分かります。
また、指数部分 \( e^{- \frac{R}{L}t} \) に関して,抵抗 \(R\) の値が大きいほど,マイナス無限大に近づくまでの時間が速くなるため,グラフが平たんになるまでの時間も早まると考えることができます。
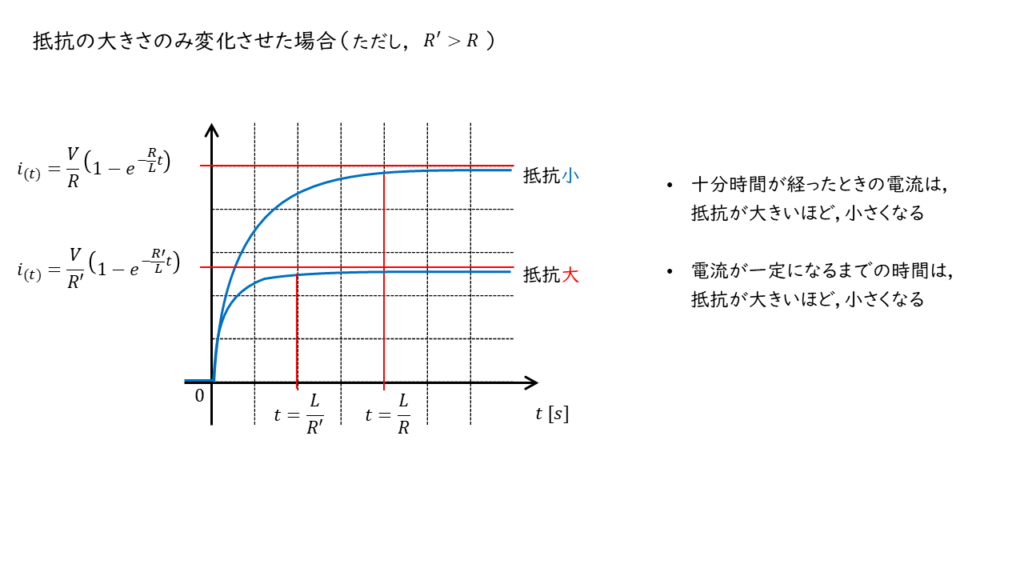
したがって,この条件に当てはまるグラフ選択肢の中では,(4)となります。











コメント