問題
図の回路において,スイッチ \(S\) が開いているとき,静電容量 \(C_1 = 4\ \rm mF\) のコンデンサには電荷 \(Q_1 = 0.3\ \rm C\) が蓄積されており,静電容量 \(C_2 = 2\ \rm mF\) のコンデンサの電荷は \(Q_2 = 0\ \rm C\) である。この状態でスイッチ \(S\) を閉じて,それから時間が十分に経過して過渡現象が終了した。この間に抵抗 \(R\ \rm [\Omega] \) で消費された電気エネルギー \(\rm [J]\) の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
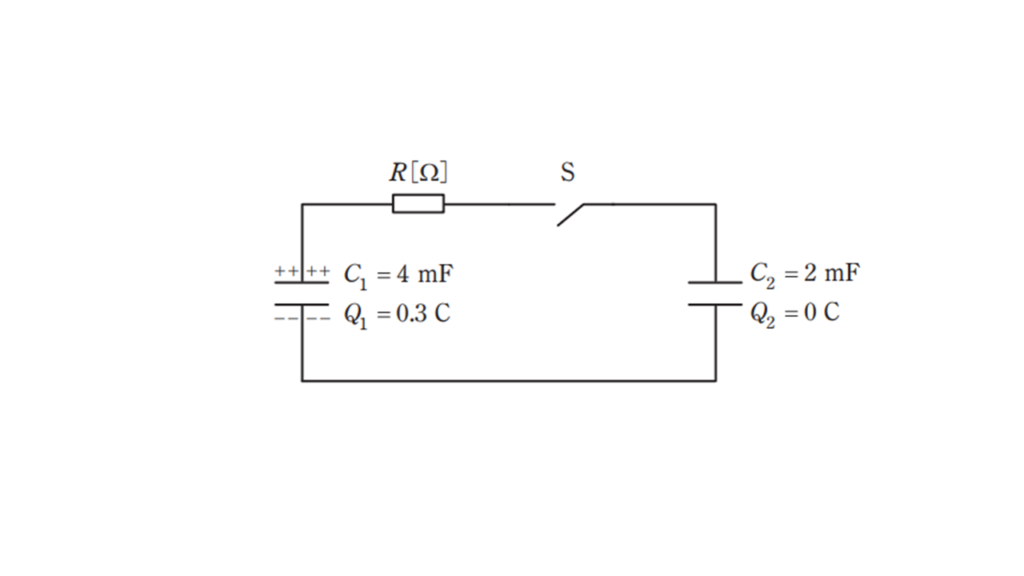
(1) \(1.25\) (2) \(2.50\) (3) \(3.75\) (4) \(5.63\) (5) \(7.50\)
解説
答え:(3)
スイッチ \(S\) を閉じる前のコンデンサに蓄えられているエネルギーを計算する
静電容量 \(C_1\) のコンデンサには,\(0.3\ \rm[C]\) の電荷が蓄えられており,もう一方の静電容量 \(C_2\) のコンデンサは,電荷が蓄えられていない状態です。
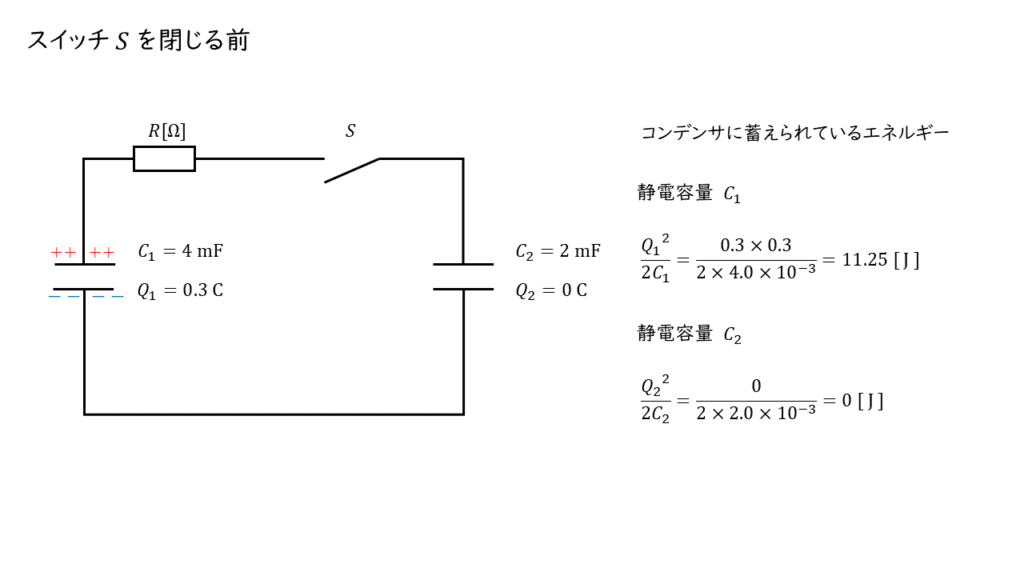
したがって,スイッチ \(S\) を閉じる前は, 静電容量 \(C_1\) のコンデンサが持つ静電エネルギーが回路全体のエネルギーとなります。
この時のエネルギーの大きさ\(W_1\ \rm[J]\) は,
\(\begin{align} W_1 &= \displaystyle \frac{Q^2}{2C} \\ \\ &= \displaystyle \frac{0.3^2}{2 \times 4 \times 10^{-3}} \\ \\ &= 11.25\ \rm[J] \end{align} \)
スイッチ \(S\) を閉じ,十分時間が経ったときのコンデンサに蓄えられているエネルギーを計算する
スイッチ \(S\) を閉じると,初めは2つのコンデンサの間に電位差があるため,電荷が移動します。
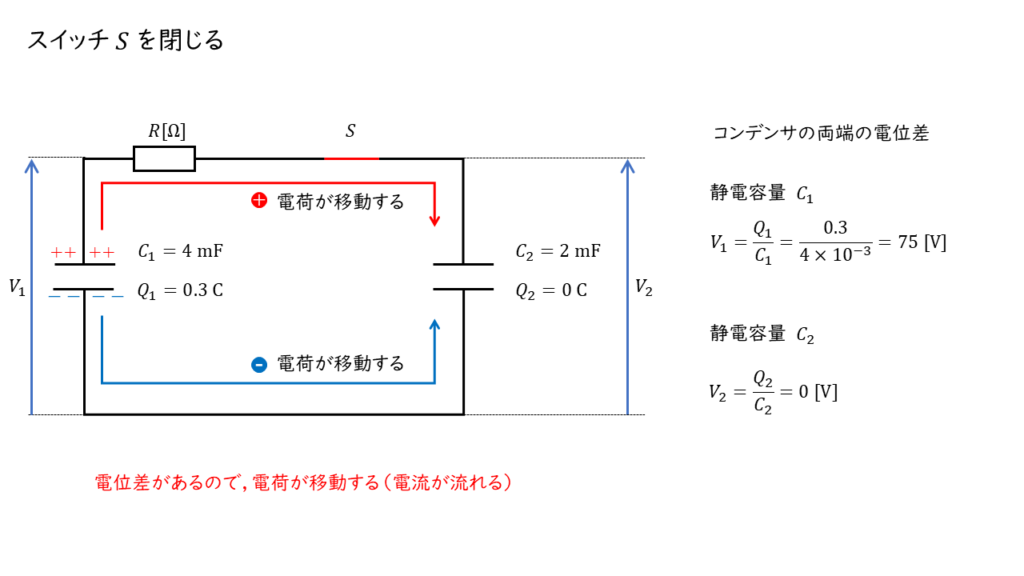
スイッチ \(S\) を閉じ,十分時間が経つと,2つのコンデンサの電位差がゼロになり,電荷の移動がなくなります。
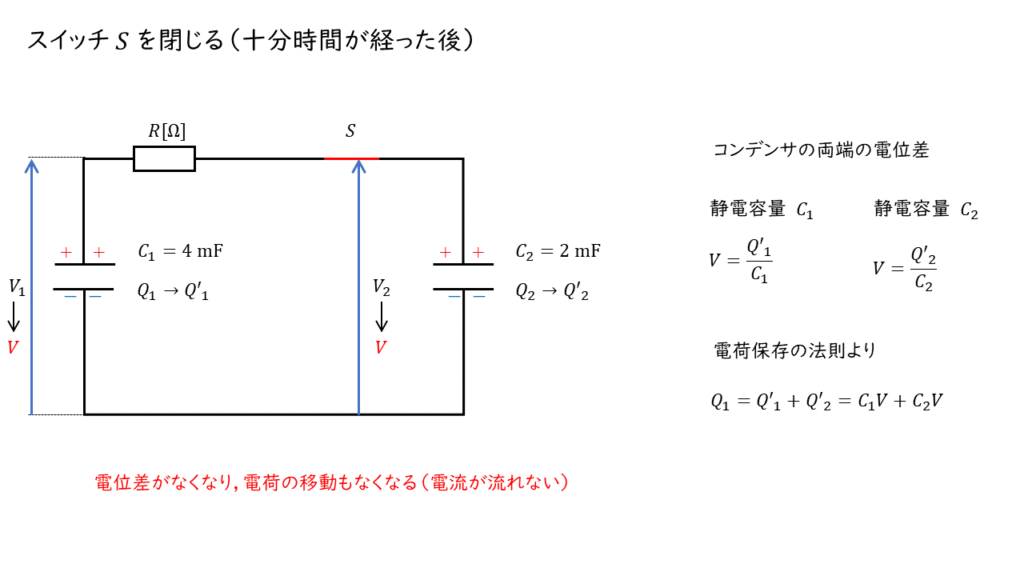
この時,それぞれのコンデンサの持つ電荷を\( Q’_1\) ,\(Q’_2\),コンデンサの極板間の電位差を\(V\ \rm[V]\)とすると,
\(Q’_1 = C_1 V\)
\(Q’_2 = C_2 V\)
\(\begin{align} Q_1 + Q_2 &= Q’_1 +Q’_2 \\ \\ 0.3 + 0 &= C_1 V +C_2 V \\ \\ 0.3 &= \left( 4.0 \times10^{-3} + 2.0 \times 10{-3} \right)V \\ \\ V &= \displaystyle \frac{0.3}{6.0 \times 10^{-3}} \\ \\ V &= 50 \end{align} \)
この条件から,スイッチ \(S\) を閉じた後のコンデンサに蓄えられているエネルギーの大きさ\(W_2\ \rm [J]\) を計算すると,
\(\begin{align} W_2 &= \displaystyle \frac{1}{2}C_1V^2 + \displaystyle \frac{1}{2}C_2V^2 \\ &= \displaystyle \frac{1}{2} \times \left( 4.0 \times 10^{-3} + 2.0 \times 10^{-3} \right) \times 50^2 \\ &= 7.5\ \rm [J] \end{align} \)
スイッチを閉じる前後の差から抵抗で消費されたエネルギーを求める
抵抗で消費されるエネルギーを \(W_r \ \rm[J] \)とすると,エネルギー保存の法則より,
\(\begin{align} W_1 &= W_2 +W_r \\ 11.25 &= 7.5 +W_r \\ W_r = 11.25-7.5= 3.75 \ \rm[J] \end{align} \)
よって,スイッチ \(S\) を閉じることによって,抵抗で消費されたエネルギーの大きさは,\(3.75\ \rm [J]\) と求めることができます。











コメント