【過去問解説】H27理論　問5　ソレノイドの誘導起電力に関する問題

誘導起電力の最大値の導出

問いのような三角形のソレノイドの内部を貫く磁束の数が時間と伴に変化していくときの，誘導起電力の最大値の導出について解説します。

微分を理解していないと難しい内容なので，読み飛ばしても構いません。

誘導起電力 \(e_\left( t \right) \)は，単位時間当たりのソレノイド内部の磁束の変化によって求めることができるので，

\( e _\left( t \right) = – \displaystyle \frac{\delta \phi }{\delta t} \)

と表すことができます。ここで，ソレノイドを貫く磁束の変化量 \( \delta \phi\) は，時間当たりの面積の変化量 \(\delta S\) と，磁束密度 \(B\) を用いて

\( \delta \phi = B \times \delta S\)

となります。したがって，誘導起電力の式は，

\( e_ \left( t \right) = – \displaystyle \frac{\delta \phi }{\delta t} = -B\displaystyle \frac{\delta S}{\delta t} \tag{1} \)

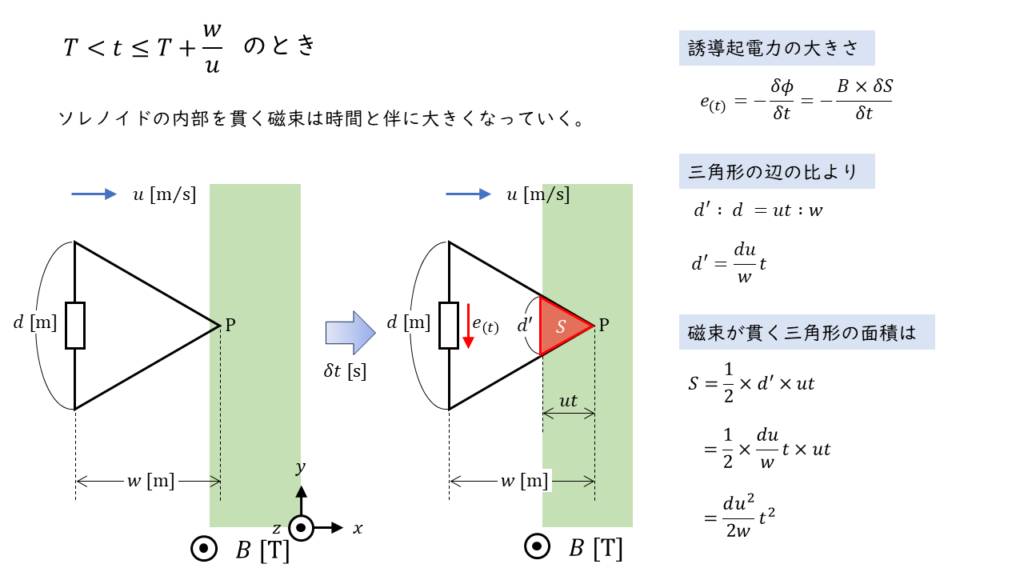
次に，磁界中にあるソレノイドの面積 \(S\) の大きさを，問題文中のソレノイド1辺の長さ \(d\) ，ソレノイドの高さ \(w\) ，ソレノイドの移動速度 \(u\) を用いて表すと，

\( \begin{align} S &= \displaystyle \frac{1}{2} \times d’ \times ut \\ \\ &= \displaystyle \frac{1}{2} \times \displaystyle \frac{d}{w}ut \times ut \\ \\ &= \displaystyle \frac{du^2}{2w}t^2 \tag{2} \end{align} \)

となります。式(2)を誘導起電力の式(1)に代入すると，

\( \begin{align} e_\left( t \right) &= -B\displaystyle \frac{\delta S}{\delta t} \\ \\ &= -B \displaystyle \frac{\delta}{\delta t} \times \displaystyle \frac{du^2}{2w}t^2 \\ \\ &= -\displaystyle \frac{Bdu^2}{2w} \times \displaystyle \frac{\delta}{\delta t} t^2 \end{align} \)

ここで，\( \displaystyle \frac{\delta}{\delta t} t^2 \) は， \(t^2\) を \(t\) で1回微分することを表しているので，

\( \begin{align} e_\left( t \right) &=-\displaystyle \frac{Bdu^2}{2w} \times \displaystyle \frac{\delta}{\delta t} t^2 \\ \\ &= -\displaystyle \frac{Bdu^2}{2w} \times 2t \\ \\ &= -\displaystyle \frac{Bdu^2}{w}t \end{align} \)

となります。問いの図より，ソレノイドを貫く磁束が最大となるときの時間は，\( t = T + \displaystyle \frac{v}{w} \) であるから，

\( \begin{align} e_\left( t \right) &= -\displaystyle \frac{Bdu^2}{w} \times \left( T + \displaystyle \frac{w}{u} \right) \\ \\ &= -\displaystyle \frac{Bdu^2}{w}T -\displaystyle \frac{Bdu^2}{w} \times \displaystyle \frac{w}{u} \\ \\ &= 0 – Bdu = -Bud \end{align} \)

以上の計算することができるので，ソレノイドを移動させたときの誘導起電力の最大値は，

\( e_ \left(t\right) = -Bud \)

となります。